Rang (statistiek)

In dit artikel leggen we uit wat bereik in statistieken is en hoe dit wordt berekend. U vindt een opgeloste oefening over de reikwijdte van een dataset en tot slot laten we u zien waarvoor deze dient en wanneer deze moet worden gebruikt.

Wat is bereik in statistieken?

In de statistiek is bereik een maatstaf voor de spreiding die het verschil aangeeft tussen de maximale waarde en de minimale waarde van de gegevens van een monster. Om de omvang van een populatie of statistische steekproef te berekenen, moet daarom de maximale waarde worden afgetrokken van de minimumwaarde.

Als de maximale waarde van een dataset bijvoorbeeld 9 is en de minimumwaarde 2, is het bereik van deze statistische steekproef 7 (9-2=7).

Het statistische bereik wordt ook wel de omvang of het meetbereik genoemd.

Het bereik is dus een maatstaf voor de spreiding met variantie, standaardafwijking (of standaardafwijking), gemiddelde afwijking en variatiecoëfficiënt.

Hoe bereik in statistieken te berekenen

Het bereik van een steekproef wordt berekend door de extreme waarden van de statistische steekproefgegevens af te trekken, dat wil zeggen dat het bereik van een steekproef gelijk is aan de maximale waarde van alle gegevens minus de minimumwaarde .

Daarom is de formule voor het berekenen van het statistische bereik van een dataset:

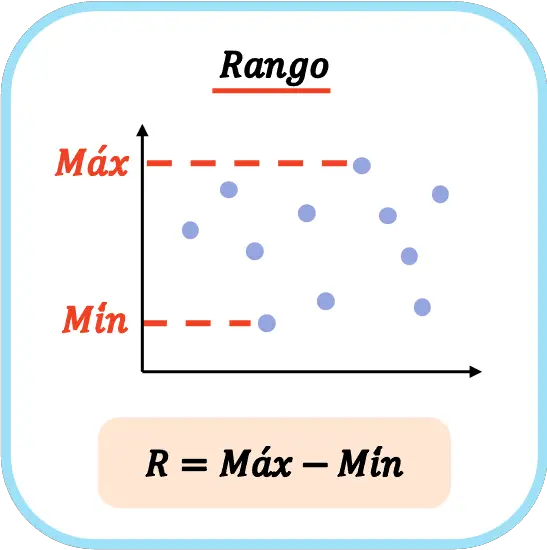
In de statistieken wordt het symbool voor een hoofdletter R vaak gebruikt om de omvang van een gegevensreeks aan te duiden.

Het berekenen van het bereik van een dataset is dus vrij eenvoudig, omdat je alleen maar het verschil tussen de extreme waarden hoeft te bepalen. Het enige waar u op hoeft te letten is het correct krijgen van de maximale en minimale gegevens en het niet vergeten van cijfers.

Voorbeeldbereik (statistiek)

Nadat u de definitie van bereik in de statistieken heeft gezien, vindt u hieronder een uitgewerkt voorbeeld, zodat u kunt zien hoe het bereik van een dataset wordt verkregen.

• Een bedrijf wil de omzet van zijn vlaggenschipproduct de afgelopen twintig jaar statistisch analyseren. Om dit te doen, vragen ze u om verschillende statistische metingen te berekenen, waaronder de rangschikking. Als de verkoop van het product is zoals weergegeven in de volgende tabel, wat is dan het bereik van deze dataset?

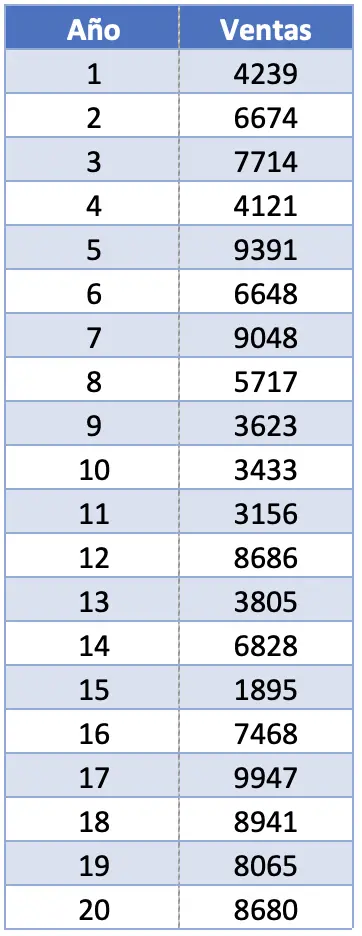
In deze oefening hebben we 20 observaties. In werkelijkheid maakt het totale aantal waarnemingen geen verschil bij het berekenen van de omvang van een steekproef, omdat we alleen geïnteresseerd zijn in de grootste waarde en de kleinste waarde.

We moeten daarom de bovenstaande formule gebruiken om de omvang van deze statistische steekproef te bepalen.

De maximale waarde van het interval is 9947 verkochte eenheden en de minimale waarde is 1895. Daarom moeten we deze twee waarden aftrekken om het bereik van de dataset te vinden:

Dit betekent dat de maximale omzetmutatie over de afgelopen jaren 8.052 eenheden bedraagt. Hieronder kunt u grafisch alle trainingsgegevens zien, samen met het statistische bereik. De grafiek zal u waarschijnlijk helpen de betekenis van het bereik te begrijpen.

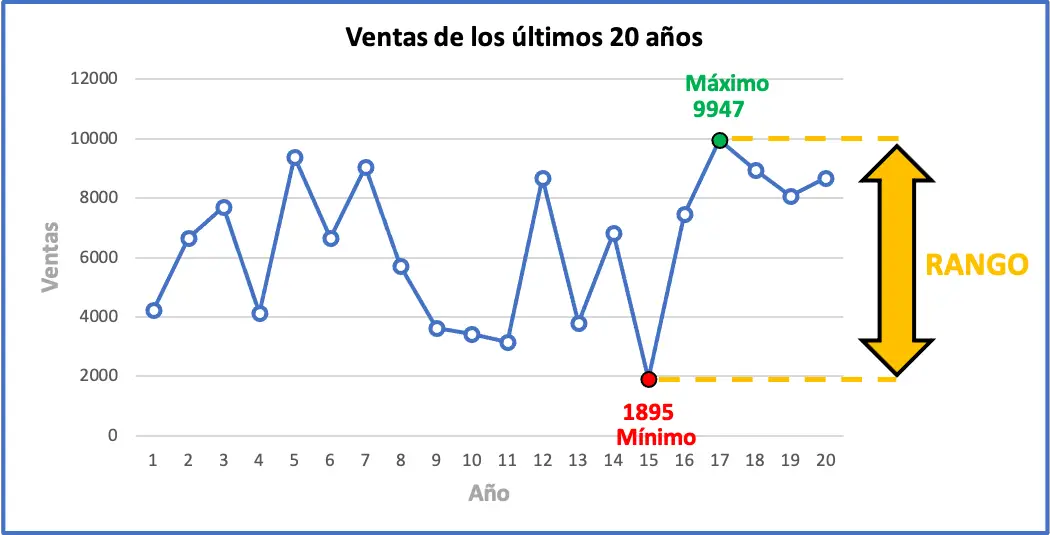
Waar wordt het statistische bereik voor gebruikt?

Om het begrip omvang in de statistiek verder te begrijpen, zullen we zien waarvoor het wordt gebruikt en hoe we deze maatstaf voor spreiding kunnen interpreteren.

In statistieken toont bereik het verschil tussen de maximale waarde en de minimale waarde van een dataset. Daarom is bereik een maatstaf die wordt gebruikt om de totale spreiding van een dataset aan te geven .

Als je de bereikwaarde van een dataset kent, weet je het maximale verschil tussen twee willekeurige waarnemingen in die set, zodat je een idee kunt krijgen of de gegevens verspreid zijn of dicht bij elkaar liggen. Over het algemeen is het voordelig als het bereik zo minimaal mogelijk is, omdat er dan weinig spreiding is en de berekeningen daardoor nauwkeuriger zullen zijn.

Het bereik kan bijvoorbeeld een meting zijn die een vergelijking tussen twee verschillende monsters mogelijk maakt, omdat u hierdoor een idee krijgt van de spreiding van de monsters.

Er moet echter voorzichtigheid worden betracht bij het interpreteren van het statistische bereik, aangezien dit misleidend kan zijn. Het kan zijn dat een dataset feitelijk een zeer lage spreiding heeft, maar als er een uitschieter binnen de steekproef aanwezig is, zal het bereik zeer breed zijn en daarom de spreiding van de steekproef niet goed weerspiegelen.

Bovendien is het niet hetzelfde dat een steekproef waarvan de waarden in de orde van tientallen liggen, een rangorde van 5 heeft, als een steekproef waarvan de waarden in de orde van duizenden liggen, dezelfde rangorde heeft. Logischerwijs is het eerste monster, zelfs als beide bereiken hetzelfde nummer hebben, veel meer verspreid dan het tweede.

Concluderend is bereik een nuttige statistische maatstaf voor het analyseren van de spreiding van een dataset, maar om de gegevens correct te interpreteren moeten ook andere statistieken worden berekend.