Statistische formules

Von Dr.benjamin anderson August 1, 2023 Statistieken Keine Kommentare

Hier vindt u de belangrijkste statistische formules. We laten u ook gekoppeld aan onze artikelen waarin u voorbeelden van de toepassing van elke statistische formule kunt zien en bovendien kunt u een online rekenmachine gebruiken, zodat u de berekeningen niet hoeft uit te voeren en het resultaat van de formule direct kent.

Formules voor statistische metingen van centrale tendens

Half

Om het gemiddelde te berekenen, telt u alle waarden bij elkaar op en deelt u deze door het totale aantal gegevens. De formule voor het gemiddelde is daarom als volgt:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}$

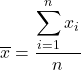
In de statistiek wordt het gemiddelde ook wel het rekenkundig gemiddelde of gemiddelde genoemd.

➤ Zie: Rekenkundige gemiddelde rekenmachine

Mediaan

De mediaan is de middelste waarde van alle gegevens, gerangschikt van klein naar groot. Met andere woorden: de mediaan verdeelt de geordende dataset in twee gelijke delen.

De berekening van de mediaan hangt af van het feit of het totale aantal gegevens even of oneven is:

Als het totale aantal gegevens oneven is, is de mediaan de waarde die precies in het midden van de gegevens valt. Dat wil zeggen de waarde die zich op positie (n+1)/2 van de gesorteerde gegevens bevindt.

$Me=x_{\frac{n+1}{2}$

Als het totale aantal gegevenspunten even is, is de mediaan het gemiddelde van de twee gegevenspunten in het midden. Dat wil zeggen het rekenkundig gemiddelde van de waarden die gevonden worden op posities n/2 en n/2+1 van de geordende data.

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

Goud

$n$

is het totale aantal gegevens in de steekproef en het symbool Me geeft de mediaan aan.

➤ Zie: Mediaancalculator

Mode

In de statistiek is de modus de waarde in de dataset die de hoogste absolute frequentie heeft, dat wil zeggen dat de modus de meest herhaalde waarde in een dataset is.

Daarom is er geen specifieke formule voor de modus, maar om de modus van een statistische gegevensset te berekenen, telt u eenvoudigweg het aantal keren dat elk gegevenselement in de steekproef voorkomt, en de gegevens die het meest worden herhaald, zullen de modus zijn.

Er kan ook worden gezegd dat de modus een statistische modus of modale waarde is.

➤ Zie: Modecalculator

Formules voor statistische metingen van spreiding

Standaardafwijking

De standaarddeviatie, ook wel de standaarddeviatie genoemd, is gelijk aan de vierkantswortel van de som van de kwadraten van de afwijkingen van de gegevensreeks gedeeld door het totale aantal waarnemingen.

Daarom is de formule voor standaarddeviatie :

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n}}$

➤ Zie: Standaarddeviatiecalculator

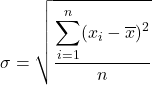
Variantie

De variantie is gelijk aan de som van de kwadraten van de residuen over het totale aantal waarnemingen. De formule voor deze statistische metriek is daarom als volgt:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}$

Goud:

$X$

is de willekeurige variabele waarvoor u de variantie wilt berekenen.
$x_i$

is de gegevenswaarde

$i$

.
$n$

is het totale aantal waarnemingen.
$\overline{X}$

is het gemiddelde van de willekeurige variabele

$X$

.

➤ Zie: Gatcalculator

Variatiecoëfficiënt

In de statistiek is de variatiecoëfficiënt een maatstaf voor de spreiding die wordt gebruikt om de spreiding van een gegevensset ten opzichte van het gemiddelde te bepalen. De variatiecoëfficiënt wordt berekend door de standaarddeviatie van de gegevens te delen door het gemiddelde en vervolgens te vermenigvuldigen met 100 om de waarde als een percentage uit te drukken.

$CV=\cfrac{\sigma}{\overline{x}}\cdot 100$

➤ Zie: Variatiecoëfficiëntcalculator

Netjes

Statistisch bereik is een spreidingsmaatstaf die het verschil aangeeft tussen de maximale waarde en de minimale waarde van gegevens in een steekproef. Om de omvang van een populatie of statistische steekproef te berekenen, moet daarom de maximale waarde worden afgetrokken van de minimumwaarde.

$R=\text{M\'ax}-\text{M\'in}$

➤ Zie: Voorbeeld van statistisch bereik

Interkwartielbereik

Het interkwartielbereik , ook wel interkwartielbereik genoemd, is een maatstaf voor de statistische spreiding die het verschil tussen het derde en eerste kwartiel aangeeft.

Om het interkwartielbereik van een statistische dataset te berekenen, moet u daarom eerst het derde en eerste kwartiel vinden en deze vervolgens aftrekken.

$IQR=Q_3-Q_1$

➤ Zie: Interkwartielbereikcalculator

gemiddeld verschil

De gemiddelde afwijking , ook wel de gemiddelde absolute afwijking genoemd, is het gemiddelde van de absolute afwijkingen. De gemiddelde afwijking is daarom gelijk aan de som van de afwijkingen van elk gegevensitem van het rekenkundig gemiddelde gedeeld door het totale aantal gegevensitems.

$D_{\overline{x}}=\cfrac{\sum_{i=1}^n|x_i-\overline{x}|}{n}$

➤ Zie: Berekening van de gemiddelde afwijking

Formules voor statistische positiemetingen

kwartielen

In de statistieken zijn kwartielen de drie waarden die een reeks geordende gegevens in vier gelijke delen verdelen. Het eerste, tweede en derde kwartiel vertegenwoordigen dus respectievelijk 25%, 50% en 75% van alle statistische gegevens.

Kwartielen worden weergegeven door een hoofdletter Q en de kwartielindex, dus het eerste kwartiel is Q ₁ , het tweede kwartiel is Q ₂ en het derde kwartiel is Q ₃ .

De kwartielformule is:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

Let op: deze formule vertelt ons de positie van het kwartiel, niet de waarde van het kwartiel. Het kwartiel zijn de gegevens die zich bevinden op de positie die door de formule wordt verkregen.

Soms geeft het resultaat van deze formule ons echter een decimaal getal. We moeten daarom twee gevallen onderscheiden, afhankelijk van of het resultaat een decimaal getal is of niet:

Als het resultaat van de formule een getal zonder decimaal deel is, zijn het kwartiel de gegevens die zich op de positie bevinden die door de bovenstaande formule wordt aangegeven.
Als het resultaat van de formule een getal met een decimaal deel is, wordt de kwartielwaarde berekend met behulp van de volgende formule:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

Waar x _i en x _i+1 de getallen zijn van de posities waartussen het getal verkregen door de eerste formule zich bevindt, en d het decimale deel is van het getal verkregen door de eerste formule.

➤ Zie: Kwartielcalculator

decielen

In de statistieken zijn decielen de negen waarden die een reeks geordende gegevens in tien gelijke delen verdelen. Zodat het eerste, tweede, derde,… deciel 10%, 20%, 30%,… van de steekproef of populatie vertegenwoordigt.

Decielen worden weergegeven door de hoofdletter D en de decielindex, dat wil zeggen, het eerste deciel is D ₁ , het tweede deciel is D ₂ , het derde deciel is D ₃ , enz.

De decielformule is als volgt:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

Let op: deze formule vertelt ons de positie van het deciel, niet de waarde van het deciel. Het deciel bestaat uit de gegevens die zich bevinden op de positie die door de formule wordt verkregen.

Soms geeft het resultaat van deze formule ons echter een decimaal getal. We moeten daarom twee gevallen onderscheiden, afhankelijk van of het resultaat een decimaal getal is of niet:

Als het resultaat van de formule een getal is zonder een decimaal deel , bestaat het deciel uit de gegevens die zich bevinden op de positie die wordt geboden door de bovenstaande formule.
Als het resultaat van de formule een getal met een decimaal deel is, wordt de decielwaarde berekend met behulp van de volgende formule:

$D=x_i+d\cdot (x_{i+1}-x_i)$

Waar x _i en x _i+1 de getallen zijn van de posities waartussen het getal verkregen door de eerste formule zich bevindt, en d het decimale deel is van het getal verkregen door de eerste formule.

➤ Zie: Decielcalculator

percentielen

In de statistieken zijn percentielen de waarden die een reeks geordende gegevens in honderd gelijke delen verdelen. Een percentiel geeft dus de waarde aan waaronder een percentage van de dataset valt.

Percentielen worden weergegeven door de hoofdletter P en de percentielindex, dat wil zeggen dat het eerste percentiel P ₁ is, het 40e percentiel P ₄₀ , het 79e percentiel P ₇₉ , enz.

De percentielformule is:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Let op: deze formule vertelt ons de positie van het percentiel, maar niet de waarde ervan. Het percentiel bestaat uit de gegevens die zich bevinden op de positie die door de formule wordt verkregen.

Soms geeft het resultaat van deze formule ons echter een decimaal getal. We moeten daarom twee gevallen onderscheiden, afhankelijk van of het resultaat een decimaal getal is of niet:

Als het resultaat van de formule een getal zonder decimaal deel is, komt het percentiel overeen met de gegevens die zich in de positie bevinden die door de bovenstaande formule wordt verstrekt.
Als het resultaat van de formule een getal met een decimaal deel is, wordt de exacte percentielwaarde berekend met behulp van de volgende formule:

$P=x_i+d\cdot (x_{i+1}-x_i)$

Waar x _i en x _i+1 de getallen zijn van de posities waartussen het getal verkregen door de eerste formule zich bevindt, en d het decimale deel is van het getal verkregen door de eerste formule.

➤ Zie: Percentielcalculator

Statistische vormmetingsformules

asymmetriecoëfficiënt

De scheefheidscoëfficiënt, of scheefheidsindex, is een statistische coëfficiënt die wordt gebruikt om de scheefheid van een verdeling te bepalen. Door de asymmetriecoëfficiënt te berekenen, kunt u dus het type asymmetrie van de verdeling kennen zonder dat u er een grafische weergave van hoeft te maken.

De formule voor de asymmetriecoëfficiënt is als volgt:

$\displaystyle\gamma_1=\frac{\overline{x}_3}{\sigma^3}$

Op equivalente wijze kan een van de volgende twee formules worden gebruikt om de Fisher-asymmetriecoëfficiënt te berekenen:

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\overline{x}\right)^3}{n\cdot \sigma ^3}$

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\cdot \overline{x}\cdot \sigma^2 - \overline{x}^3}{\sigma^3}$

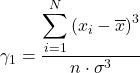
Goud

$E$

is de wiskundige verwachting,

$\overline{x}$

het rekenkundig gemiddelde,

$\sigma$

de standaarddeviatie en

$n$

het totale aantal gegevens.

➤ Zie: Asymmetriecoëfficiënt

kurtosis-coëfficiënt

Kurtosis, ook wel scherpte genoemd, geeft aan hoe geconcentreerd een verdeling rond het gemiddelde is. Met andere woorden, kurtosis geeft aan of een verdeling steil of vlak is. Concreet geldt: hoe groter de kurtosis van een verdeling, hoe steiler (of scherper) deze is.

De formule voor de kurtosis-coëfficiënt is als volgt:

$\displaystyle g_2=\frac{1}{n}\cdot\frac{\displaystyle \sum_{i=1}^n(x_i-\overline{x})^4}{\sigma^4}-3$

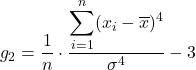
Goud

$x_i$

is de waarde die overeenkomt met de waarneming

$i$

$\overline{x}$

het rekenkundig gemiddelde,

$\sigma$

de standaarddeviatie en

$n$

het totale aantal gegevens.

➤ Zie: Afvlakkingscoëfficiëntcalculator

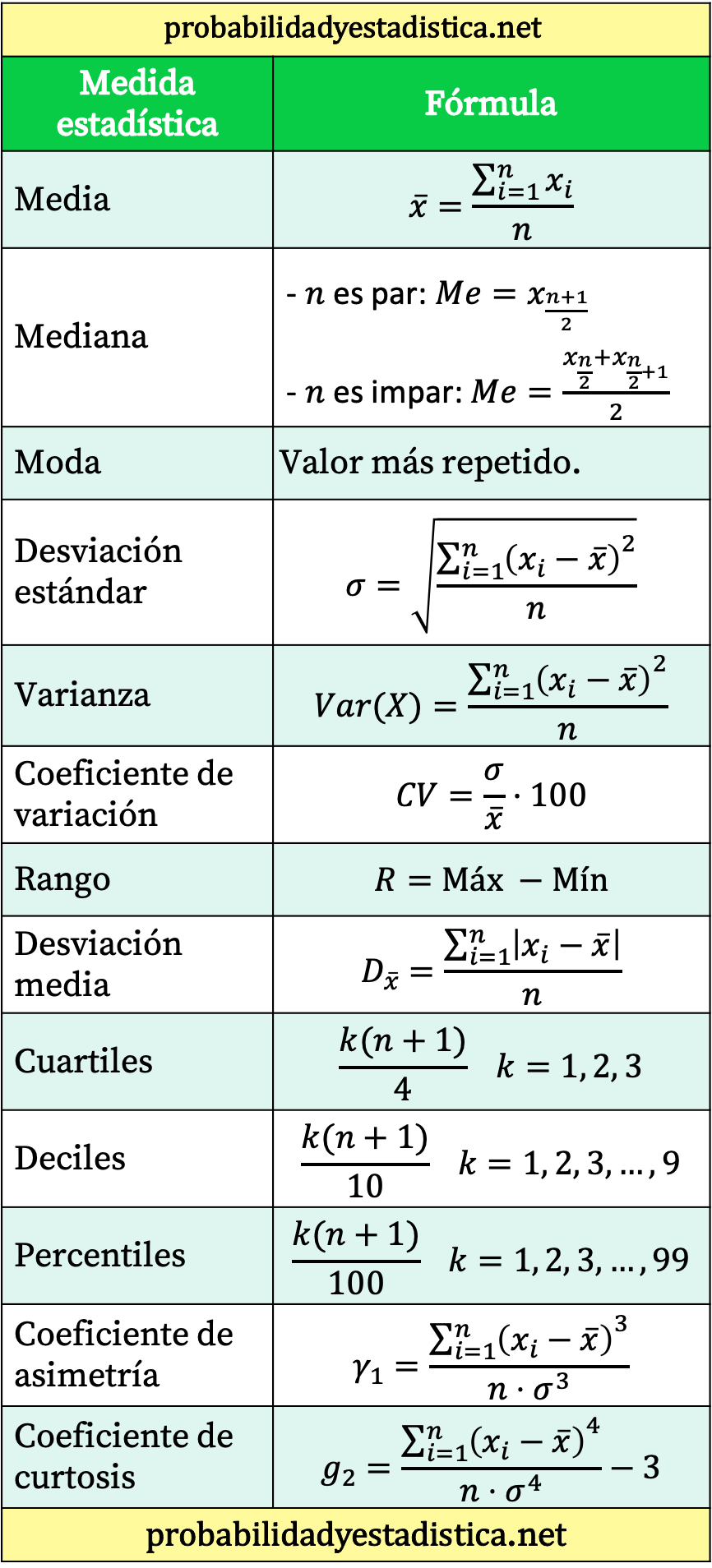
Overzichtstabel van alle statistische formules

Ten slotte laten we u een tabel achter die de belangrijkste statistische formules samenvat.

➤ Zie: Waarschijnlijkheidsformules

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder

Formules voor statistische metingen van centrale tendens

Half

Mediaan

Mode

Formules voor statistische metingen van spreiding

Standaardafwijking

Variantie

Variatiecoëfficiënt

Netjes

Interkwartielbereik

gemiddeld verschil

Formules voor statistische positiemetingen

kwartielen

decielen

percentielen

Statistische vormmetingsformules

asymmetriecoëfficiënt

kurtosis-coëfficiënt

Overzichtstabel van alle statistische formules

Über den Autor

Dr.benjamin anderson

Einen Kommentar hinzufügen