Mode (statistieken)
In dit artikel wordt uitgelegd wat de modus in de statistieken is. U leert hoe u de statistische modus voor gegroepeerde gegevens en niet-gegroepeerde gegevens kunt vinden, de verschillende soorten modi en verschillende voorbeelden van deze statistische meting.
Wat is modus in de statistiek?
In de statistiek is de modus de waarde in de dataset die de hoogste absolute frequentie heeft, dat wil zeggen dat de modus de meest herhaalde waarde in een dataset is.
Om de modus van een statistische gegevensset te berekenen, telt u daarom eenvoudigweg het aantal keren dat elk gegevenselement in de steekproef voorkomt, en de meest herhaalde gegevens zullen de modus zijn.
De modus wordt gebruikt om een statistische verdeling te definiëren, aangezien de meest herhaalde waarde zich gewoonlijk in het midden van de verdeling bevindt.
Er kan ook worden gezegd dat de modus een statistische modus of modale waarde is. Op dezelfde manier, wanneer gegevens in intervallen worden gegroepeerd, is het meest herhaalde interval het modale interval of de modale klasse .
Over het algemeen wordt de term Mo gebruikt als symbool voor de statistische modus, de distributiemodus X is bijvoorbeeld Mo(X).
Houd er rekening mee dat de modus een statistische maatstaf is voor de middenpositie, maar ook voor de mediaan en het gemiddelde. Hieronder zullen we zien wat elk van deze statistische metingen betekent.
Modustypen in statistieken
In de statistieken zijn er verschillende soorten modi die worden geclassificeerd op basis van het aantal meest herhaalde waarden:
- Unimodale modus : er is slechts één waarde met het maximale aantal herhalingen. Bijvoorbeeld [1, 4, 2, 4, 5, 3].
- Bimodale modus : het maximale aantal herhalingen vindt plaats bij twee verschillende waarden, en beide waarden worden hetzelfde aantal keren herhaald. Bijvoorbeeld [2, 6, 7, 2, 3, 6, 9].
- Multimodale modus : Drie of meer waarden hebben hetzelfde maximale aantal herhalingen. Bijvoorbeeld [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1].
Hoe de statistische modus te vinden
Om de statistische modus van een dataset te vinden, moet u de volgende stappen volgen:
- Zet de gegevens op orde. Deze stap is niet verplicht, maar maakt het tellen van getallen eenvoudiger.
- Tel hoe vaak elk getal voorkomt.
- Het getal dat het vaakst verschijnt is de statistische modus.
Voorbeelden van statistische modus
Gezien de definitie van mode in de statistieken, ziet u hieronder een voorbeeld van elk type mode, zodat u het concept beter kunt begrijpen.
Voorbeeld van unimodale modus
- Wat is de modus van de volgende dataset?
![]()
De nummers zijn niet geordend, dus we zullen ze eerst ordenen om het gemakkelijker te maken de modus te vinden.
![]()
De nummers 2 en 9 verschijnen twee keer, maar het nummer 5 wordt drie keer herhaald. Daarom is de modus van de gegevensreeks nummer 5.
![]()
Voorbeeld van bimodale modus
- Bereken de modus van de volgende dataset:
![]()
![]()
Eerst zetten we de cijfers op volgorde:
![]()
![]()
Zoals je kunt zien, verschijnen het getal 6 en het getal 8 in totaal vier keer, wat het maximale aantal herhalingen is. Daarom is het in dit geval een bimodale modus en zijn de twee getallen de modus van de dataset:
![]()
Voorbeeld van multimodale modus
- Zoek de volgende datasetmodus:
![]()
![]()
![]()
Omdat er veel gegevens zijn, sorteren we deze eerst in oplopende volgorde om het tellen gemakkelijker te maken:
![]()
![]()
![]()
De meest herhaalde nummers zijn 20, 27 en 31, alle drie de nummers worden vijf keer herhaald. De modus van dit voorbeeld is daarom multimodaal.
![]()
mode rekenmachine
Voer gegevens uit een statistisch voorbeeld in de volgende online calculator in om de modus ervan te berekenen. Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.
Modus voor gegroepeerde gegevens
Als we gegevens in de vorm van intervallen hebben gegroepeerd, weten we niet echt hoe vaak elk stukje gegevens wordt herhaald; we kennen alleen de frequentie van elk interval.
Om de modus van gegevens gegroepeerd in intervallen te berekenen, moeten we dus de volgende formule gebruiken :
![]()
Goud:
- Li is de ondergrens van het modale interval (hoogste absolute frequentie-interval).
- fi is de absolute frequentie van het modale interval.
- f i-1 is de absolute frequentie van het interval vóór het modale.
- f i+1 is de absolute frequentie van het interval na het modale.
- A i is de breedte van het modale interval.
Als voorbeeld heb je hieronder een oefening opgelost waarin de modus van gegevens gegroepeerd in intervallen wordt berekend:
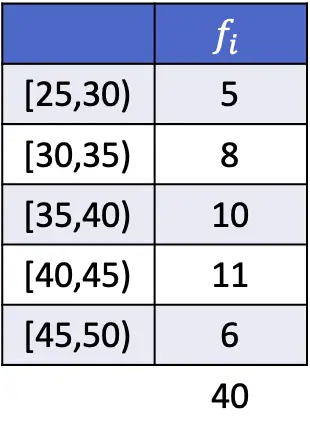
In dit geval is het modale interval [40,45), aangezien dit het interval is met de grootste absolute frequentie. Daarom zijn de modusformuleparameters voor gegroepeerde gegevens:
![Rendered by QuickLaTeX.com \begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-85aef7092d3e0c7769ad17b96aae294c_l3.png)
We passen daarom de formule toe om de modus van de gegevens te bepalen, gegroepeerd in intervallen, en we voeren de berekening uit:
![Rendered by QuickLaTeX.com \begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3ee33fdb43267fdcfc6d222ed6798fca_l3.png)
Verschil tussen modus, gemiddelde en mediaan
In dit laatste deel zullen we zien wat het verschil is tussen de modus, het gemiddelde en de mediaan. Omdat het alle drie statistische metingen van de centrale positie zijn, is hun betekenis verschillend.
Zoals in het hele artikel wordt uitgelegd, is de modus in de wiskunde de meest herhaalde waarde in een dataset.
Ten tweede is het gemiddelde de gemiddelde waarde van alle statistische gegevens. Om het gemiddelde van bepaalde gegevens te verkrijgen, moet u dus alle gegevens bij elkaar optellen en het resultaat delen door het aantal waarnemingen.
En ten slotte is de mediaan de waarde die centraal staat bij het ordenen van de gegevens.
De drie statistische maatstaven helpen dus bij het definiëren van een waarschijnlijkheidsverdeling, omdat ze een idee geven van de centrale waarden ervan. Maar houd er rekening mee dat er niet één maatstaf is die beter is dan de andere; er worden alleen maar verschillende concepten bedoeld.
Mode-eigenschappen
De mode-eigenschappen zijn:
- Modus kan worden gevonden in zowel kwantitatieve variabelen als kwalitatieve variabelen.
- Als we een lineaire transformatie toepassen op een willekeurige variabele, zal de waarde van het gemiddelde veranderen afhankelijk van de toegepaste bewerkingen.
- Over het algemeen is de modus ongevoelig voor uitbijters.
- Als alle waarden dezelfde frequentie hebben, is er geen modus.
![]()