Statistische populatie
In dit artikel leggen we uit wat statistische populatie is. Je zult verschillende voorbeelden vinden van statistische populaties, de verschillende soorten populaties die er bestaan en tot slot wat het verschil is tussen populatie en steekproef in statistieken.
Wat is een statistische populatie?
In de statistiek is een populatie een verzameling elementen met vergelijkbare kenmerken waarop een statistisch onderzoek moet worden uitgevoerd.
Dit concept kan door elkaar worden aangeduid als statistische populatie of eenvoudigweg populatie.
Vervolgens is de populatiegrootte , ook wel de populatiegrootte genoemd, het totale aantal elementen in de groep die je wilt bestuderen.
Voorbeelden van statistische populatie
Als we de definitie van statistische populatie in ogenschouw nemen, zullen we verschillende voorbeelden van populaties zien om de betekenis ervan beter te begrijpen.
Als we bijvoorbeeld een onderzoek doen naar de cijfers die leerlingen in een klas in de loop van een jaar hebben behaald, vormen de leerlingen in die klas de statistische populatie van het onderzoek.
Nog een voorbeeld: als je een statistische analyse wilt uitvoeren van de kwaliteit van onderdelen die in een fabriek gedurende een bepaalde periode zijn geproduceerd, vormen alle onderdelen die in deze periode door deze fabriek zijn geproduceerd de bestudeerde populatie.
Ten slotte vormen de inwoners van een gebied ook een statistische populatie wanneer er statistieken over dat grondgebied worden uitgevoerd, bijvoorbeeld bij het berekenen van de levensverwachting van een land vertegenwoordigen de inwoners van dit land de statistische populatie van het onderzoek.
Soorten statistische populatie
Er zijn twee soorten statistische populaties:
- Eindige statistische populatie : populatie waarvan het aantal elementen eindig is, dat wil zeggen dat ze kunnen worden geteld.
- Oneindige statistische populatie : populatie waarvan het aantal elementen oneindig is, dat wil zeggen die geen einde kent.
Het aantal auto’s dat gedurende een dag op een weg rijdt, vormt bijvoorbeeld een eindige populatie, aangezien het, ook al is het een zeer groot aantal, telbaar is. In plaats daarvan vormt het aantal planeten in het universum een oneindige populatie, omdat nog niet alle planeten ontdekt zijn en daarom niet kunnen worden geteld.
Houd er rekening mee dat er veel manieren zijn om statistische populatietypen te groeperen. Ze kunnen ook worden onderverdeeld in kwalitatieve populaties en kwantitatieve populaties op basis van hun variabele. Maar normaal gesproken wordt er een grote classificatie gemaakt tussen eindige populaties en oneindige populaties.
Statistische populatie en steekproef
Ten slotte zullen we zien hoe de begrippen populatie en steekproef in de statistiek verschillen, aangezien het twee termen zijn die doorgaans hand in hand gaan.
In de statistiek is het verschil tussen populatie en steekproef de verhouding ten opzichte van het totale aantal elementen in het onderzoek. De statistische populatie omvat alle elementen waarop het onderzoek wordt uitgevoerd, maar de statistische steekproef maakt deel uit van alle elementen van het onderzoek.
De omvang van een steekproef zal daarom altijd kleiner zijn dan of gelijk zijn aan de omvang van een populatie.
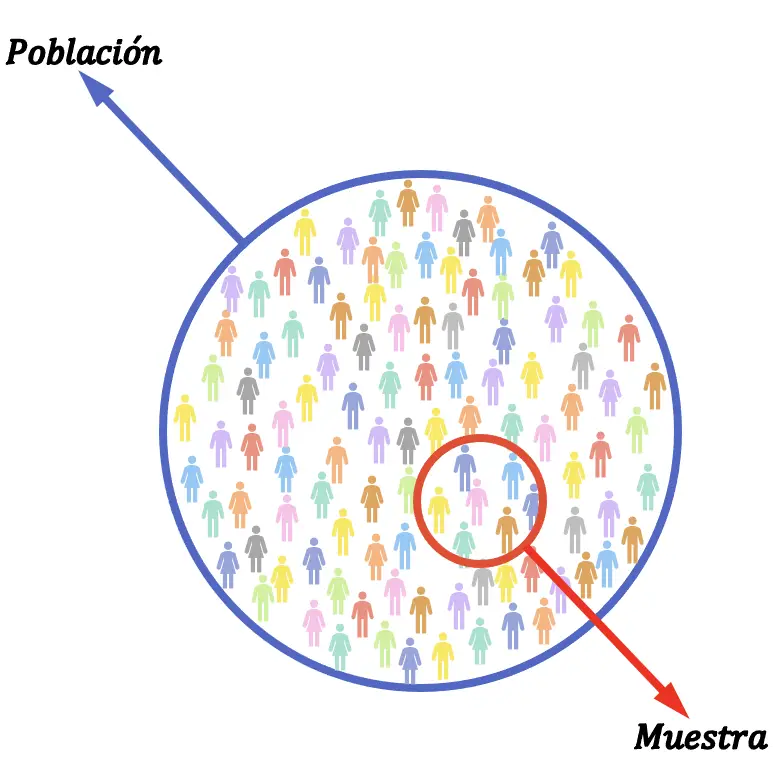
De statistische steekproef kan ook een subset van de populatie worden genoemd.
Om een populatie statistisch te bestuderen, worden normaal gesproken geen gegevens uit elk element van de populatie gehaald, maar wordt er een representatieve steekproef gekozen, wordt het onderzoek op de steekproef uitgevoerd en worden de bevindingen vervolgens geëxtrapoleerd naar de gehele populatie. bevolking.
Wanneer je bijvoorbeeld marktonderzoek wilt doen, bevraag je niet iedereen die geïnteresseerd is in jouw product, maar onderzoek je slechts een deel en met de verzamelde data bestudeer je de markt.
Opgemerkt moet worden dat de steekproefomvang (steekproefomvang) van een statistisch onderzoek niet triviaal is om te bepalen, want hoe groter de steekproefomvang, hoe beter deze de populatie vertegenwoordigt, maar hoe groter de steekproefomvang, hoe ingewikkelder de analyse. zal zijn. en daarom zullen er meer middelen en meer geld nodig zijn.