Stdev.p versus stdev.s in excel: wat is het verschil?

Er zijn drie verschillende functies die u kunt gebruiken om de standaardafwijking in Excel te berekenen:

1. STDEV.P: Deze functie berekent de standaarddeviatie van de populatie. Gebruik deze functie wanneer het waardenbereik de gehele populatie vertegenwoordigt.

Deze functie gebruikt de volgende formule:

Standaardafwijking populatie = √Σ (x _i – μ) ² / N

Goud:

• Σ: een Grieks symbool dat ‘som’ betekent
• x _i : de ^i- de waarde van de dataset
• μ: Het populatiegemiddelde
• N: Het totale aantal waarnemingen

2. STDEV.S: Deze functie berekent de standaardafwijking van het monster. Gebruik deze functie wanneer het waardenbereik een steekproef van waarden vertegenwoordigt in plaats van een hele populatie.

Deze functie gebruikt de volgende formule:

Standaardafwijking van de steekproef = √Σ (x _i – x ) ² / (n-1)

Goud:

• Σ: een Grieks symbool dat ‘som’ betekent
• x _i : de ^i- de waarde van de dataset
• x : De steekproefgemiddelden
• N: Het totale aantal waarnemingen

3. STDEV: Deze functie berekent ook de standaarddeviatie van de steekproef. Het retourneert exact dezelfde waarde als de STDEV.S -functie.

Technische notitie:

Omdat de formule voor de populatiestandaarddeviatie wordt gedeeld door N in plaats van n-1 , zal de standaarddeviatie van de populatie altijd kleiner zijn dan de standaarddeviatie van de steekproef.

De reden dat de standaarddeviatie van de populatie kleiner zal zijn, is omdat als we elke populatiewaarde kennen, we ook de exacte standaarddeviatie kennen.

Als we echter slechts een steekproef van de populatie hebben, hebben we meer onzekerheid over de exacte standaardafwijking van de totale populatie, dus onze schatting van de standaardafwijking moet groter zijn.

Het volgende voorbeeld laat zien hoe u deze functies in de praktijk kunt gebruiken.

Voorbeeld: STDEV.P versus STDEV.S in Excel

Stel dat we de volgende gegevensset in Excel hebben:

De volgende schermafbeelding laat zien hoe u de standaardafwijking van de gegevensset kunt berekenen met behulp van de drie verschillende standaardafwijkingsformules:

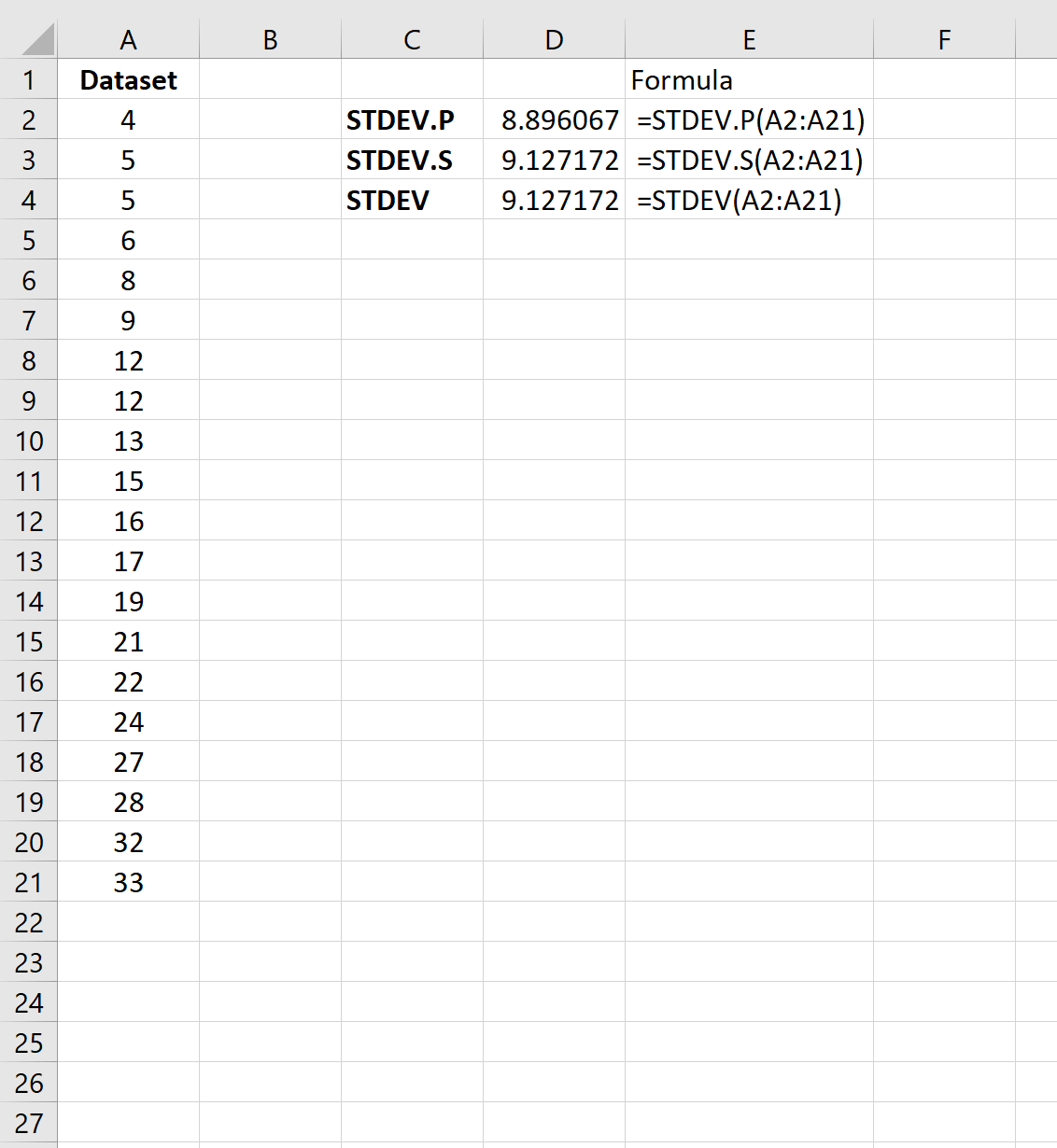
De standaarddeviatie van de steekproef blijkt 9,127 te zijn en de standaarddeviatie van de populatie blijkt 8,896 te zijn.

Zoals eerder vermeld zal de standaarddeviatie van de populatie altijd kleiner zijn dan de standaarddeviatie van de steekproef.

Wanneer STDEV.P versus STDEV.S gebruiken?

In de meeste gevallen zijn we niet in staat gegevens voor een hele populatie te verzamelen. We verzamelen daarom alleen gegevens voor een steekproef van de bevolking.

We gebruiken dus bijna altijd STDEV.S om de standaardafwijking van een dataset te berekenen, omdat onze dataset over het algemeen een steekproef vertegenwoordigt.

Houd er rekening mee dat STDEV en STDEV.S exact dezelfde waarden retourneren, dus we kunnen beide functies gebruiken om de standaardafwijking van het monster van een bepaalde gegevensset te berekenen.