Steekproefgrootte

Von Dr.benjamin anderson August 3, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat de steekproefomvang is en waarom dit belangrijk is in de statistiek. Daarnaast ontdek je hoe je de juiste steekproefomvang berekent en een opgeloste oefening zodat je kunt zien hoe je dat doet.

Wat is de steekproefomvang?

Steekproefgrootte (of steekproefomvang ) is het aantal personen waaruit de steekproef van een onderzoek bestaat. In de statistiek is de steekproefomvang belangrijk, zodat de steekproef representatief is voor de gehele populatie.

Daarom moet de steekproefomvang van een statistisch onderzoek groot genoeg zijn om de kenmerken van de gehele populatie te vertegenwoordigen. Aan de andere kant mag de steekproefomvang niet overdreven groot zijn, omdat het onderzoek dan duurder wordt. Concluderend moet de steekproefomvang voldoende zijn, niet te groot en niet te klein.

Als we bijvoorbeeld een analyse willen doen van de hoogte van een land, kunnen we niet vragen naar de lengte van alle inwoners van het land, omdat het onderzoek veel tijd zou kosten en te duur zou zijn. Het is daarom noodzakelijk om willekeurige steekproeven uit te voeren en alleen een representatieve steekproef van de bevolking te interviewen.

➤ Zie: Soorten bemonstering

En hoe kunnen we de juiste steekproefomvang kennen? In de volgende sectie zullen we zien hoe we de juiste steekproefomvang kunnen bepalen op basis van de onderzoeksvereisten.

Hoe de steekproefomvang te berekenen

Voor het schatten van een gemiddelde is de vereiste steekproefomvang gelijk aan het kwadraat van Z _α/2 vermenigvuldigd met de standaardafwijking (σ) gedeeld door de gewenste foutmarge (e). De formule voor het berekenen van de steekproefomvang is daarom:

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

Goud:

$n$

is de steekproefomvang.
$\alpha$

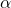
is het gewenste significantieniveau. Hierbij rekening houdend

$1-\alpha$

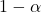
is het gewenste betrouwbaarheidsniveau.
$Z_{\alpha/2}$

is het kwantiel van de standaardnormale verdeling dat overeenkomt met een waarschijnlijkheid van α/2. Voor grote steekproeven en een betrouwbaarheidsniveau van 95% ligt dit gewoonlijk dicht bij 1,96 en voor een betrouwbaarheidsniveau van 99% ligt het gewoonlijk dicht bij 2,576.
$\sigma$

is de standaarddeviatie.

Houd er rekening mee dat in deze formule wordt aangenomen dat de populatieomvang oneindig is, dat wil zeggen dat de populatieomvang erg groot of onbekend is.

Opmerking: De bovenstaande formule is afgeleid van het betrouwbaarheidsformule-interval voor het gemiddelde .

Voorbeeld van berekening van de steekproefomvang

In dit gedeelte berekenen we als voorbeeld de juiste steekproefomvang voor een statistisch onderzoek.

We weten dat de standaarddeviatie van een populatie rond de 15 ligt, maar we kennen het gemiddelde niet, dus willen we een onderzoek uitvoeren om het gemiddelde te schatten. Welke steekproefomvang hebben we nodig als we een foutmarge van ±2 willen met een betrouwbaarheidsniveau van 95%?

Zoals we hierboven zagen, is de formule voor het berekenen van de steekproefomvang:

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

In dit geval is het gewenste betrouwbaarheidsniveau 95%, dus de overeenkomstige Z _α/2- waarde is 1,96.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

➤ Zie: Tabel met betrouwbaarheidsniveauwaarden

Nu we ten slotte weten hoeveel alle parameters waard zijn, vervangen we hun waarden in de formule en berekenen we de steekproefomvang:

$\begin{aligned}\displaystyle n&=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2\\[2ex] n&=\left(\frac{1,96\cdot 15}{2}\right)^2\\[2ex] n&=216,09 \approx 217 \end{array}$

Kortom, om het populatiegemiddelde met de gewenste vereisten te schatten, hebben we minimaal een steekproef van 217 individuen nodig.

Steekproefomvang, betrouwbaarheidsniveau en foutmarge

Afhankelijk van het betrouwbaarheidsniveau en de vereiste foutmarge zal de vereiste steekproefomvang variëren. De steekproefomvang, het betrouwbaarheidsniveau en de foutmarge zijn dus als volgt met elkaar verbonden:

De steekproefomvang en het betrouwbaarheidsniveau zijn direct proportioneel. Dat wil zeggen: als het betrouwbaarheidsniveau toeneemt, zal de steekproefomvang ook toenemen.
De steekproefomvang en de foutmarge zijn omgekeerd evenredig. Dus als de foutmarge groter wordt, zal de steekproefomvang afnemen.
Daarom kan het vergroten van de steekproefomvang het betrouwbaarheidsniveau vergroten of de foutmarge verkleinen.

Andere formules voor de steekproefomvang

Afhankelijk van de te schatten parameter varieert de formule voor de benodigde steekproefomvang enigszins. Daarom zullen we in deze sectie andere formules zien die nuttig kunnen zijn om de steekproefomvang in sommige speciale gevallen te berekenen.

steekproefomvang van een deel

De formule voor het berekenen van de steekproefomvang die nodig is om een aandeel (p) te schatten is:

$n=\cfrac{N\cdot Z_{\alpha/2}^2\cdot p\cdot (1-p)}{e^2\cdot (N-1)+Z_{\alpha/2}^2\cdot p\cdot (1-p)}$

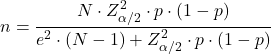
Steekproefomvang van een waarschijnlijkheid

Wanneer u een waarschijnlijkheid wilt schatten, wordt aanbevolen om de volgende formule te gebruiken om de benodigde steekproefomvang te bepalen:

$\displaystyle n=\left(\frac{Z_{\alpha/2}}{2\cdot e}\right)^2$

Steekproefgrootte voor het vergelijken van twee onafhankelijke gemiddelden

De formule voor het berekenen van de steekproefomvang bij het vergelijken van twee onafhankelijke gemiddelden met een bepaald α-risico en β-risico is als volgt:

$n=\cfrac{2\cdot \sigma^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

Goud

$\Delta$

is het verschil tussen de twee gemiddelden van de alternatieve hypothese.

Steekproefgrootte voor het vergelijken van twee gepaarde gemiddelden

Als je twee gepaarde gemiddelden met vaste fout α en fout β wilt vergelijken, is de formule die je moet gebruiken om het aantal waarnemingen in de steekproef te vinden:

$n=\cfrac{2\cdot \sigma_d^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

Goud

$\Delta$

is het verschil tussen de twee gepaarde gemiddelden van de alternatieve hypothese en

$\sigma_d^2$

Het is de variantie van de verschillen tussen twee metingen van hetzelfde individu.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder