Steekproefstandaardafwijking (of steekproefstandaardafwijking)

Von Dr.benjamin anderson August 3, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat de standaarddeviatie van een steekproef is in de statistiek. Op dezelfde manier leert u hoe u de standaarddeviatie van de steekproef kunt berekenen, een opgeloste oefening en wat het verschil is tussen de standaarddeviatie van de steekproef en de standaarddeviatie van de populatie. Ten slotte kunt u elke standaarddeviatie van een steekproef berekenen met een online rekenmachine.

Wat is de standaarddeviatie van de steekproef?

De standaardafwijking van het monster (of standaardafwijking van het monster ) is een spreidingsmaat die de variabiliteit van een monster aangeeft. Nauwkeuriger gezegd: de standaarddeviatie van de steekproef is gelijk aan de wortel van de som van de kwadraten van de afwijkingen gedeeld door de steekproefomvang min één.

Het symbool voor de standaarddeviatie van de steekproef is de kleine letter s .

De standaarddeviatie van de steekproef wordt soms de quasi-standaarddeviatie (of quasi-standaarddeviatie) genoemd om deze te onderscheiden van de standaarddeviatie van de populatie. Hieronder zullen we zien hoe de standaarddeviatie van de steekproef verschilt van de standaarddeviatie van de populatie.

Voorbeeld van standaardafwijkingsformule

De standaarddeviatie van de steekproef is gelijk aan de wortel van de som van de kwadraten van de afwijkingen van de steekproefgegevens gedeeld door de steekproefomvang min één. Daarom is de formule voor het berekenen van de standaarddeviatie van de steekproef :

formule voor de standaardafwijking van het monster of de standaardafwijking van het monster.png

Goud:

$s$

is de steekproefstandaardafwijking (of steekproefstandaardafwijking).
$x_i$

is de gegevenswaarde

$i$

.
$n$

is de steekproefomvang
$\overline{x}$

is het steekproefgemiddelde.

👉 U kunt de onderstaande rekenmachine gebruiken om de standaardafwijking van elk gegevensmonster te berekenen.

Voorbeeld van het berekenen van de standaardafwijking van het monster

Nu we de definitie van steekproefstandaarddeviatie (of steekproefstandaarddeviatie) kennen en wat de formule ervan is, zullen we een eenvoudig voorbeeld oplossen om te begrijpen hoe deze wordt berekend.

Een schoenenbedrijf voert marktonderzoek uit om te beslissen of er een nieuw schoenmodel op de markt komt. Omdat er veel verschillende modellen zijn en je gewoon een snelle voorlopige analyse wilt doen, besluit je om gewoon naar de prijs te kijken van een steekproef van de vijf beste concurrerende schoenenmerken (prijzen staan hieronder). Wat is de standaarddeviatie van deze dataset?

€ 98 € 70 € 125 € 89 € 75

Om de standaarddeviatie van de steekproef te berekenen, moeten we eerst het steekproefgemiddelde berekenen:

$\overline{x}=\cfrac{98+70+125+89+75}{5}=91,4$

Zodra het steekproefgemiddelde is berekend, passen we de formule voor de standaardafwijking van de steekproef toe:

$\displaystyle s=\sqrt{\frac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n-1}}$

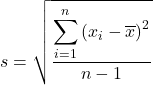
We vervangen de voorbeeldgegevens in de formule:

$\displaystyle s=\sqrt{\frac{\displaystyle (98-91,4)^2+(70-91,4)^2+(125-91,4)^2+(89-91,4)^2+(75-91,4)^2}{5-1}}$

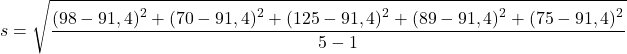
Het enige dat overblijft is dus het oplossen van de bewerkingen om de standaarddeviatie van de steekproef te berekenen:

$\begin{aligned}\displaystyle s&=\sqrt{\frac{6,6^2+(-21,4)^2+33,6^2+(-2,4)^2+(-16,4)^2}{4}}\\[2ex]\displaystyle s&=\sqrt{\frac{43,56+457,96+1128,96+5,76+268,96}{4}}\\[2ex]s&=\sqrt{\frac{1905,2}{4}}\\[2ex]s&=\sqrt{476,3}\\[2ex]s&=21,82 \end{aligned}$

Het steekproefverschil van het geanalyseerde monster bedraagt dus € 21,82.

➤ Zie: Bemonsteringsvariaties

Steekproefstandaardafwijking en populatiestandaardafwijking

Vervolgens gaan we kijken wat de verschillen zijn tussen de standaarddeviatie van de steekproef en de standaarddeviatie van de populatie, omdat dit twee verwante statistische concepten zijn waarover we duidelijk moeten zijn.

In estadística is de standaardafwijking van de populatie de standaardafwijking die wordt verkregen bij berekeningen met alle elementen van de populatie, hoewel de standaardafwijking de standaardafwijking is die wordt verkregen door de berekening uit te voeren met slechts één voorbeeld van gegevens uit de populatie .

Wiskundig gezien is het verschil tussen de standaarddeviatie van de steekproef en de standaarddeviatie van de populatie de noemer van de formule die voor de berekening ervan wordt gebruikt. Om de standaarddeviatie van de steekproef te berekenen, moet deze worden gedeeld door n-1, terwijl de standaarddeviatie van de populatie wordt berekend door te delen door n.

Om de standaarddeviatie van de steekproef te onderscheiden van de standaarddeviatie van de populatie, worden ze bovendien weergegeven door verschillende symbolen. Het symbool voor de standaarddeviatie van de steekproef is de letter s, terwijl het symbool voor de standaarddeviatie van de populatie de Griekse letter σ is.

Over het algemeen zijn niet alle elementen van een populatie bekend; het statistische onderzoek wordt daarom uitgevoerd op een steekproef van de populatie. De standaardafwijking van de steekproef wordt dus gebruikt om een puntschatting te maken van de waarde van de standaardafwijking van de gehele populatie.

➤ Zie: Standaarddeviatie van de populatie

Voorbeeld van standaarddeviatiecalculator

Voer de gegevens van een monster in de volgende online calculator in om de standaardafwijking van het monster (of de standaardafwijking van het monster) te berekenen. Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder