Wat is een steekproefverdeling?

Stel je voor dat er een populatie van 10.000 dolfijnen is en het gemiddelde gewicht van een dolfijn in die populatie is 300 pond.

Als we een eenvoudige willekeurige steekproef van 50 dolfijnen uit deze populatie nemen, kunnen we ontdekken dat het gemiddelde gewicht van de dolfijnen in deze steekproef 305 pond is.

Als we vervolgens nog een eenvoudig willekeurig monster van 50 dolfijnen nemen, kunnen we ontdekken dat het gemiddelde gewicht van de dolfijnen in dit monster 295 pond is.

Telkens wanneer we een eenvoudige willekeurige steekproef van 50 dolfijnen nemen, is het waarschijnlijk dat het gemiddelde gewicht van de dolfijnen in de steekproef dicht bij het populatiegemiddelde van 300 pond ligt, maar niet precies 300 pond.

Laten we ons voorstellen dat we 200 eenvoudige willekeurige monsters van 50 dolfijnen uit deze populatie nemen en een histogram maken van het gemiddelde gewicht van elk monster:

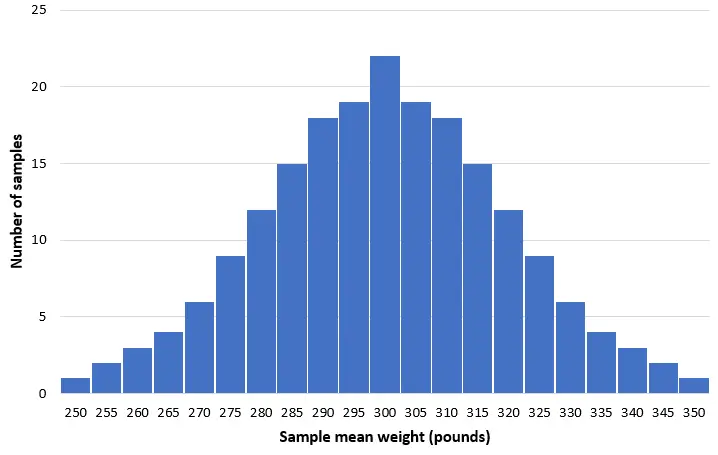
In de meeste monsters zal het gemiddelde gewicht bijna 300 pond bedragen. In zeldzame gevallen kunnen we een monster nemen vol kleine dolfijnen met een gemiddeld gewicht van slechts 250 pond. Of we nemen een monster vol tuimelaars van gemiddeld 350 pond. Over het algemeen zal de verdeling van de steekproefgemiddelden ongeveer normaal zijn, waarbij het centrum van de verdeling zich in het werkelijke centrum van de populatie bevindt.

Deze verdeling van steekproefgemiddelden staat bekend als de steekproefverdeling van het gemiddelde en heeft de volgende eigenschappen:

_µx = µ

waarbij μ _x het steekproefgemiddelde is en μ het populatiegemiddelde.

_σx = σ/√n

waarbij σ _x de standaarddeviatie van de steekproef is, σ de standaarddeviatie van de populatie is en n de steekproefomvang is.

In deze populatie dolfijnen weten we bijvoorbeeld dat het gemiddelde gewicht μ = 300 is. Het gemiddelde van de steekproefverdeling is dus μ _x = 300 .

Stel dat we ook weten dat de standaarddeviatie van de populatie 18 pond bedraagt. De standaarddeviatie van de steekproef is daarom σ _x = 18/ √50 = 2,546 .

Bemonsteringsverdeling van proporties

Neem dezelfde populatie van 10.000 dolfijnen. Stel dat 10% van de dolfijnen zwart is en de rest grijs. Stel dat we een eenvoudig willekeurig monster nemen van 50 dolfijnen en ontdekken dat 14% van de dolfijnen in dat monster zwart is. Vervolgens nemen we nog een eenvoudig willekeurig monster van 50 dolfijnen en ontdekken dat 8% van de dolfijnen in dit monster zwart is.

Stel je voor dat we 200 eenvoudige willekeurige monsters van 50 dolfijnen uit deze populatie nemen en een histogram maken van het aandeel zwarte dolfijnen in elk monster:

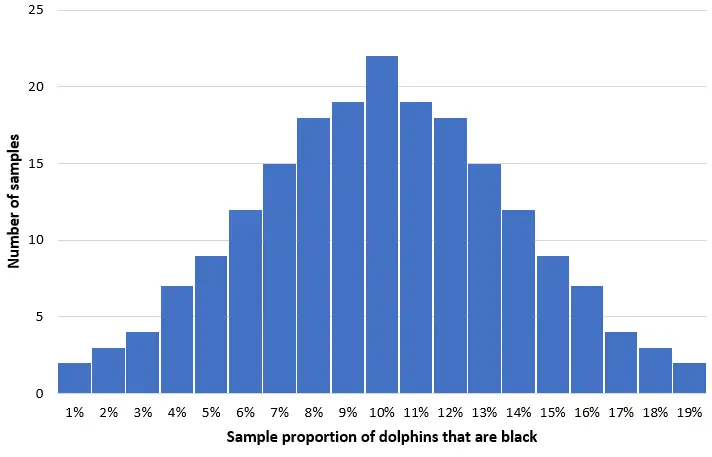
In de meeste monsters zal het aandeel zwarte dolfijnen dicht bij de werkelijke populatie van 10% liggen. De verdeling van het steekproefaandeel zwarte dolfijnen zal ongeveer normaal zijn, waarbij het centrum van de verdeling zich in het werkelijke centrum van de populatie bevindt.

Deze verdeling van de steekproefverhoudingen staat bekend als de steekproefverdeling van de verhoudingen en heeft de volgende eigenschappen:

_µp = P

waarbij p het steekproefaandeel is en P het populatieaandeel.

σ _p = √ (P)(1-P) / n

waarbij P het populatieaandeel is en n de steekproefomvang.

In deze dolfijnenpopulatie weten we bijvoorbeeld dat het werkelijke aandeel zwarte dolfijnen 10% = 0,1 is. Het gemiddelde van de proportiesteekproefverdeling is dus _μp = 0,1 .

Stel dat we ook weten dat de standaarddeviatie van de populatie 18 pond bedraagt. De standaarddeviatie van de steekproef is dus σ _p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042 .

Breng normaliteit tot stand

Om de bovenstaande formules te gebruiken, moet de steekproefverdeling normaal zijn.

Volgens de centrale limietstelling is de steekproefverdeling van een steekproefgemiddelde bij benadering normaal als de steekproefomvang groot genoeg is, zelfs als de populatieverdeling niet normaal is . In de meeste gevallen beschouwen wij een steekproefomvang van 30 of meer als groot genoeg.

De steekproefverdeling van een steekproefaandeel is bij benadering normaal als het verwachte aantal successen en mislukkingen beide minstens 10 bedraagt.

Voorbeelden

We kunnen steekproefverdelingen gebruiken om kansen te berekenen.

Voorbeeld 1: Een bepaalde machine maakt cookies aan. De gewichtsverdeling van deze koekjes is scheef naar rechts met een gemiddelde van 10 ounces en een standaarddeviatie van 2 ounces. Als we een eenvoudige willekeurige steekproef nemen van 100 door deze machine geproduceerde koekjes, wat is dan de kans dat het gemiddelde gewicht van de koekjes in deze steekproef minder dan 9,8 gram bedraagt?

Stap 1: Breng normaliteit tot stand.

We moeten ervoor zorgen dat de steekproefverdeling van de steekproefgemiddelden normaal is. Omdat onze steekproefomvang groter is dan of gelijk is aan 30, kunnen we volgens de centrale limietstelling aannemen dat de steekproefverdeling van de steekproefgemiddelden normaal is.

Stap 2: Zoek het gemiddelde en de standaardafwijking van de steekproefverdeling.

_µx = µ

_σx = σ/√n

_μx = 10 ounces

σ _x = 2/ √100 = 2/10 = 0,2 ounce

Stap 3: Gebruik de Z-Score Area Calculator om de waarschijnlijkheid te bepalen dat het gemiddelde koekjesgewicht in dit voorbeeld minder dan 9,8 ounces is.

Voer de volgende getallen in de Z-scoregebiedcalculator in. U kunt „Ruwe score 2“ blanco laten, aangezien we in dit voorbeeld slechts één getal vinden.

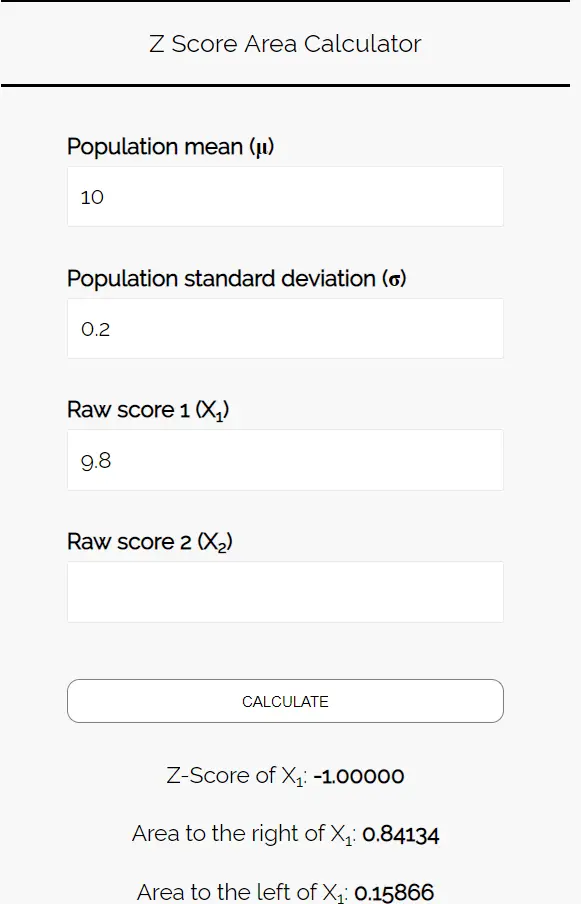
Omdat we de waarschijnlijkheid willen weten dat het gemiddelde gewicht van de koekjes in dit monster minder dan 9,8 gram bedraagt, zijn we geïnteresseerd in het gebied links van 9,8. De rekenmachine vertelt ons dat deze kans 0,15866 is.

Voorbeeld 2: Volgens een schoolbreed onderzoek geeft 87% van de leerlingen op een bepaalde school de voorkeur aan pizza boven ijs. Stel dat we een eenvoudige willekeurige steekproef van 200 studenten nemen. Hoe groot is de kans dat het percentage studenten dat de voorkeur geeft aan pizza minder dan 85% bedraagt?

Stap 1: Breng normaliteit tot stand.

Bedenk dat de steekproefverdeling van een steekproefaandeel ongeveer normaal is als het verwachte aantal ‘successen’ en ‘mislukkingen’ beide minstens 10 zijn.

In dit geval is het verwachte aantal studenten dat de voorkeur geeft aan pizza 87% * 200 studenten = 174 studenten. Het verwachte aantal studenten dat geen voorkeur heeft voor pizza is 13% * 200 studenten = 26 studenten. Aangezien beide getallen minstens 10 zijn, kunnen we aannemen dat de steekproefverdeling van het aandeel studenten dat de voorkeur geeft aan pizza ongeveer normaal is.

Stap 2: Zoek het gemiddelde en de standaardafwijking van de steekproefverdeling.

_µp = P

σ _p = √ (P)(1-P) / n

_µp = 0,87

σ _p = √ (0,87)(1-0,87) / 200 = 0,024

Stap 3: Gebruik de Z-Score Area Calculator om de waarschijnlijkheid te bepalen dat het percentage studenten dat de voorkeur geeft aan pizza minder dan 85% is.

Voer de volgende getallen in de Z-scoregebiedcalculator in. U kunt „Ruwe score 2“ blanco laten, aangezien we in dit voorbeeld slechts één getal vinden.

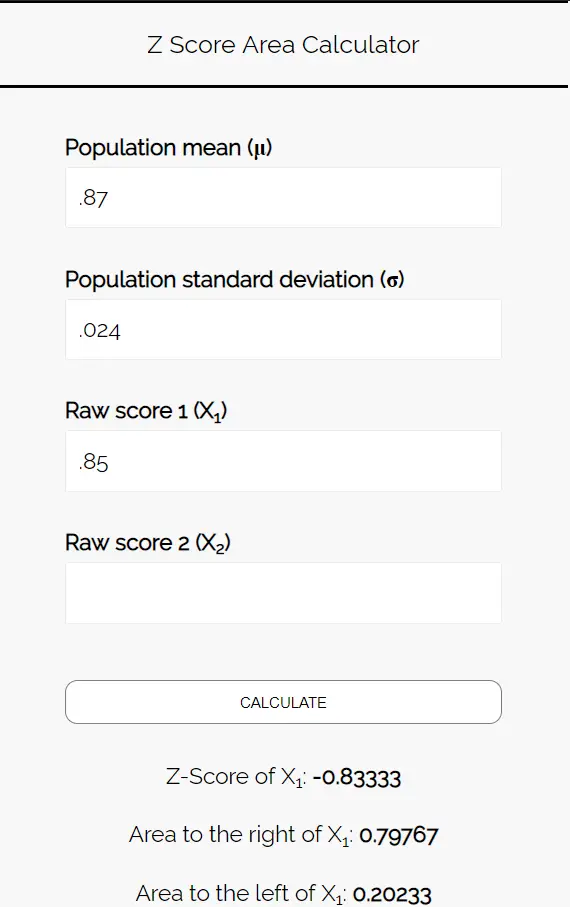
Omdat we willen weten hoe waarschijnlijk het is dat het percentage studenten dat de voorkeur geeft aan pizza kleiner is dan 85%, zijn we geïnteresseerd in het gebied links van 0,85. De rekenmachine vertelt ons dat deze kans 0,20233 is.