Hoe bemonsteringsverdelingen in excel te berekenen

Een steekproefverdeling is een waarschijnlijkheidsverdeling van een bepaalde statistiek gebaseerd op veel willekeurige steekproeven uit een enkele populatie .

In deze zelfstudie wordt uitgelegd hoe u het volgende kunt doen met steekproefverdelingen in Excel:

• Genereer een steekproefverdeling.
• Visualiseer de steekproefverdeling.
• Bereken het gemiddelde en de standaardafwijking van de steekproefverdeling.
• Bereken de kansen met betrekking tot de steekproefverdeling.

Genereer een steekproefverdeling in Excel

Stel dat we een steekproefverdeling willen genereren die bestaat uit 1.000 steekproeven, waarbij elke steekproefomvang 20 is en voortkomt uit een normale verdeling met een gemiddelde van 5,3 en een standaarddeviatie van 9 .

We kunnen dit eenvoudig doen door de volgende formule in cel A2 van onze spreadsheet te typen:

 = NORM . INV ( RAND (), 5.3, 9)

We kunnen dan over de rechteronderhoek van de cel bewegen totdat een kleine + verschijnt en de formule 20 cellen naar rechts en 1000 cellen naar beneden slepen:

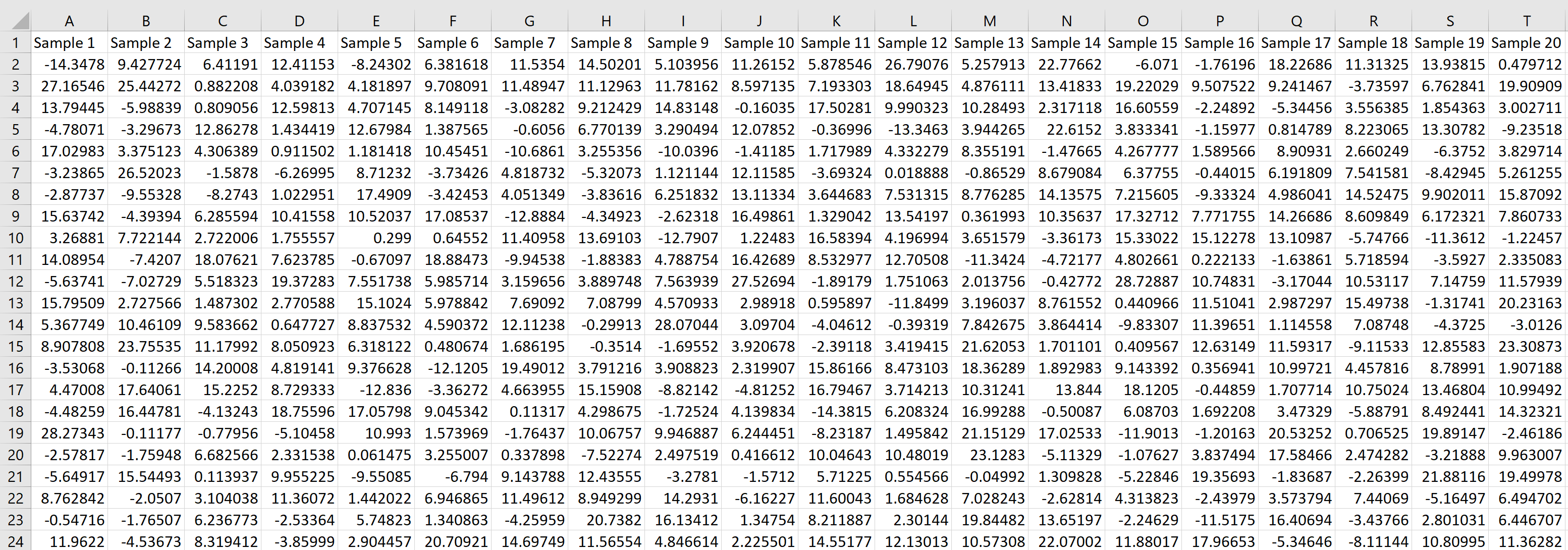
Elke rij vertegenwoordigt een steekproef van grootte 20, waarbij elke waarde afkomstig is uit een normale verdeling met een gemiddelde van 5,3 en een standaarddeviatie van 9.

Zoek het gemiddelde en de standaarddeviatie

Om het gemiddelde en de standaardafwijking van deze steekproefverdeling van steekproefgemiddelden te vinden, kunnen we eerst het gemiddelde van elk monster vinden door de volgende formule in cel U2 van ons werkblad te typen:

 = AVERAGE (A2:T2)

We kunnen dan over de rechteronderhoek van de cel bewegen totdat een kleine + verschijnt en dubbelklikken om deze formule naar alle andere cellen in kolom U te kopiëren:

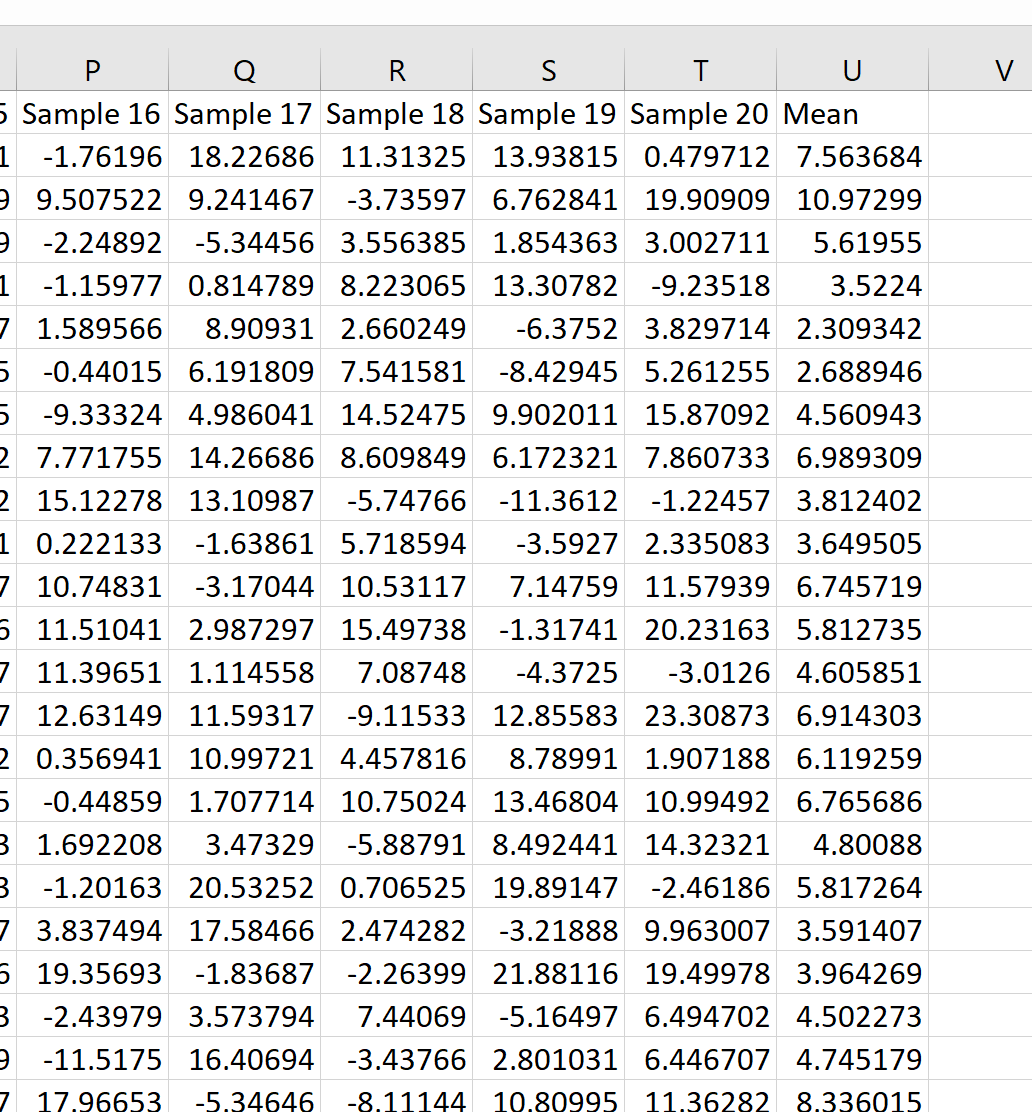
We kunnen zien dat het eerste monster een gemiddelde van 7,563684 had, het tweede monster een gemiddelde van 10,97299, enzovoort.

We kunnen dan de volgende formules gebruiken om het gemiddelde en de standaardafwijking van de steekproefgemiddelden te berekenen:

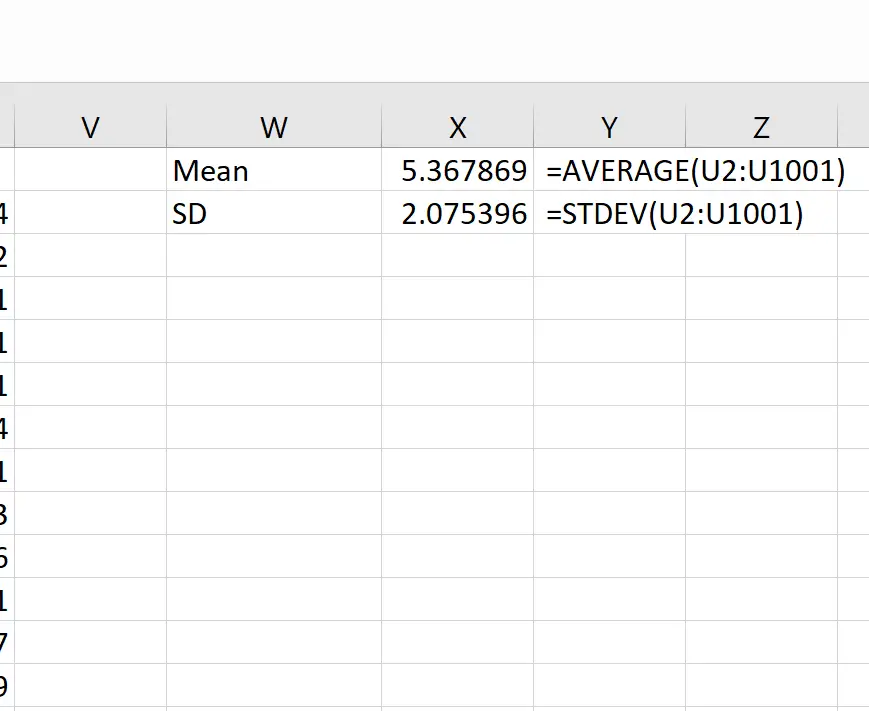
Theoretisch zou het gemiddelde van de steekproefverdeling 5,3 moeten zijn. We kunnen zien dat het werkelijke steekproefgemiddelde in dit voorbeeld 5.367869 is, wat dicht bij 5.3 ligt.

En theoretisch zou de standaardafwijking van de steekproefverdeling gelijk moeten zijn aan s/√n, wat 9 / √20 = 2,012 zou zijn. We kunnen zien dat de werkelijke standaardafwijking van de steekproefverdeling 2,075396 is, wat dichtbij 2,012 ligt.

Visualiseer de steekproefverdeling

We kunnen ook een eenvoudig histogram maken om de steekproefverdeling van steekproefgemiddelden te visualiseren.

Om dit te doen, markeert u eenvoudigweg alle steekproefgemiddelden in kolom U, klikt u op het tabblad Invoegen en klikt u vervolgens op de optie Histogram onder het gedeelte Grafieken .

Dit geeft het volgende histogram:

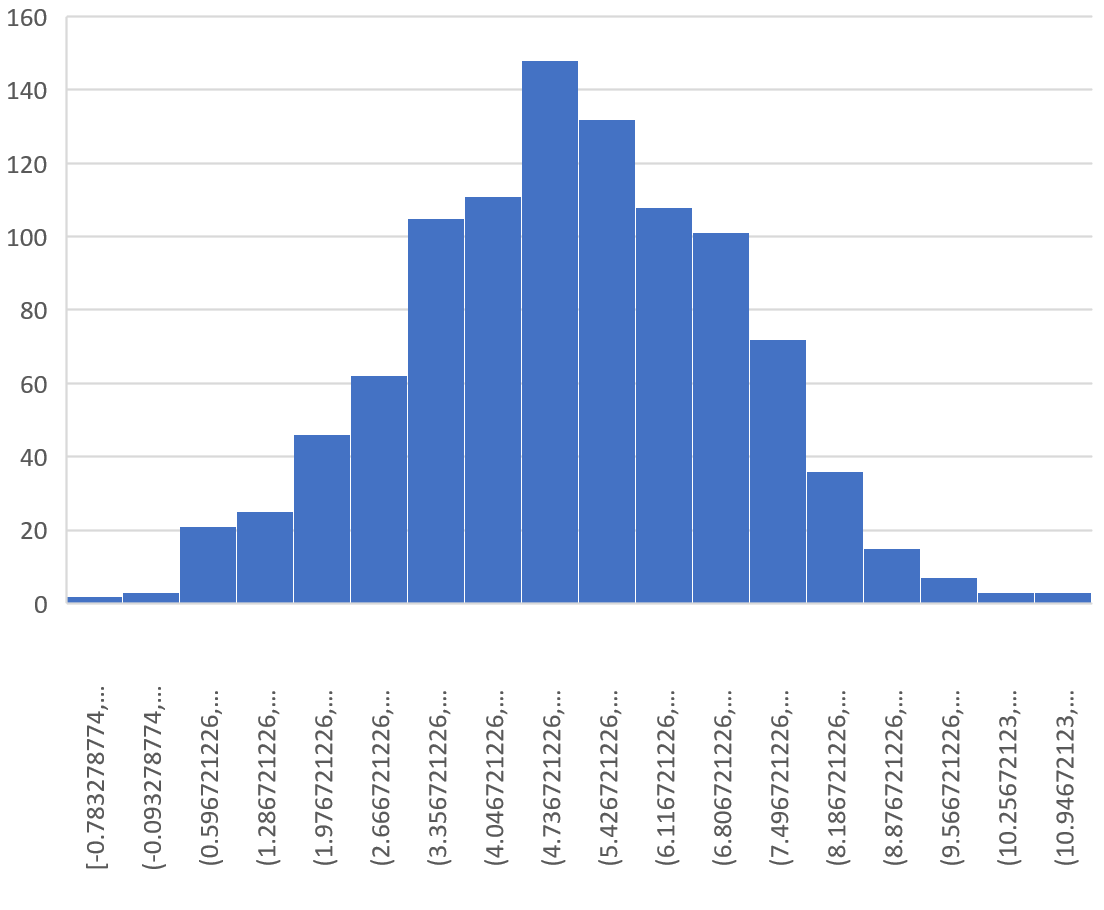
Het is te zien dat de steekproefverdeling klokvormig is met een piek nabij de waarde 5.

Aan de staarten van de verdeling kunnen we echter zien dat sommige steekproeven gemiddelden groter dan 10 hadden en andere gemiddelden kleiner dan 0.

Bereken de kansen

We kunnen ook de waarschijnlijkheid berekenen dat een bepaalde waarde voor een steekproefgemiddelde wordt verkregen, op basis van het populatiegemiddelde, de populatiestandaarddeviatie en de steekproefomvang.

We kunnen bijvoorbeeld de volgende formule gebruiken om de waarschijnlijkheid te vinden dat het steekproefgemiddelde kleiner is dan of gelijk is aan 6, gegeven dat het populatiegemiddelde 5,3 is, de standaarddeviatie van de populatie 9 is en de steekproefomvang:

 = COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)

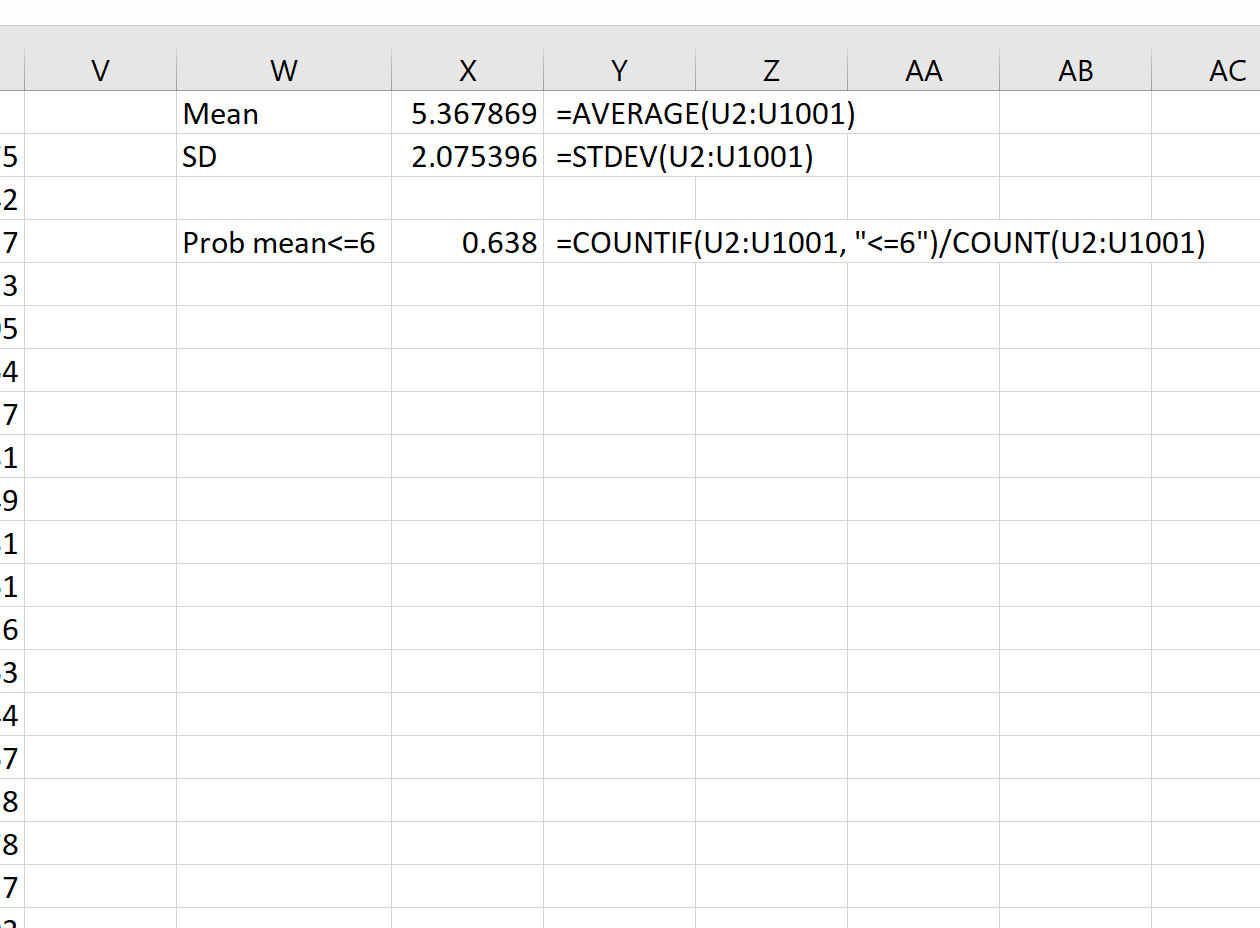
We zien dat de kans dat het steekproefgemiddelde kleiner is dan of gelijk is aan 6 0,638 is.

Dit komt zeer dicht in de buurt van de waarschijnlijkheid berekend door de Sampling Distribution Calculator :

Aanvullende bronnen

Een inleiding tot bemonsteringsverdelingen
Bemonsteringsdistributiecalculator
Een inleiding tot de centrale limietstelling