Steekproefverdeling van verschil in gemiddelden

Von Dr.benjamin anderson August 3, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat de steekproefverdeling van het verschil tussen twee gemiddelden in de statistiek is. Ook vindt u hier de formule voor de steekproevenverdeling van het verschil in gemiddelden en daarnaast een stapsgewijs op te lossen oefening.

Wat is de steekproefverdeling van het verschil in gemiddelden?

De steekproefverdeling van het verschil in gemiddelden is de verdeling die het resultaat is van het berekenen van de verschillen tussen de gemiddelden van alle mogelijke steekproeven uit twee verschillende populaties.

Dat wil zeggen dat om de steekproefverdeling van het verschil in gemiddelden te verkrijgen, alle mogelijke steekproeven uit twee onderzoekspopulaties moeten worden geselecteerd, vervolgens wordt het gemiddelde van elke geselecteerde steekproef berekend en ten slotte het verschil tussen alle gemiddelden berekend uit de twee populaties. De reeks waarden die wordt verkregen na toepassing van al deze bewerkingen vormt dus de steekproefverdeling van het verschil in gemiddelden.

steekproefverdeling van verschil in gemiddelden

De verschil-in-gemiddelde-steekproefverdeling wordt gebruikt om de waarschijnlijkheid te berekenen dat het verschil tussen twee gemiddelden van willekeurig geselecteerde steekproeven uit twee verschillende populaties dicht bij het verschil in de populatiegemiddelden ligt.

➤ Zie: Steekproefverdeling van het gemiddelde

Formule voor de steekproefverdeling van verschil in gemiddelden

Als de steekproefomvang groot genoeg is (n ₁ ≥30 en n ₂ ≥30), volgt de steekproefverdeling van het verschil in gemiddelden een normale verdeling. Meer precies worden de parameters van genoemde verdeling als volgt berekend:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

Opmerking: Als beide populaties normale verdelingen zijn, volgt de steekproefverdeling van het verschil in gemiddelden een normale verdeling, ongeacht de steekproefomvang.

Omdat de steekproefverdeling van het verschil in gemiddelden wordt gedefinieerd door een normale verdeling, is de formule voor het berekenen van de statistiek van de steekproefverdeling van het verschil in gemiddelden daarom:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Goud:

$\overline{x_i}$

is het gemiddelde van monster i.
$\mu_i$

is het gemiddelde van de populatie i.
$\sigma_i$

is de standaardafwijking van populatie i.
$n_i$

is de steekproefomvang i.
$Z$

is een variabele gedefinieerd door de standaard normale verdeling N(0,1).

Houd er rekening mee dat steekproeven uit verschillende populaties verschillende steekproefgroottes kunnen hebben.

Concreet voorbeeld van de steekproefverdeling van het verschil in gemiddelden

Zodra we de definitie van het verschil in de steekproevenverdeling zien en wat de formule ervan is, zullen we een stapsgewijs voorbeeld zien om het begrip van het verschil in de steekproevenverdeling te voltooien.

In een statistisch onderzoek willen we het verschil analyseren tussen de lengte van jongens en meisjes van een bepaalde leeftijd. We weten dat de verdeling die de populatie jongens van deze leeftijd definieert een gemiddelde heeft van 157 cm en een standaarddeviatie van 9 cm, en aan de andere kant heeft de verdeling die de populatie meisjes van deze leeftijd definieert een gemiddelde van 148 cm. cm en een standaardafwijking van 7 cm. Als er een steekproef van 30 jongens van deze leeftijd en een steekproef van 35 meisjes van deze leeftijd wordt getrokken, wat is dan de kans dat de gemiddelde lengte van de steekproef jongens 12 cm groter is dan de gemiddelde lengte van de steekproef meisjes?

Om dit probleem op te lossen, is het eerste wat u moet doen het berekenen van de statistiek van het verschil in de steekproefverdeling. We passen daarom de bovenstaande formule toe:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right)}=\cfrac{12-(157-148)}{\displaystyle\sqrt{\frac{9^2}{30}+\frac{7^2}{35}}}=1,48$

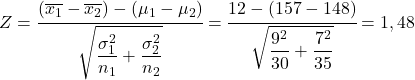
Daarom is de kans dat de gemiddelde steekproeflengte van jongens 12 cm groter is dan de gemiddelde lengte van meisjes gelijk aan de kans dat de Z-variabele groter is dan 1,48.

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]“ title=“Rendered by QuickLaTeX.com“ height=“19″ width=“253″ style=“vertical-align: -5px;“></p> </p> <p> We zoeken daarom naar de waarschijnlijkheid van Z>1,48 in de <a href=$ tabel van Z :

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694″ title=“Rendered by QuickLaTeX.com“ height=“19″ width=“331″ style=“vertical-align: -5px;“></p> </p> <p> Kortom, de kans dat de gemiddelde steekproeflengte van jongens 12 cm groter is dan de gemiddelde lengte van meisjes is 6,94%.</p> </div>  <div class=$

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder

Wat is de steekproefverdeling van het verschil in gemiddelden?

Formule voor de steekproefverdeling van verschil in gemiddelden

Concreet voorbeeld van de steekproefverdeling van het verschil in gemiddelden

Über den Autor

Dr.benjamin anderson

Einen Kommentar hinzufügen