Bemonsteringsverdeling van verschil in verhoudingen

In dit artikel wordt uitgelegd wat het verschil in de proportionele steekproefverdeling is en waarvoor dit in de statistieken wordt gebruikt. Ook worden de formule voor de verdeling van het verschil in proporties en een stapsgewijze opgeloste oefening gepresenteerd.

Wat is de steekproefverdeling van het verschil in verhoudingen?

Het verschil in de steekproefverdeling is de verdeling die het resultaat is van het berekenen van de verschillen tussen de steekproefverhoudingen van alle mogelijke steekproeven uit twee verschillende populaties.

Dat wil zeggen dat het proces voor het verkrijgen van de steekproefverdeling van het verschil in verhoudingen in de eerste plaats bestaat uit het extraheren van alle mogelijke steekproeven uit twee verschillende populaties, in de tweede plaats het bepalen van de proportie van elk geëxtraheerd monster, en ten slotte het bepalen van het verschil tussen alle proporties van het verschil in proporties. twee populaties. Zodat de reeks resultaten verkregen na het uitvoeren van deze bewerkingen de steekproefverdeling van het verschil in verhoudingen vormt.

In de statistiek wordt het verschil in de steekproefverdeling gebruikt om de waarschijnlijkheid te berekenen dat het verschil tussen de steekproefaandelen van twee willekeurig geselecteerde steekproeven dicht bij het verschil in de populatieaandelen ligt.

Formule voor de bemonsteringsverdeling van het verschil in verhoudingen

De steekproeven die zijn geselecteerd op basis van het verschil in de steekproevenverdeling worden gedefinieerd door binomiale verdelingen , omdat voor praktische doeleinden een aandeel de verhouding is tussen succesvolle gevallen en het totale aantal waarnemingen.

Niettemin kunnen binomiale verdelingen, vanwege de centrale limietstelling, worden benaderd als normale waarschijnlijkheidsverdelingen . Daarom kan de steekproefverdeling van het verschil in verhoudingen worden benaderd tot een normale verdeling met de volgende kenmerken:

Opmerking: De steekproefverdeling van het verschil in verhoudingen kan alleen worden benaderd als een normale verdeling als:

,

,

,

,

En

.

Omdat de steekproefverdeling van het verschil in verhoudingen kan worden benaderd tot een normale verdeling, is de formule voor het berekenen van de statistiek van de steekproefverdeling van het verschil in verhoudingen daarom als volgt:

Goud:

• 

  is de steekproefaandeel i.

• 

  is het aandeel van de bevolking i.

• 

  is de kans op falen van populatie i,

  

  .

• 

  is de steekproefomvang i.

• 

  is een variabele gedefinieerd door de standaard normale verdeling N(0,1).

Deze formule is vergelijkbaar met de formule voor het testen van hypothesen voor verschillen in verhoudingen.

Concreet voorbeeld van de steekproefverdeling van het verschil in verhoudingen

Nadat u de definitie van de bemonsteringsverdeling van het verschil in verhoudingen hebt gezien en wat de formule ervan is, kunt u hieronder stap voor stap een opgelost voorbeeld zien om het concept beter te begrijpen.

• Je wilt de nauwkeurigheid van twee productie-installaties analyseren: de ene fabriek produceert op zo’n manier dat slechts 5% van de geproduceerde onderdelen gebreken vertoont, terwijl het percentage defecte onderdelen in een andere fabriek 8% bedraagt. Als we een monster nemen van 200 onderdelen uit de eerste fabriek en nog een monster van 280 onderdelen uit de tweede fabriek, wat is dan de kans dat het percentage defecten in de eerste productie-installatie groter is dan het percentage defecten in de tweede fabriek? productie?

Om alle gegevens van het probleem te kennen, zullen we eerst het aandeel goed geproduceerde delen van elke plant berekenen:

Als het defectpercentage in de eerste fabriek groter was dan het defectpercentage in de tweede fabriek, betekent dit dat de volgende vergelijking waar zou zijn:

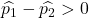
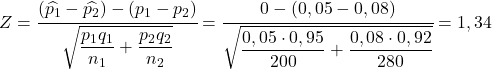
De kans dat het defectpercentage van de eerste fabriek groter is dan het defectpercentage van de tweede fabriek is dus gelijk aan de waarschijnlijkheid dat de variabele Z groter is dan 1,34:

normale verdelingstabel te zoeken en hebben we het probleem al opgelost:

➤ Zie: Steekproefverdeling van verschil in gemiddelden