Hoe u een stam- en bladplot met decimalen maakt

Een stam- en bladdiagram is een type diagram dat gegevens weergeeft door elke waarde in een gegevensset te verdelen in een ’stam‘ en een ‚blad‘.

Stel dat we bijvoorbeeld de volgende gegevensset hebben:

Gegevensset: 12, 14, 18, 22, 22, 23, 25, 25, 28, 45, 47, 48

Als we het eerste cijfer van elke waarde definiëren als de „stengel“ en het tweede cijfer als het „blad“, kunnen we het volgende stam- en bladdiagram maken:

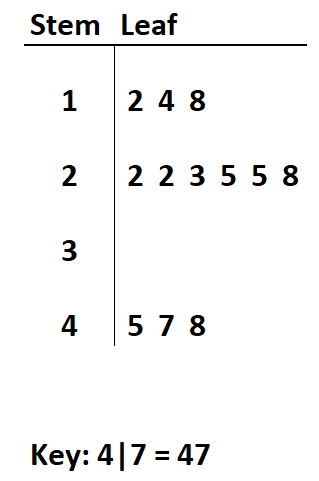
Hoewel stam- en bladplots doorgaans worden gebruikt met gehele waarden, kunnen ze ook worden gebruikt voor waarden met decimalen.

De volgende voorbeelden illustreren hoe u stengel- en bladplots met decimalen kunt maken.

Voorbeeld 1: Stam- en bladgrafiek met één decimaal

Stel dat we de volgende dataset hebben:

Gegevensset: 11.6, 12.2, 12.5, 12.6, 13.7, 13.8, 14.1, 15.2

Als we de getallen vóór de komma definiëren als stengel en de getallen na de komma als blad, kunnen we het volgende stengel- en bladdiagram maken:

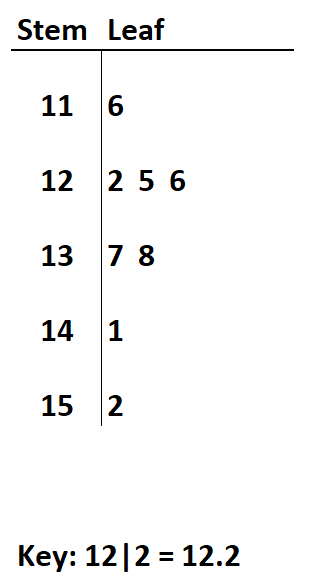
Bij het maken van dit stengel- en bladdiagram is het belangrijk om onderaan een sleutel op te nemen, zodat de lezer weet hoe hij de stengel- en bladwaarden moet interpreteren.

Voorbeeld 2: Stam- en bladgrafiek met meerdere decimalen

Stel dat we de volgende dataset hebben:

Gegevensset: 3.26, 3.28, 3.34, 3.38, 3.41, 3.42, 3.44, 3.59, 3.63

Als we het gehele getal en de eerste waarde na de komma instellen als de stam, en de tweede waarde na de decimaal als het blad, dan kunnen we de volgende stam- en bladplot maken:

Nogmaals, de sleutel onderaan de plot vertelt ons hoe we de plotwaarden moeten interpreteren.

Voorbeeld 3: Een stam- en bladdiagram interpreteren met decimalen

Stel dat we het volgende stam- en bladdiagram met decimalen hebben:

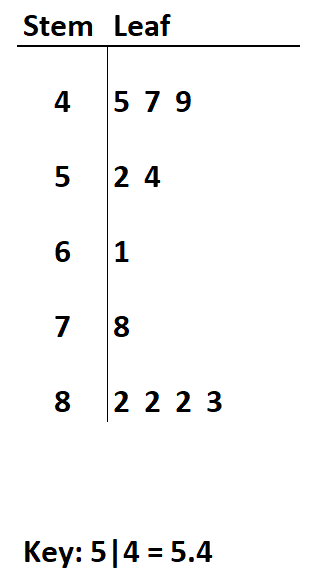
Vraag 1: Wat is de maximale waarde in de dataset?

De maximale waarde zou 8,3 zijn.

Vraag 2: Wat is de reikwijdte van de dataset?

Het bereik van de dataset is het verschil tussen de grootste en de kleinste waarde. Het bereik zou dus 8,3 – 4,5 = 3,8 zijn.

Vraag 3: Wat is de modus van de dataset?

De modus is de waarde die het vaakst voorkomt. Dat zou 8,2 zijn.

Vraag 4: Wat is de mediaan van de dataset?

De mediaan wordt gedefinieerd als de “gemiddelde” waarde van de dataset. Om deze waarde te vinden, kunnen we elk van de individuele waarden in de dataset schrijven en de mediaanwaarde vinden:

Gegevensset: 4.5, 4.7, 4.9, 5.2, 5.4, 6.1 , 7.8, 8.2, 8.2, 8.2, 8.3

De mediaan bedraagt 6,1 .

Aanvullende bronnen

Een inleiding tot stam- en bladplots
Een inleiding tot back-to-back stengel- en bladplots
Stam- en bladplotgenerator
Hoe u een stam- en bladplot maakt in Excel