De regel van sturges

In dit artikel wordt uitgelegd wat de regel van Sturges is en wat de formule ervan is. Ook vindt u een stapsgewijs concreet voorbeeld van de regel van Sturges en daarnaast een online regelcalculator van Sturges.

Wat is de regel van Sturges?

De regel van Sturges is een regel die wordt gebruikt om het ideale aantal klassen of intervallen te berekenen waarin een dataset moet worden verdeeld.

De formule voor de regel van Sturges stelt dat het aantal klassen gelijk is aan één plus de logaritme met grondtal twee van het totale aantal gegevens.

Goud

is het aantal klassen of intervallen en

is het totale aantal waarnemingen in de steekproef.

De Sturges-regel werd in 1926 gecreëerd door de Duitse statisticus Herbert Sturges.

Voorbeeld van de Sturges-regel

Nu we weten wat de regel van Sturges is, zullen we door een stapsgewijze oefening op te lossen zien hoe de intervallen van een dataset worden berekend met behulp van de regel van Sturges in de statistiek.

• De steekproefomvang van 50 verschillende mensen werd gemeten en alle waarden werden vastgelegd in de volgende gegevenstabel. Pas de regel van Sturges toe om de gegevensset in intervallen te verdelen en zet de gegevens vervolgens in een histogram.

Eerst moeten we de gegevens in intervallen verdelen. In totaal zijn er 50 gegevenselementen, dus we gebruiken de regel van Sturges met deze waarde:

Het is daarom noodzakelijk om de gegevens te scheiden en in zeven intervallen te groeperen. We moeten nu de breedte van elk interval weten. Om dit te doen, deelt u eenvoudigweg de maximale waarde minus de minimumwaarde door het totale aantal intervallen:

Kortom, er moeten 7 intervallen zijn met een amplitude van 9, dus de intervallen berekend met de Sturges-methode zijn:

Nadat we de intervallen hebben berekend, moeten we het aantal keren tellen dat een stukje gegevens in elk interval voorkomt en de frequentietabel samenstellen:

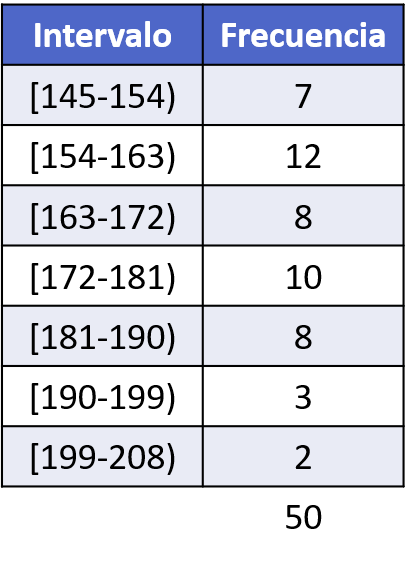
Ten slotte kunnen we vanuit de frequentietabel het histogram maken om de gegevens in een grafiek weer te geven:

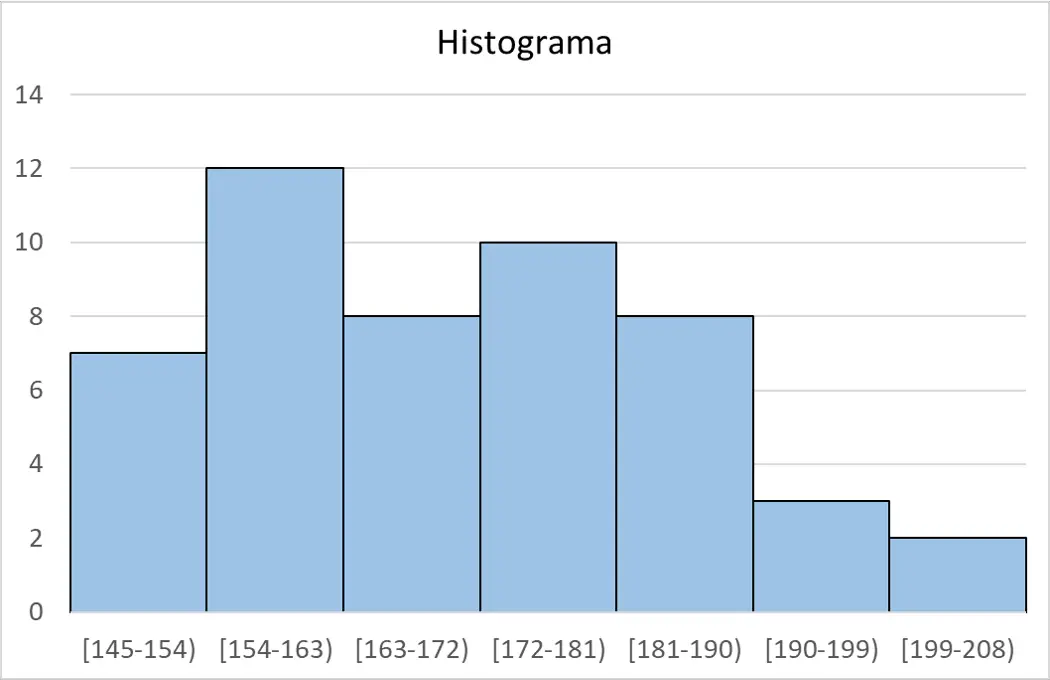
Sturges-regelcalculator

Voer het totale aantal gegevensmonsters in en klik op „Berekenen“, waarna de rekenmachine het aantal intervallen retourneert dat is berekend volgens de regel van Sturges.