Hoe u een correlatie-t-test uitvoert

Een Pearson-correlatiecoëfficiënt wordt gebruikt om de lineaire associatie tussen twee variabelen te kwantificeren.

Er is altijd een waarde tussen -1 en 1 nodig, waarbij:

• -1 duidt op een volkomen negatieve lineaire correlatie.
• 0 geeft aan dat er geen lineaire correlatie is.
• 1 geeft een perfect positieve lineaire correlatie aan.

Om te bepalen of een correlatiecoëfficiënt statistisch significant is, kunt u een t-test uitvoeren, waarbij een t-score en een bijbehorende p-waarde worden berekend.

De formule om de t-score te berekenen is als volgt:

t = r√ (n-2) / (1-r ² )

Goud:

• r: De correlatiecoëfficiënt
• n: De steekproefomvang

De p-waarde wordt berekend als de overeenkomstige tweezijdige p-waarde voor de t-verdeling met n-2 vrijheidsgraden.

In het volgende voorbeeld ziet u hoe u een t-test uitvoert voor een correlatiecoëfficiënt.

Voorbeeld: uitvoeren van een t-test voor correlatie

Stel dat we de volgende gegevensset hebben met twee variabelen:

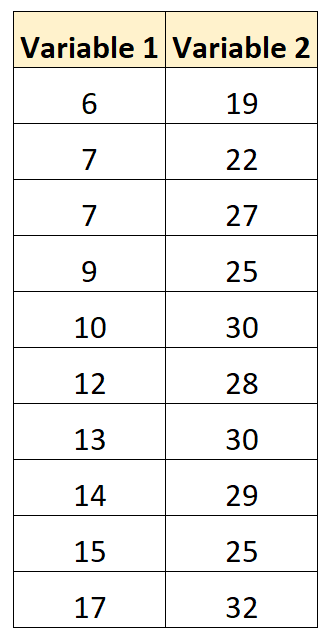
Met behulp van bepaalde statistische software (Excel, R, Python, enz.) kunnen we de correlatiecoëfficiënt tussen de twee variabelen berekenen op 0,707 .

Dit is een zeer positieve correlatie, maar om te bepalen of deze statistisch significant is, moeten we de bijbehorende t-score en p-waarde berekenen.

We kunnen de t-score als volgt berekenen:

• t = r√ (n-2) / (1-r ² )
• t = 0,707√ (10-2) / (1-0,707 ² )
• t = 2,828

Met behulp van een P-waarde T-score-calculator vinden we dat de overeenkomstige p-waarde 0,022 is.

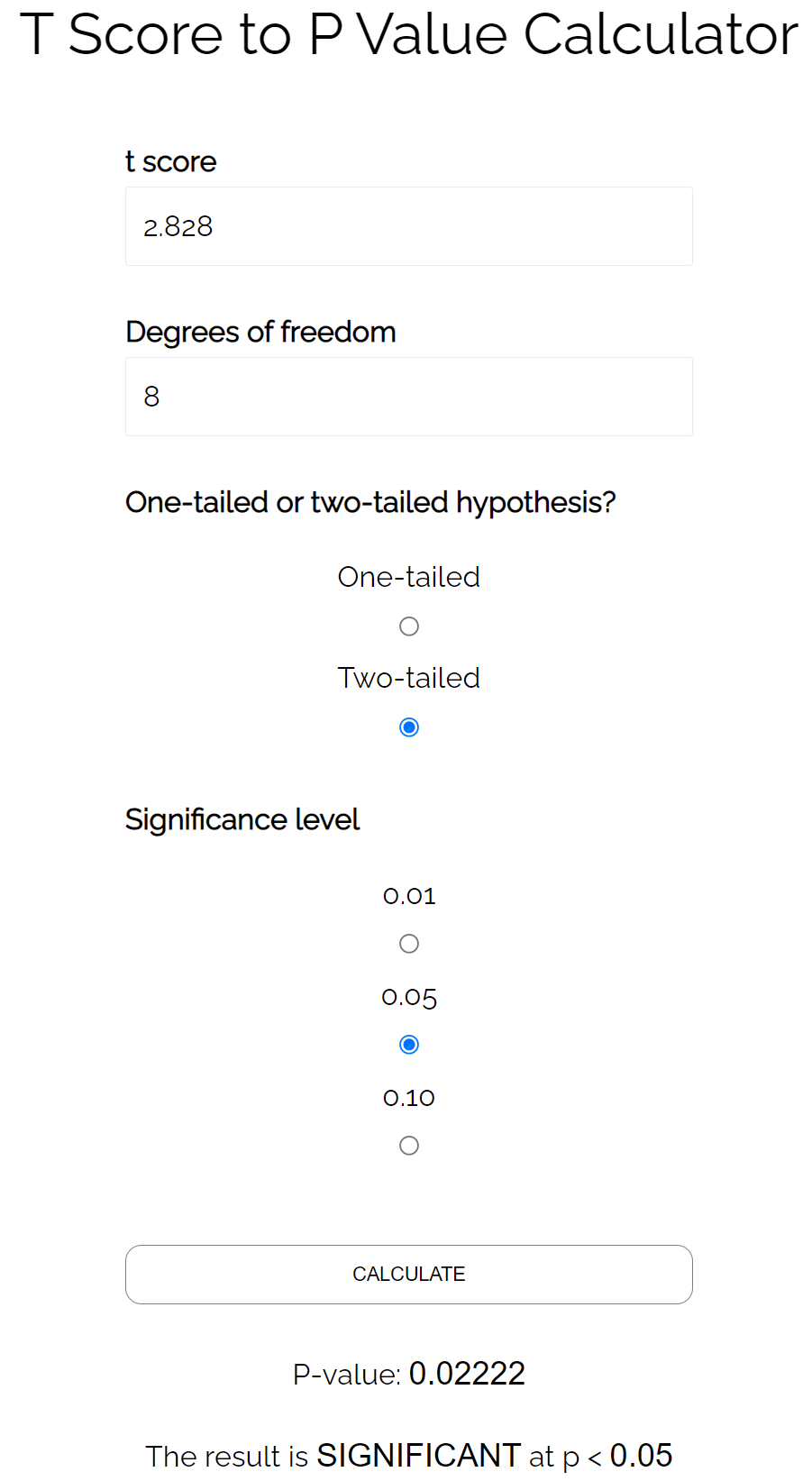
Omdat deze p-waarde kleiner is dan 0,05, kunnen we concluderen dat de correlatie tussen deze twee variabelen statistisch significant is.

Aanvullende bronnen

Hoe u een correlatietest uitvoert in Excel
Hoe u een correlatietest uitvoert in R
Wat wordt beschouwd als een ‘zwakke’ correlatie?
Wat wordt beschouwd als een “sterke” correlatie?