De t-test begrijpen bij lineaire regressie

Lineaire regressie wordt gebruikt om de relatie tussen een voorspellende variabele en een responsvariabele te kwantificeren.

Telkens wanneer we een lineaire regressie uitvoeren, willen we weten of er een statistisch significante relatie bestaat tussen de voorspellende variabele en de responsvariabele.

We testen op significantie door een t-test uit te voeren voor de regressiehelling. Voor deze t-toets gebruiken we de volgende nul- en alternatieve hypothese:

• H ₀ : β ₁ = 0 (de helling is gelijk aan nul)
• H _A : β ₁ ≠ 0 (de helling is niet gelijk aan nul)

Vervolgens berekenen we de teststatistiek als volgt:

t = b / SE _b

Goud:

• b : schatting van de coëfficiënt
• SE _b : standaardfout van de coëfficiëntschatting

Als de p-waarde die overeenkomt met t onder een bepaalde drempel ligt (bijvoorbeeld α = 0,05), dan verwerpen we de nulhypothese en concluderen we dat er een statistisch significante relatie bestaat tussen de voorspellende variabele en de responsvariabele.

Het volgende voorbeeld laat zien hoe u in de praktijk een t-toets voor een lineair regressiemodel uitvoert.

Voorbeeld: uitvoeren van een t-test voor lineaire regressie

Stel dat een hoogleraar voor veertig van zijn studenten de relatie tussen de gestudeerde uren en de examencijfers wil analyseren.

Het voert een eenvoudige lineaire regressie uit met bestudeerde uren als voorspellende variabele en ontvangen examenscores als responsvariabele.

De volgende tabel toont de resultaten van het regressiemodel:

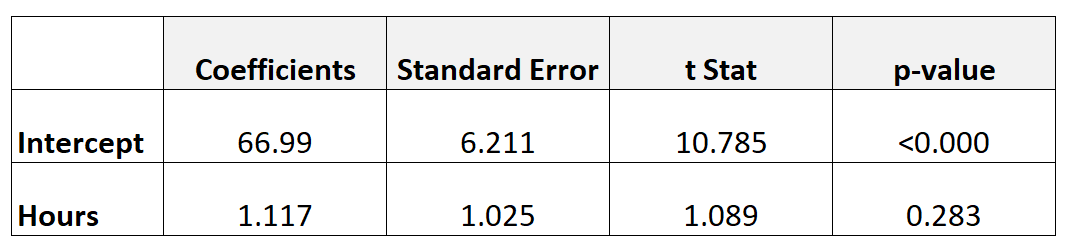
Om te bepalen of de bestudeerde uren een statistisch significante relatie hebben met het eindexamencijfer, kunnen we een t-toets uitvoeren.

Voor deze t-toets gebruiken we de volgende nul- en alternatieve hypothese:

• H ₀ : β ₁ = 0 (de helling van de bestudeerde uren is gelijk aan nul)
• H _A : β ₁ ≠ 0 (de helling van de bestudeerde uren is niet gelijk aan nul)

Vervolgens berekenen we de teststatistiek als volgt:

• t = b / SE _b
• t = 1,117 / 1,025
• t = 1,089

De p-waarde die overeenkomt met t = 1,089 met df = n-2 = 40 – 2 = 38 is 0,283 .

Merk op dat we ook de T-score naar P-waardecalculator kunnen gebruiken om deze p-waarde te berekenen:

Omdat deze p-waarde niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen.

Dit betekent dat de bestudeerde uren geen statistisch significante relatie hebben tussen de eindexamenresultaten.

Aanvullende bronnen

De volgende zelfstudies bieden aanvullende informatie over lineaire regressie:

Inleiding tot eenvoudige lineaire regressie
Inleiding tot meervoudige lineaire regressie
Hoe regressiecoëfficiënten te interpreteren
Hoe de F-test te interpreteren voor de algehele significantie in regressie