Hoe een t-test uit te voeren met ongelijke steekproefgroottes

Een vraag die studenten vaak stellen als het om statistiek gaat, is:

Is het mogelijk om een t-test uit te voeren als de steekproefomvang van elke groep niet gelijk is?

Het korte antwoord:

Ja, u kunt een t-test uitvoeren als de steekproefomvang niet gelijk is. Gelijke steekproefgroottes behoren niet tot de aannames die bij een t-test worden gedaan.

De echte problemen ontstaan wanneer de twee steekproeven geen gelijke varianties hebben, wat een van de aannames is die bij een t-toets worden gedaan.

Wanneer dit gebeurt, wordt aanbevolen om in plaats daarvan de t-test van Welch te gebruiken, die niet uitgaat van gelijke varianties.

De volgende voorbeelden laten zien hoe u T-toetsen kunt uitvoeren met ongelijke steekproefomvang wanneer de varianties gelijk zijn en wanneer niet.

Voorbeeld 1: Ongelijke steekproefomvang en gelijke varianties

Stel dat we twee programma’s beheren die zijn ontworpen om studenten te helpen beter te presteren op bepaalde examens.

De resultaten zijn als volgt:

Programma 1:

• n (steekproefgrootte): 500
• x (steekproefgemiddelde): 80
• s (steekproefstandaardafwijking): 5

Programma 2:

• n (steekproefgrootte): 20
• x (steekproefgemiddelde): 85
• s (steekproefstandaardafwijking): 5

De volgende code laat zien hoe u een boxplot in R maakt om de verdeling van examenscores voor elk programma te visualiseren:

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=5)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

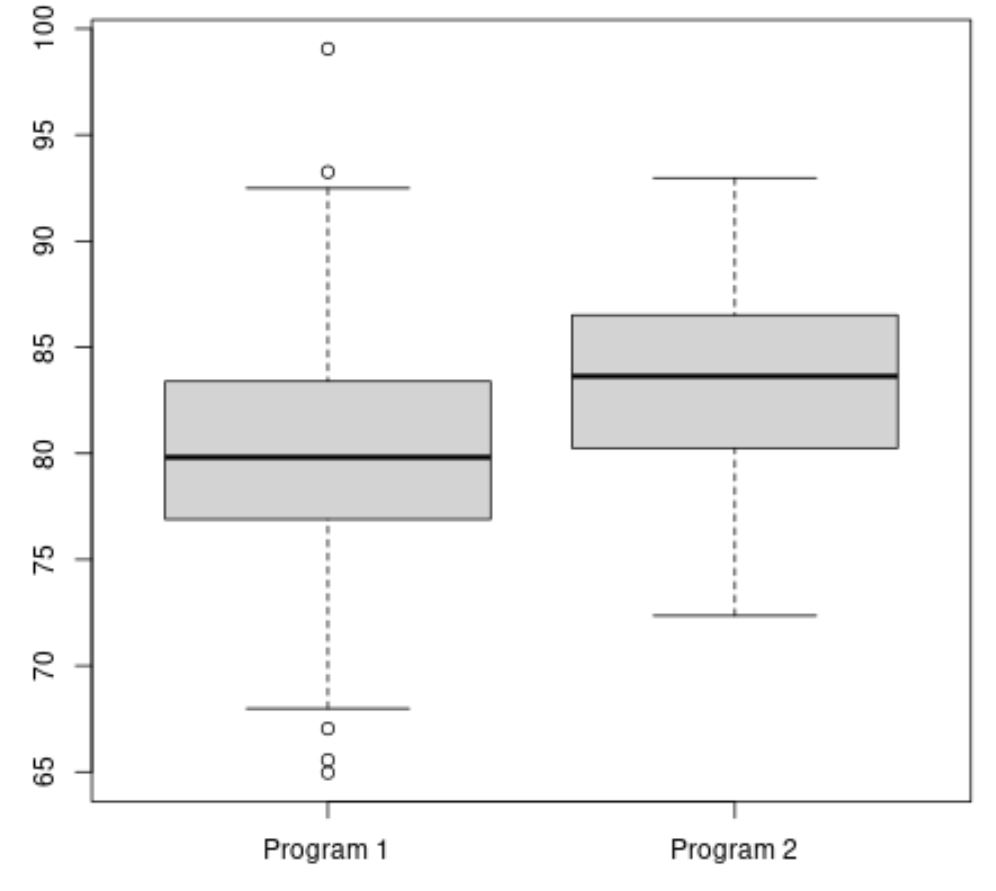
De gemiddelde examenscore voor Programma 2 lijkt hoger, maar de variantie in examenscores tussen beide opleidingen is ongeveer gelijk.

De volgende code laat zien hoe u een t-test van onafhankelijke monsters kunt uitvoeren met de t-test van Welch:

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -3.3348, df = 518, p-value = 0.0009148
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.111504 -1.580245
sample estimates:
mean of x mean of y 
 80.11322 83.95910

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -3.3735, df = 20.589, p-value = 0.00293
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.219551 -1.472199
sample estimates:
mean of x mean of y 
 80.11322 83.95910 

De t-test van de onafhankelijke monsters retourneert een p-waarde van 0,0009 en de t-test van Welch retourneert een p-waarde van 0,0029 .

Omdat de p-waarde van elke test kleiner is dan 0,05, zouden we de nulhypothese in elke test verwerpen en concluderen dat er een statistisch significant verschil bestaat in de gemiddelde examenscores tussen de twee programma’s.

Hoewel de steekproefomvang ongelijk is, retourneren de t-test van de onafhankelijke steekproeven en de t-test van Welch beide vergelijkbare resultaten, aangezien de twee steekproeven gelijke varianties hadden.

Voorbeeld 2: Ongelijke steekproefomvang en ongelijke varianties

Stel dat we twee programma’s beheren die zijn ontworpen om studenten te helpen beter te presteren op bepaalde examens.

De resultaten zijn als volgt:

Programma 1:

• n (steekproefgrootte): 500
• x (steekproefgemiddelde): 80
• s (steekproefstandaardafwijking): 25

Programma 2:

• n (steekproefgrootte): 20
• x (steekproefgemiddelde): 85
• s (steekproefstandaardafwijking): 5

De volgende code laat zien hoe u een boxplot in R maakt om de verdeling van examenscores voor elk programma te visualiseren:

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=25)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

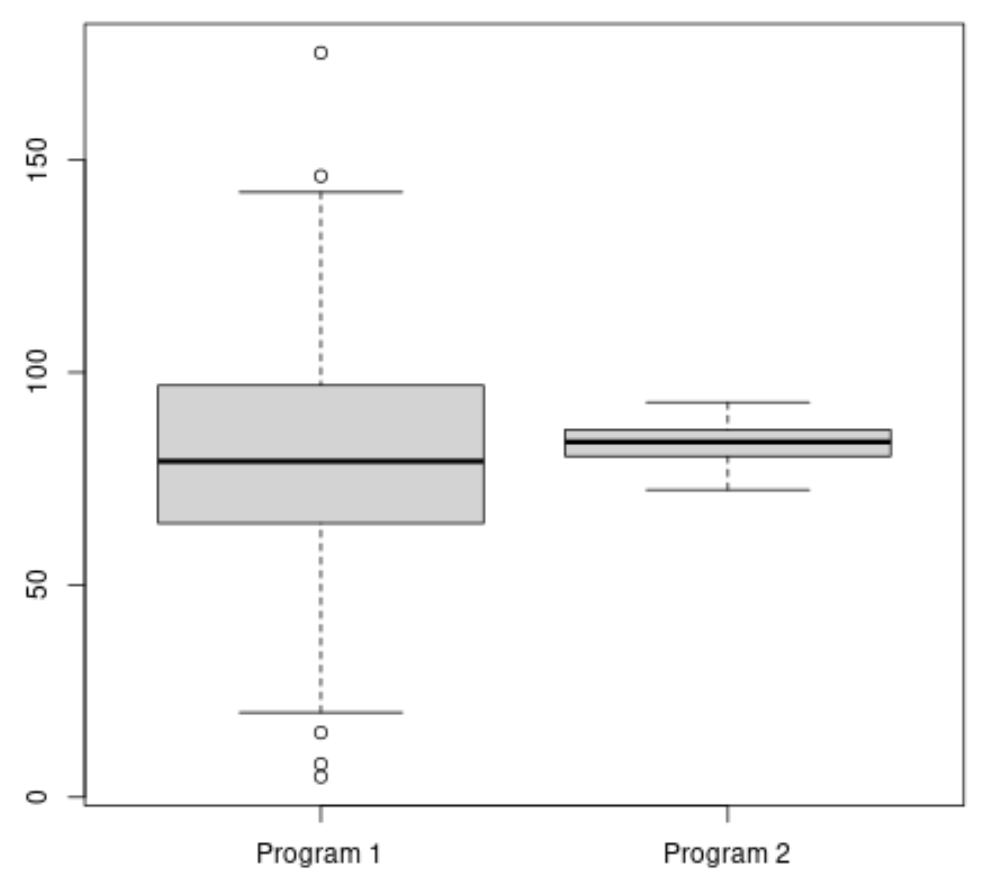
De gemiddelde examenscore voor Programma 2 lijkt hoger, maar de variantie van de examenscores voor Programma 1 is veel groter dan die voor Programma 2.

De volgende code laat zien hoe u een t-test van onafhankelijke monsters kunt uitvoeren met de t-test van Welch:

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -0.5988, df = 518, p-value = 0.5496
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -14.52474 7.73875
sample estimates:
mean of x mean of y 
  80.5661 83.9591

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -2.1338, df = 74.934, p-value = 0.03613
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.560690 -0.225296
sample estimates:
mean of x mean of y 
  80.5661 83.9591 

De t-test van de onafhankelijke monsters retourneert een p-waarde van 0,5496 en de t-test van Welch retourneert een p-waarde van 0,0361 .

De t-test van de onafhankelijke monsters kan geen verschil in gemiddelde examenscores detecteren, maar de t-test van Welch kan wel een statistisch significant verschil detecteren.

Omdat de twee steekproeven ongelijke varianties hadden, kon alleen de t-test van Welch het statistisch significante verschil in gemiddelde examenscores detecteren, aangezien deze test niet uitgaat van gelijke varianties tussen steekproeven .

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over t-toetsen:

Inleiding tot de one-sample t-test
Inleiding tot de t-test met twee steekproeven
Inleiding tot de t-test van gepaarde monsters