Hoe t-distributie in python te gebruiken

De t-verdeling is een waarschijnlijkheidsverdeling die vergelijkbaar is met de normale verdeling , behalve dat deze zwaardere „staarten“ heeft dan de normale verdeling.

Met andere woorden: er bevinden zich meer waarden in de verdeling aan de uiteinden dan in het midden vergeleken met de normale verdeling:

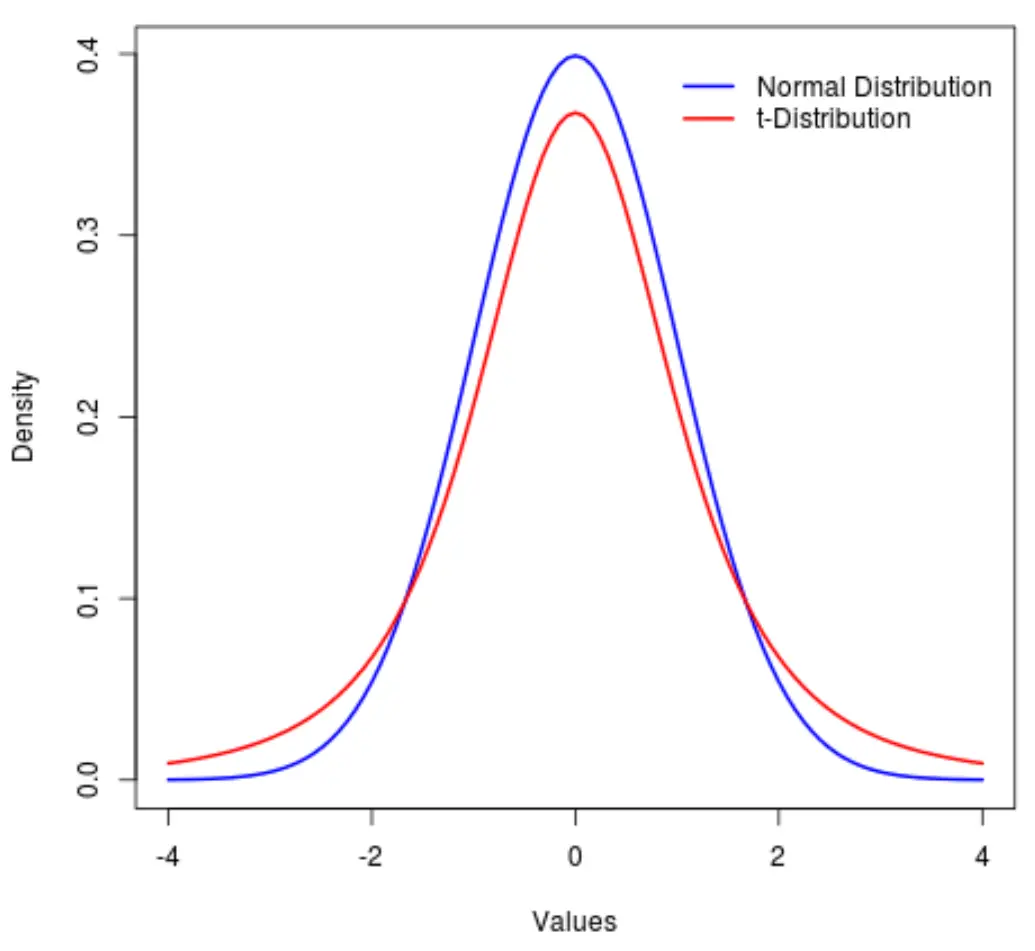
In deze tutorial wordt uitgelegd hoe je de t-distributie in Python gebruikt.

Hoe te genereren om te distribueren

U kunt de functie t.rvs(df, size) gebruiken om willekeurige waarden te genereren uit een verdeling met specifieke vrijheidsgraden en steekproefomvang:

 from scipy. stats import t

#generate random values from t distribution with df=6 and sample size=10
t. rvs (df= 6 , size= 10 )

array([-3.95799716, -0.01099963, -0.55953846, -1.53420055, -1.41775611,
       -0.45384974, -0.2767931, -0.40177789, -0.3602592, 0.38262431])

Het resultaat is een tabel met 10 waarden die elkaar opvolgen volgens een verdeling met 6 vrijheidsgraden.

Hoe P-waarden te berekenen met behulp van de t-verdeling

We kunnen de functie t.cdf(x, df, loc=0, scale=1) gebruiken om de p-waarde te vinden die is gekoppeld aan een t-toetsstatistiek.

Voorbeeld 1: Het vinden van een eenzijdige P-waarde

Stel dat we een eenzijdige hypothesetest uitvoeren en een teststatistiek van -1,5 en vrijheidsgraden = 10 krijgen.

We kunnen de volgende syntaxis gebruiken om de p-waarde te berekenen die overeenkomt met deze teststatistiek:

 from scipy. stats import t

#calculate p-value
t. cdf (x=-1.5, df=10)

0.08225366322272008

De eenzijdige p-waarde die overeenkomt met de teststatistiek van -1,5 met 10 vrijheidsgraden is 0,0822 .

Voorbeeld 2: Het vinden van een tweerichtings-P-waarde

Stel dat we een tweezijdige hypothesetest uitvoeren en een teststatistiek van 2,14 en vrijheidsgraden = 20 krijgen.

We kunnen de volgende syntaxis gebruiken om de p-waarde te berekenen die overeenkomt met deze teststatistiek:

 from scipy. stats import t

#calculate p-value
(1 - t. cdf (x=2.14, df=20)) * 2

0.04486555082549959

De tweezijdige p-waarde die overeenkomt met de teststatistiek van 2,14 met 20 vrijheidsgraden is 0,0448 .

Opmerking : u kunt deze antwoorden controleren met behulp van de inverse t-verdelingscalculator.

Hoe te herleiden tot distributie

U kunt de volgende syntaxis gebruiken om een verdeling met specifieke vrijheidsgraden te plotten:

 from scipy. stats import t
import matplotlib. pyplot as plt

#generate t distribution with sample size 10000
x = t. rvs (df= 12 , size= 10000 )

#create plot of t distribution
plt. hist (x, density= True , edgecolor=' black ', bins= 20 )

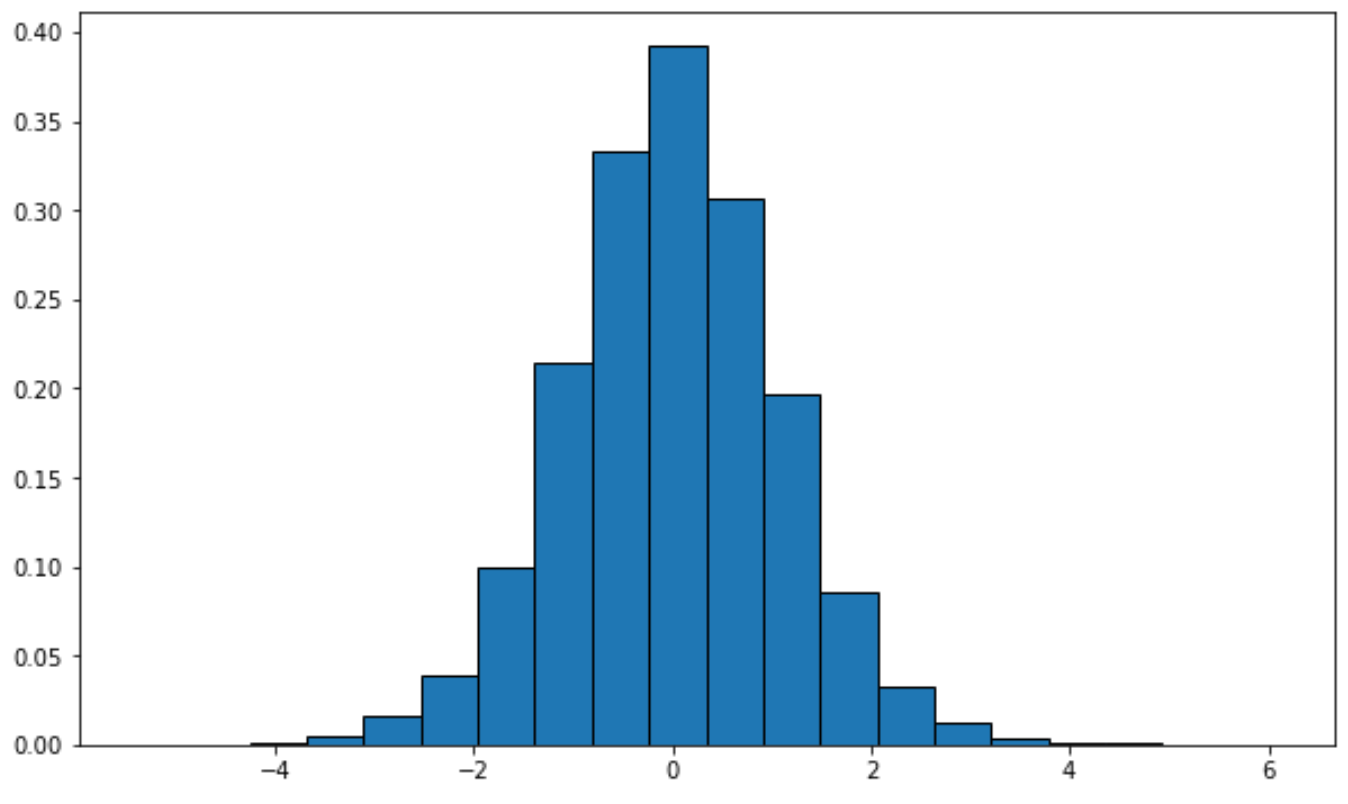
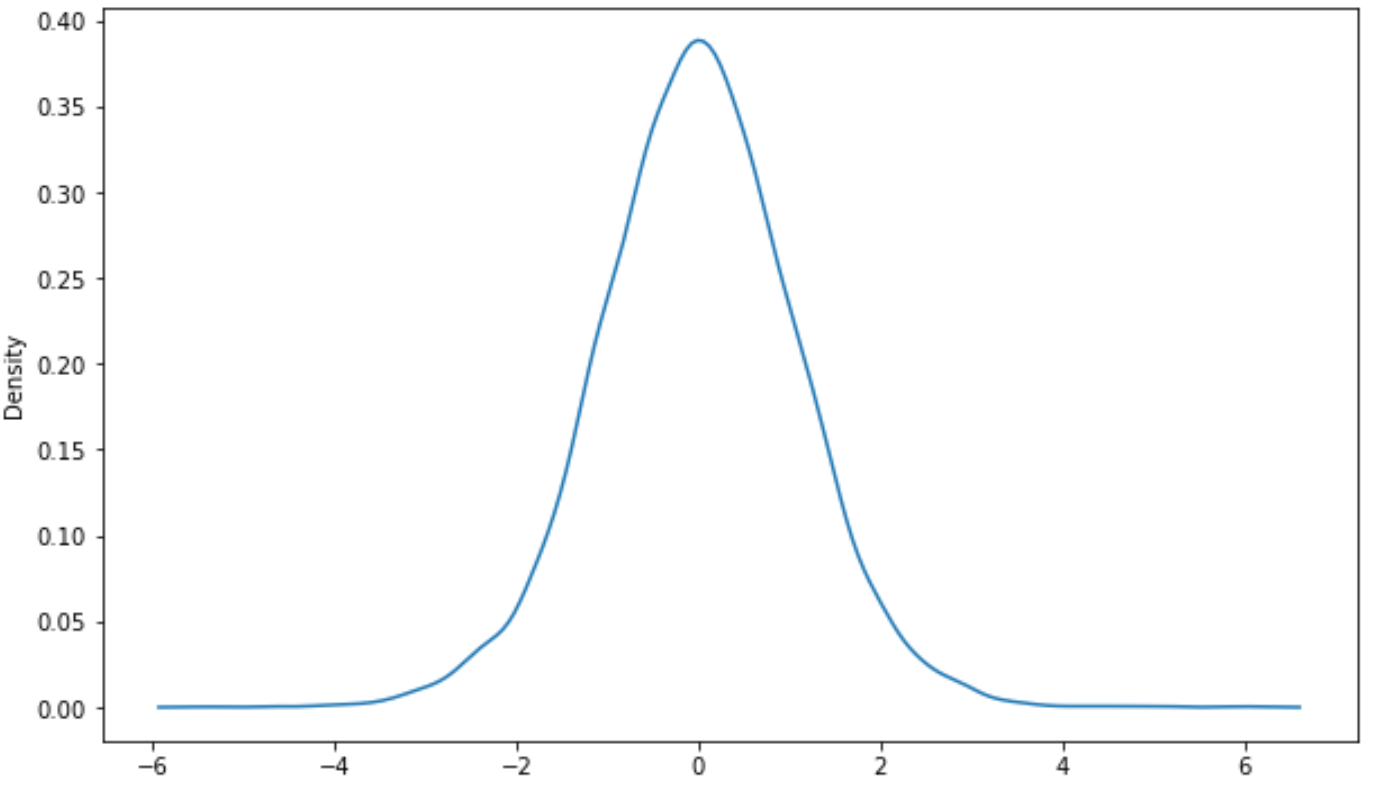
Als alternatief kunt u een dichtheidscurve maken met behulp van het Seaborn- visualisatiepakket:

 import seaborn as sns

#create density curve
sns. kdeplot (x)

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over de distributie:

Normale verdeling versus t-verdeling: wat is het verschil?
Inverse t-verdelingscalculator