T-score versus z-score: wanneer gebruik je ze?

Twee termen die studenten in statistiekcursussen vaak in verwarring brengen zijn t-scores en z-scores .

Beide worden veel gebruikt bij het testen van hypothesen of het construeren van betrouwbaarheidsintervallen , maar ze verschillen enigszins.

Hier is de formule voor elk:

score t = ( x – μ) / (s/√ n )

Goud:

• x : steekproefgemiddelde
• μ : Bevolkingsgemiddelde
• s : Standaarddeviatie van de steekproef
• n : Steekproefgrootte

z-score = ( x – μ) / σ

Goud:

• x : Ruwe gegevenswaarde
• μ : Bevolkingsgemiddelde
• σ : standaarddeviatie van de populatie

Dit stroomdiagram laat zien wanneer u ze allemaal moet gebruiken, op basis van uw gegevens:

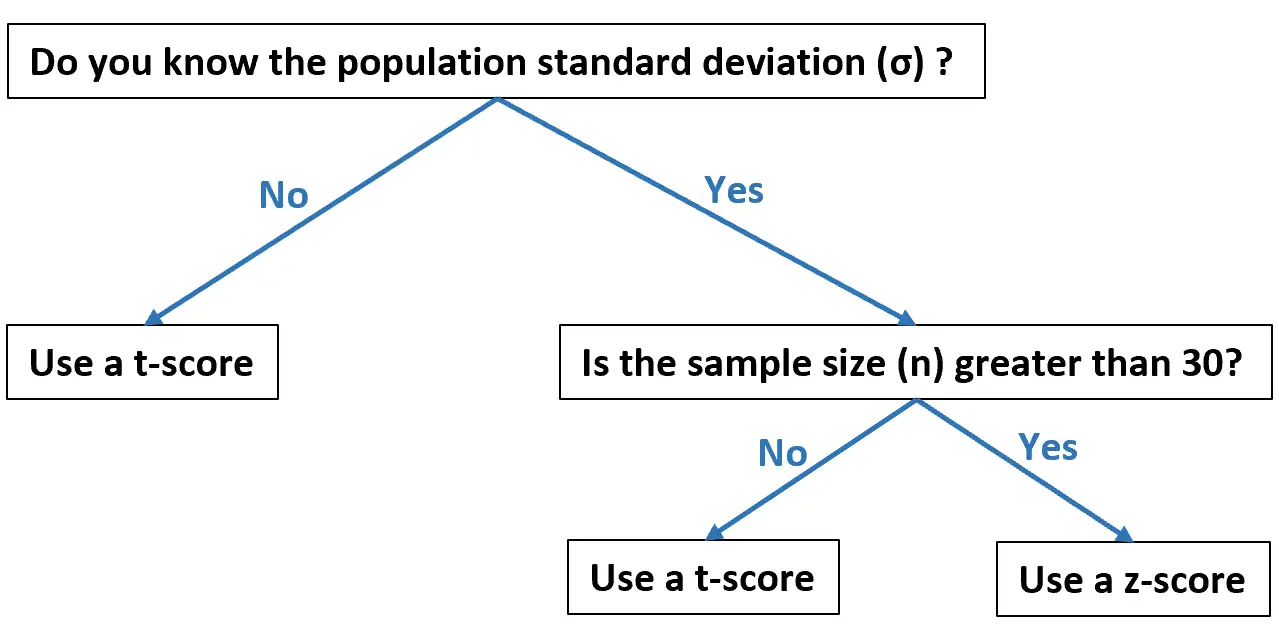
De volgende voorbeelden laten zien hoe u in de praktijk een T-score en een Z-score kunt berekenen.

Voorbeeld 1: Berekening van een T-Score

Stel dat een restaurant hamburgers bereidt met een gemiddeld gewicht van μ = 0,25 pond.

Stel dat we een willekeurige steekproef van n = 20 hamburgers nemen en vaststellen dat het gemiddelde gewicht van de steekproef x = 0,22 pond is met een standaarddeviatie van s = 0,05 pond. Voer een hypothesetest uit om te bepalen of het werkelijke gemiddelde gewicht van alle hamburgers die door dit restaurant worden geproduceerd gelijk is aan 0,25 pond.

Voor dit voorbeeld zouden we een T-score gebruiken om de hypothesetest uit te voeren, omdat aan geen van de volgende twee voorwaarden is voldaan.

• De populatiestandaarddeviatie (σ) is bekend. (σ is niet voorzien in dit voorbeeld)
• De steekproefomvang is groter dan 30. (n=20 in dit voorbeeld)

We zouden de t-score dus als volgt berekenen:

• score t = ( x – μ) / (s/√ n )
• t-score = (0,22 – 0,25) / (0,05 / √ 20 )
• t-score = -2,68

Volgens de P-waarde T-score calculator is de p-waarde die overeenkomt met deze t-score 0,01481 .

Omdat deze p-waarde kleiner is dan 0,05, hebben we voldoende bewijs om te zeggen dat het gemiddelde gewicht van de hamburgers die in dit restaurant worden geproduceerd niet gelijk is aan 0,25 pond.

Voorbeeld 2: Een Z-score berekenen

Stel dat een bedrijf batterijen produceert waarvan bekend is dat de levensduur een normale verdeling volgt met een gemiddelde van μ = 20 uur en een standaardafwijking van σ = 5 uur.

Stel dat we een willekeurige steekproef van n = 50 batterijen nemen en vaststellen dat het steekproefgemiddelde x = 21 uur is. Voer een hypothesetest uit om te bepalen of de werkelijke gemiddelde levensduur van alle door dit bedrijf geproduceerde batterijen gelijk is aan 20 uur.

Voor dit voorbeeld zouden we een z-score gebruiken om de hypothesetest uit te voeren, omdat aan beide volgende voorwaarden is voldaan:

• De populatiestandaarddeviatie (σ) is bekend. (σ is in dit voorbeeld gelijk aan 5)
• De steekproefomvang is groter dan 30. (n=50 in dit voorbeeld)

We zouden de z-score dus als volgt berekenen:

• z-score = ( x – μ) / σ
• z-score = (21 – 20) / 5
• z-score = 0,2

Volgens de P-waarde Z-score-calculator is de p-waarde die overeenkomt met deze z-score 0,84184 .

Aangezien deze p-waarde niet minder dan 0,05 bedraagt, hebben we niet voldoende bewijs om te zeggen dat de gemiddelde levensduur van alle door dit bedrijf vervaardigde batterijen niet meer dan 20 uur bedraagt.

Aanvullende bronnen

De volgende tutorials bieden meer informatie over T-scores en Z-scores:

Normale verdeling versus t-verdeling: wat is het verschil?
Hoe leest u de verdelingstabel t
Hoe de Z-tabel te lezen