Het verschil tussen t-waarden en p-waarden in statistieken

Twee termen die studenten in de statistiek vaak verwarren zijn t-waarden en p-waarden .

Om het verschil tussen deze termen te begrijpen, helpt het om t-toetsen te begrijpen.

Over het algemeen zijn er drie verschillende soorten t-toetsen:

• One-sample t-test : wordt gebruikt om te testen of een populatiegemiddelde gelijk is aan een bepaalde waarde.
• T-test met twee steekproeven : wordt gebruikt om te testen of de gemiddelden van twee populaties gelijk zijn.
• T-test voor gepaarde steekproeven : wordt gebruikt om te testen of de gemiddelden van twee populaties gelijk zijn wanneer elke waarneming in het ene monster kan worden geassocieerd met een waarneming in het andere monster.

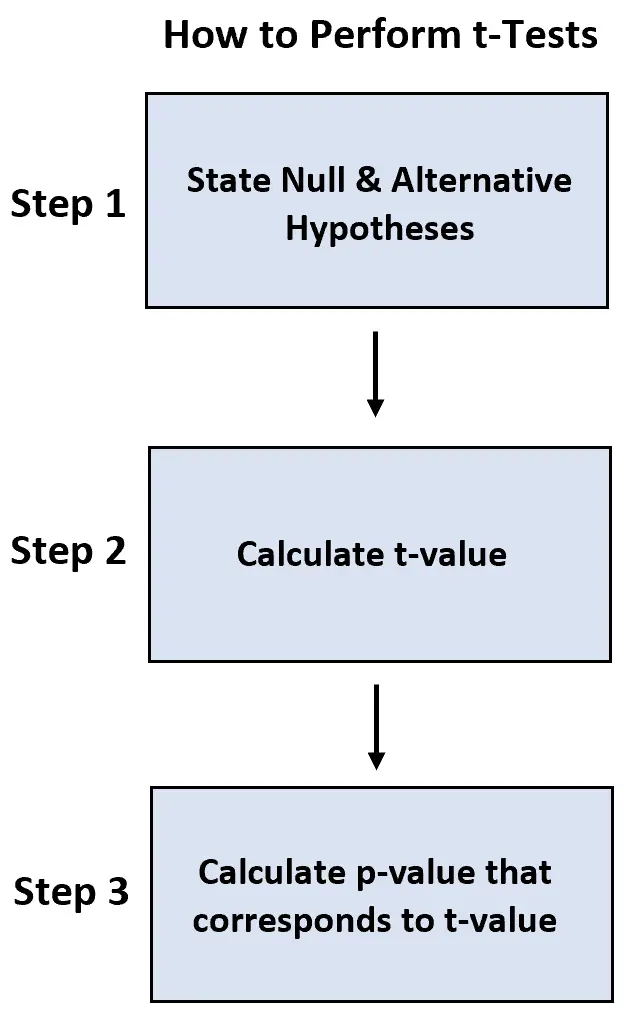
We gebruiken de volgende stappen om elke test uit te voeren:

• Stap 1: Formuleer de nul- en alternatieve hypothese.
• Stap 2: Bereken de t-waarde.
• Stap 3: Bereken de p-waarde die overeenkomt met de t-waarde.

Voor elke test is de t-waarde een manier om het verschil tussen populatiegemiddelden te kwantificeren, en de p-waarde is de kans op het verkrijgen van een t-waarde met een absolute waarde die minstens zo groot is als we feitelijk in de steekproef hebben waargenomen. gegevens als de nulhypothese daadwerkelijk waar is.

Als de p-waarde kleiner is dan een bepaalde waarde (bijvoorbeeld 0,05), dan verwerpen we de nulhypothese van de test.

Voor elk type t-toets zijn we geïnteresseerd in de p-waarde en gebruiken we de t-waarde eenvoudigweg als tussenstap om de p-waarde te berekenen.

Het volgende voorbeeld laat zien hoe u een t-waarde en de bijbehorende p-waarde voor een t-toets met twee steekproeven kunt berekenen en interpreteren.

Voorbeeld: Bereken en interpreteer T-waarden en P-waarden

Stel dat we willen weten of het gemiddelde gewicht van twee verschillende soorten schildpadden gelijk is of niet. We verzamelen een eenvoudige willekeurige steekproef van 12 schildpadden uit elke populatie met de volgende gewichten:

Soort #1 : 301, 298, 295, 297, 304, 305, 309, 298, 291, 299, 293, 304

Soort #2 : 302, 309, 324, 313, 312, 310, 305, 298, 299, 300, 289, 294

U kunt als volgt een t-test met twee steekproeven uitvoeren met behulp van deze gegevens:

Stap 1: Formuleer de nul- en alternatieve hypothese.

Eerst zullen we de nul- en alternatieve hypothesen formuleren:

• H ₀ : μ ₁ = μ ₂ (de twee populatiegemiddelden zijn gelijk)
• H ₁ : μ ₁ ≠ μ ₂ (de twee populatiegemiddelden zijn niet gelijk)

Stap 2: Bereken de t-waarde.

Vervolgens voeren we de gewichten van elk schildpadmonster in de t-testcalculator met twee monsters in en ontdekken dat de t-waarde -1,608761 is.

Stap 3: Bereken de p-waarde.

We kunnen ook de t-testcalculator met twee steekproeven gebruiken om te ontdekken dat de p-waarde die overeenkomt met een t-waarde van -1,608761 0,121926 is.

Omdat deze p-waarde niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen.

Dit betekent dat we niet voldoende bewijs hebben om te zeggen dat het gemiddelde gewicht van schildpadden tussen de twee populaties verschillend is.

Merk op dat we eenvoudigweg de t-waarde als tussenstap hebben gebruikt om de p-waarde te berekenen. De p-waarde is de werkelijke waarde waarin we geïnteresseerd waren, maar we moesten eerst de t-waarde berekenen.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over t-toetsen en p-waarden:

Een inleiding tot de one-sample t-test
Een inleiding tot de t-toets met twee steekproeven
Een inleiding tot de t-test van gepaarde monsters
Hoe u handmatig een P-waarde kunt berekenen op basis van een t-toets