Hoe de scheffe-test uit te voeren in r

Een eenrichtings-ANOVA wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.

Als de totale p-waarde van de ANOVA-tabel onder een bepaald significantieniveau ligt, hebben we voldoende bewijs om te zeggen dat ten minste één van de groepsgemiddelden verschilt van de andere.

Dit vertelt ons echter niet welke groepen van elkaar verschillen. Dit vertelt ons eenvoudigweg dat niet alle groepsgemiddelden gelijk zijn.

Om precies te weten welke groepen van elkaar verschillen, moeten we eenpost-hoc test uitvoeren die het foutenpercentage per gezin kan controleren.

Een van de meest gebruikte post-hoc-tests is de Scheffe-test.

In deze tutorial wordt uitgelegd hoe u de Scheffe-test uitvoert in R.

Voorbeeld: Scheffe-test in R

Stel dat een docent wil weten of drie verschillende studietechnieken al dan niet tot verschillende toetsscores bij studenten leiden. Om dit te testen wijst ze willekeurig 10 studenten toe om elke studietechniek te gebruiken en registreert ze hun examenresultaten.

We kunnen de volgende stappen in R gebruiken om een eenrichtings-ANOVA uit te voeren om te testen op verschillen in gemiddelde examenscores tussen de drie groepen, en de Scheffe-test gebruiken om precies te bepalen welke groepen verschillend zijn.

Stap 1: Maak de gegevensset.

De volgende code laat zien hoe u een dataset maakt met de examenresultaten van alle 30 studenten:

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

Stap 2: Bekijk de examenresultaten voor elke groep.

De volgende code laat zien hoe u boxplots kunt maken om de verdeling van de examenresultaten voor elke groep te visualiseren:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

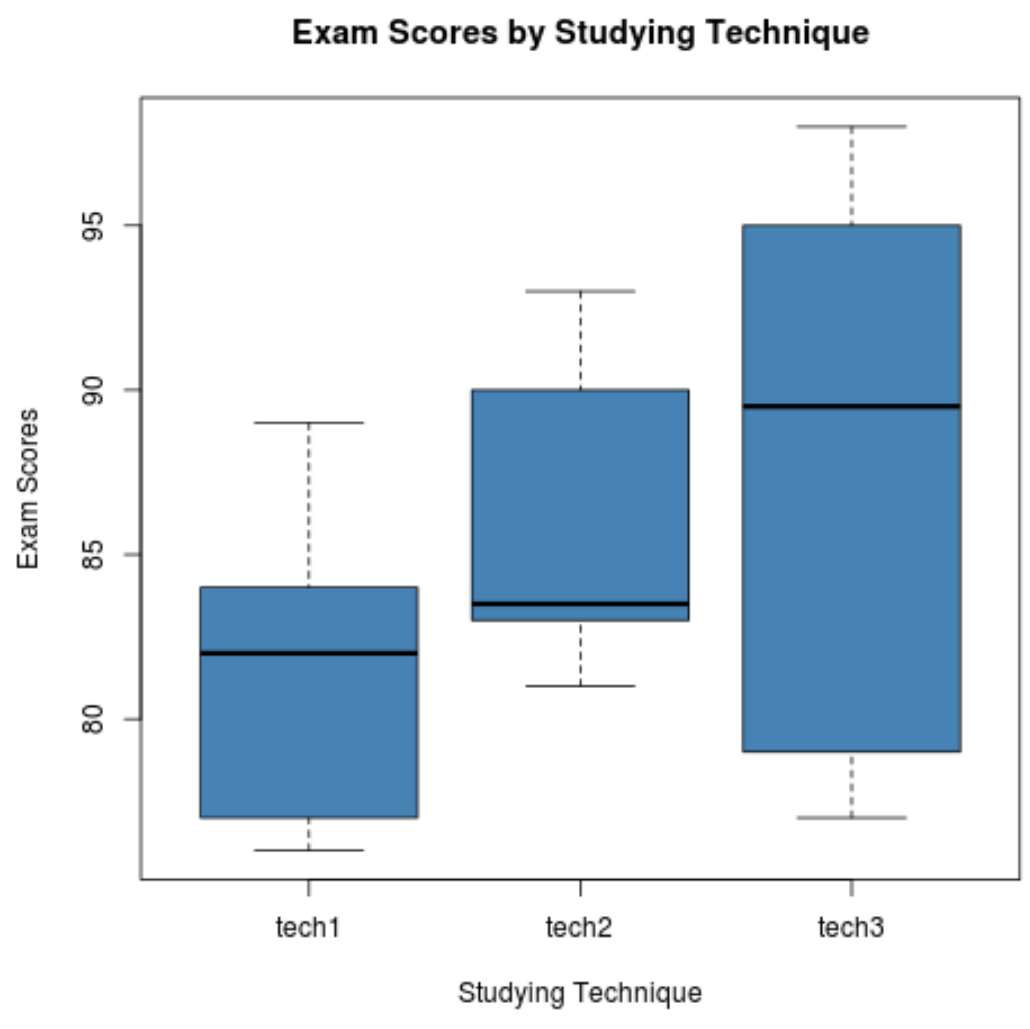
Stap 3: Voer een eenrichtings-ANOVA uit.

De volgende code laat zien hoe u een eenrichtings-ANOVA uitvoert om te testen op verschillen tussen de gemiddelde examenscores in elke groep:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Aangezien de totale p-waarde ( 0,0476 ) kleiner is dan 0,05, geeft dit aan dat niet elke groep dezelfde gemiddelde examenscore heeft.

Vervolgens voeren we de Scheffe-test uit om te bepalen welke groepen verschillend zijn.

Stap 4: Voer de Scheffe-test uit.

Om de Scheffe-test uit te voeren, zullen we de functie ScheffeTest() uit het DescTools- pakket gebruiken.

De volgende code laat zien hoe u deze functie voor ons voorbeeld kunt gebruiken:

 #load DescTools package
library(DescTools)

#perform Scheffe's test
ScheffeTest(model)

  Posthoc multiple comparisons of means: Scheffe Test 
    95% family-wise confidence level

$technical
            diff lwr.ci upr.ci pval    
tech2-tech1 4.2 -2.24527202 10.645272 0.2582    
tech3-tech1 6.4 -0.04527202 12.845272 0.0519 .  
tech3-tech2 2.2 -4.24527202 8.645272 0.6803    

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

De manier om het resultaat te interpreteren is als volgt:

• Het gemiddelde verschil in examenuitslag tussen techniek 2 en techniek 1 bedraagt 4,2 . De overeenkomstige p-waarde voor het gemiddelde verschil is 0,2582 .
• Het gemiddelde verschil in examenuitslag tussen techniek 3 en techniek 1 bedraagt 6,4 . De overeenkomstige p-waarde voor het gemiddelde verschil is 0,0519 .
• Het gemiddelde verschil in examenuitslag tussen techniek 3 en techniek 2 bedraagt 2,2 . De overeenkomstige p-waarde voor het gemiddelde verschil is 0,6803 .

Afhankelijk van het significantieniveau dat we besluiten te gebruiken, zijn Techniek 3 en Techniek 1 de enige twee groepen die statistisch significant verschillend lijken.

Aanvullende bronnen

Eenrichtings-ANOVA uitvoeren in R
Hoe de Tukey-test uit te voeren in R
Een Bonferroni-correctie uitvoeren in R