Hoe kwadratische regressie uit te voeren op een ti-84-rekenmachine

Wanneer twee variabelen een lineair verband hebben, kunnen we vaak eenvoudige lineaire regressie gebruiken om hun verband te kwantificeren.

Wanneer twee variabelen echter een kwadratische relatie hebben, kunnen we kwadratische regressie gebruiken om hun relatie te kwantificeren.

In deze tutorial wordt uitgelegd hoe u kwadratische regressie uitvoert op een TI-84-rekenmachine.

Voorbeeld: kwadratische regressie op een TI-84-rekenmachine

Stel dat we de relatie tussen het aantal gewerkte uren en geluk willen begrijpen. We hebben de volgende gegevens over het aantal gewerkte uren per week en het gerapporteerde geluksniveau (op een schaal van 0 tot 100) voor 11 verschillende mensen:

Volg de volgende stappen om kwadratische regressie uit te voeren op een TI-84-rekenmachine.

Stap 1: Visualiseer de gegevens.

Voordat we kwadratische regressie kunnen gebruiken, moeten we ervoor zorgen dat de relatie tussen de verklarende variabele (uren) en de responsvariabele (geluk) inderdaad kwadratisch is.

Eerst voeren we de gegevenswaarden in voor de verklarende variabele en de responsvariabele. Druk op Stat en vervolgens op BEWERKEN . Vul de volgende waarden in voor de verklarende variabele (gewerkte uren) in kolom L1 en de waarden voor de responsvariabele (geluk) in kolom L2:

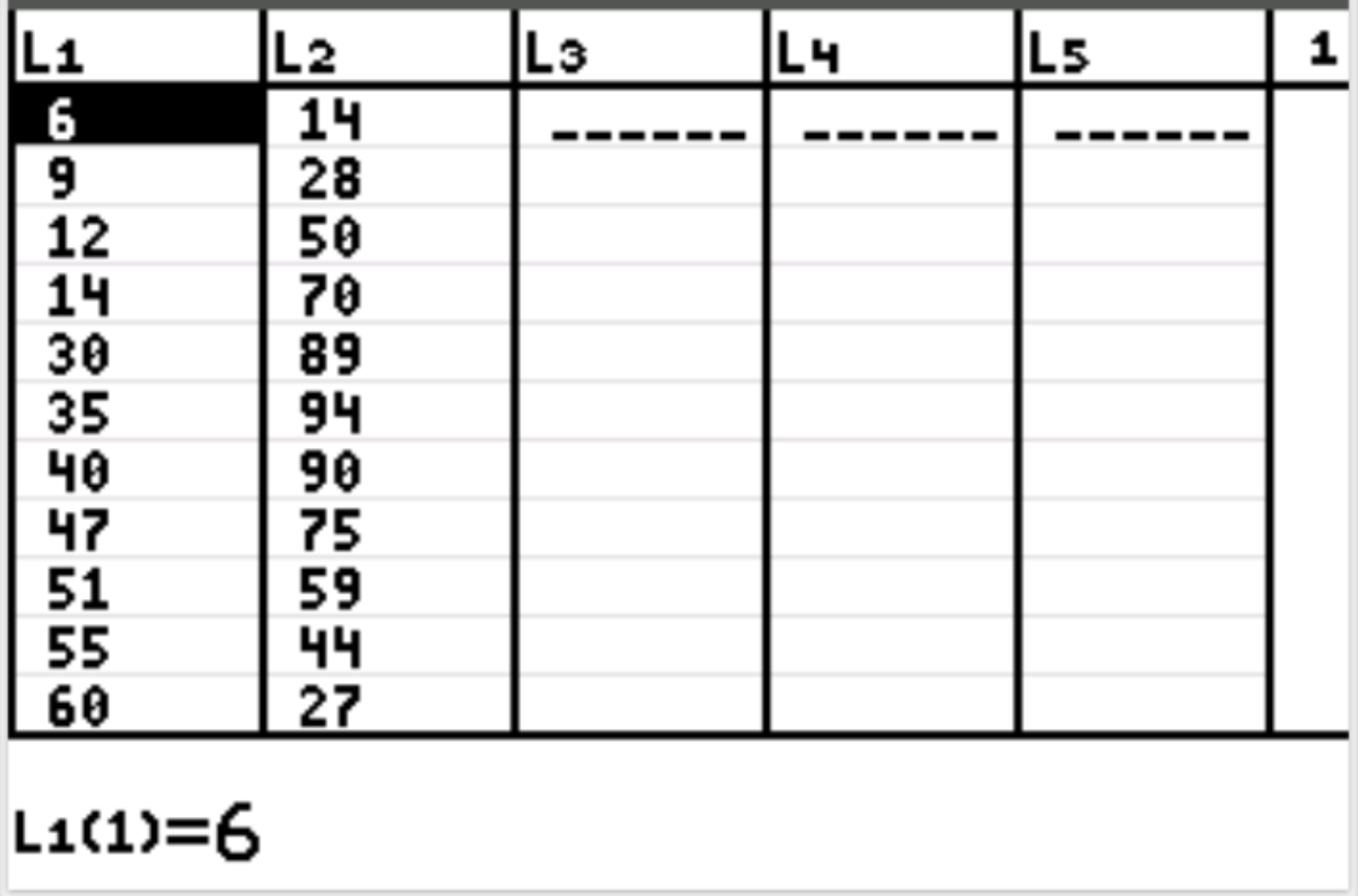
Druk vervolgens op 2nd en vervolgens op y= om het statplot- menu te openen. Markeer Plot1 en druk op Enter . Zorg ervoor dat plotten is ingeschakeld en dat L1 en L2 zijn geselecteerd voor respectievelijk Xlist en Ylist:

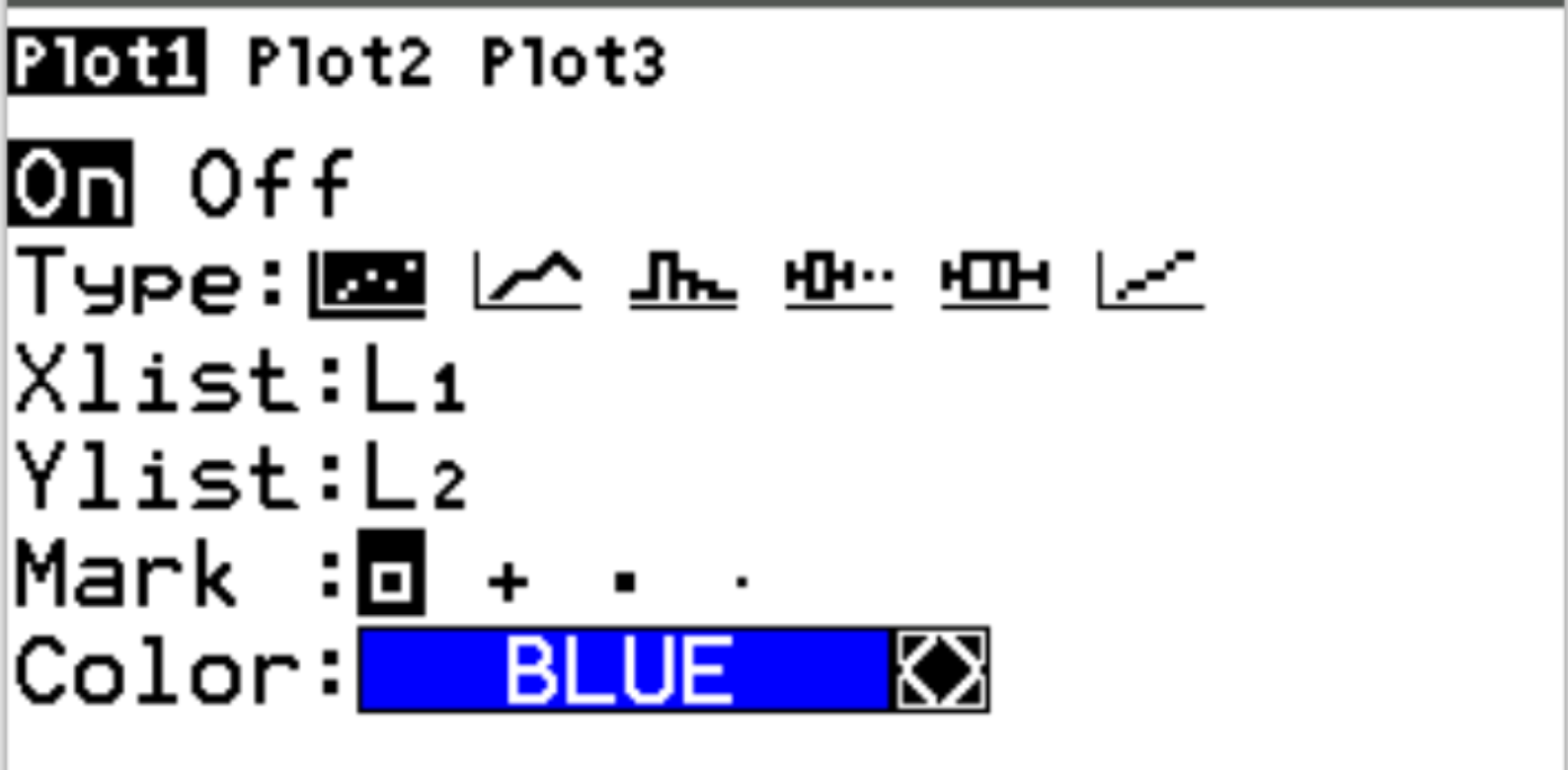
Druk vervolgens op zoom en vervolgens op 9:ZoomStat . Dit levert automatisch de volgende puntenwolk op:

We kunnen zien dat het geluk de neiging heeft toe te nemen naarmate het aantal gewerkte uren toeneemt van nul tot een bepaald punt, maar vervolgens begint af te nemen naarmate het aantal gewerkte uren verder toeneemt.

Deze omgekeerde ‚U‘-vorm in het spreidingsdiagram geeft aan dat er een kwadratische relatie bestaat tussen gewerkte uren en geluk, wat betekent dat we kwadratische regressie moeten gebruiken om deze relatie te kwantificeren.

Stap 2: Voer kwadratische regressie uit.

Vervolgens zullen we een kwadratische regressie uitvoeren. Druk op Stat en scroll vervolgens naar CALC . Blader vervolgens naar 5:QuadReg en druk op Enter .

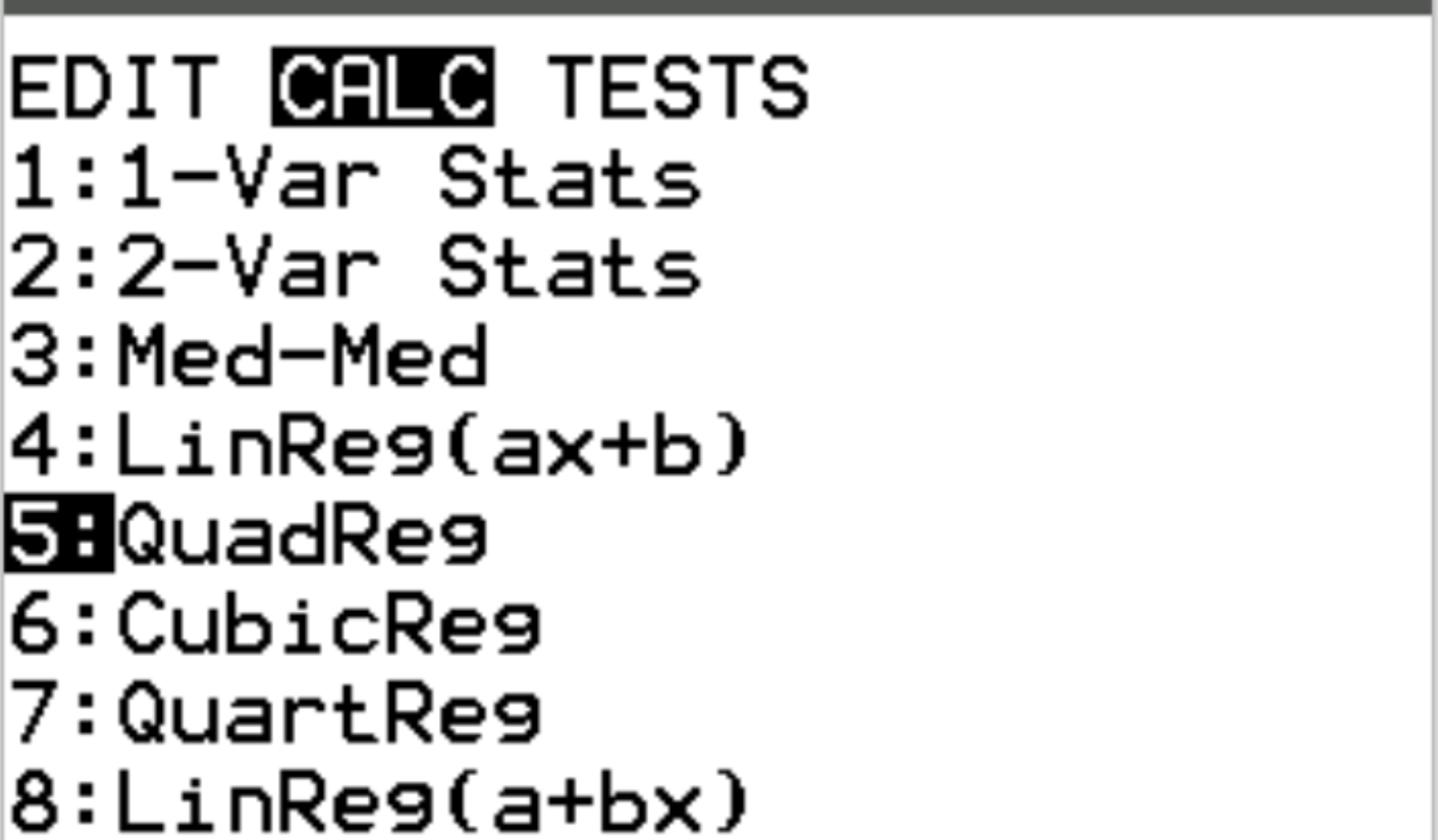
Zorg ervoor dat voor Xlist en Ylist L1 en L2 zijn geselecteerd, aangezien dit de kolommen zijn die we hebben gebruikt om onze gegevens in te voeren. Laat FreqList leeg. Blader omlaag naar Bereken en druk op Enter .

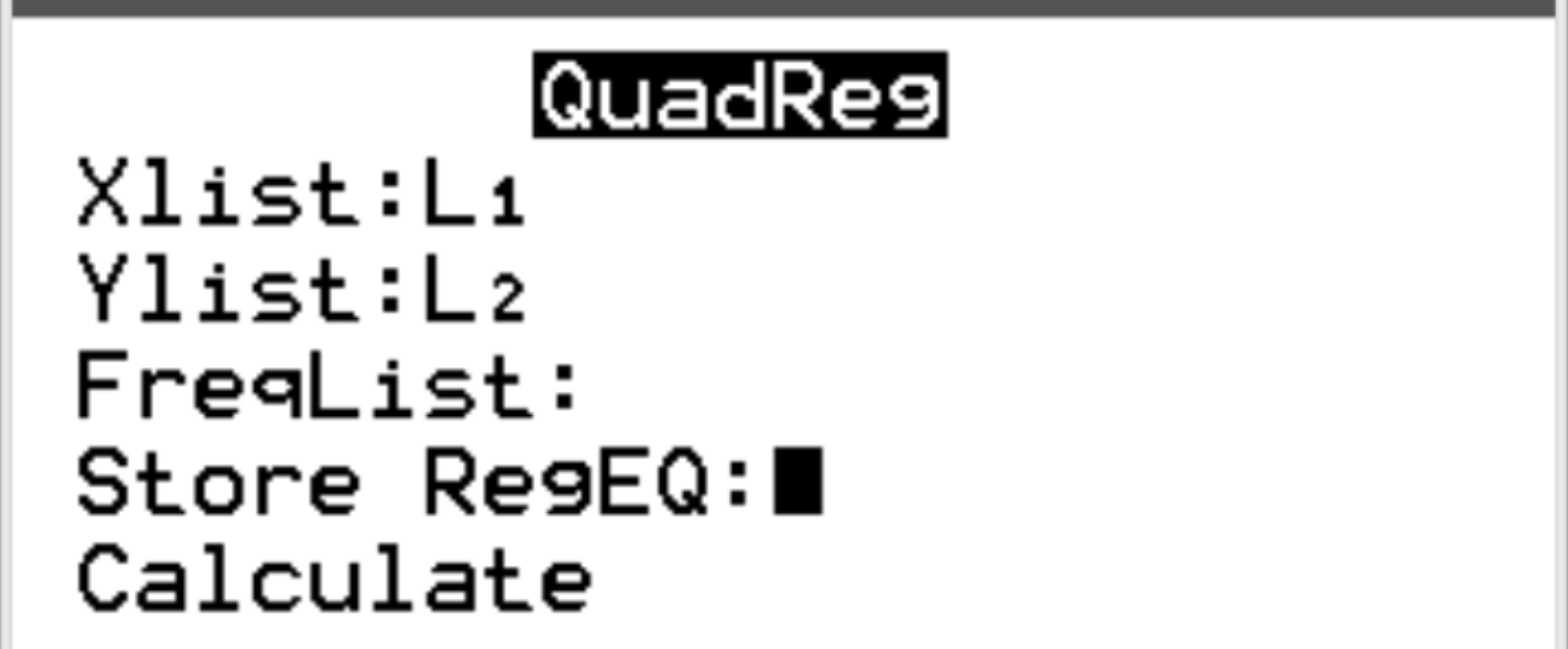
De volgende uitvoer verschijnt automatisch:

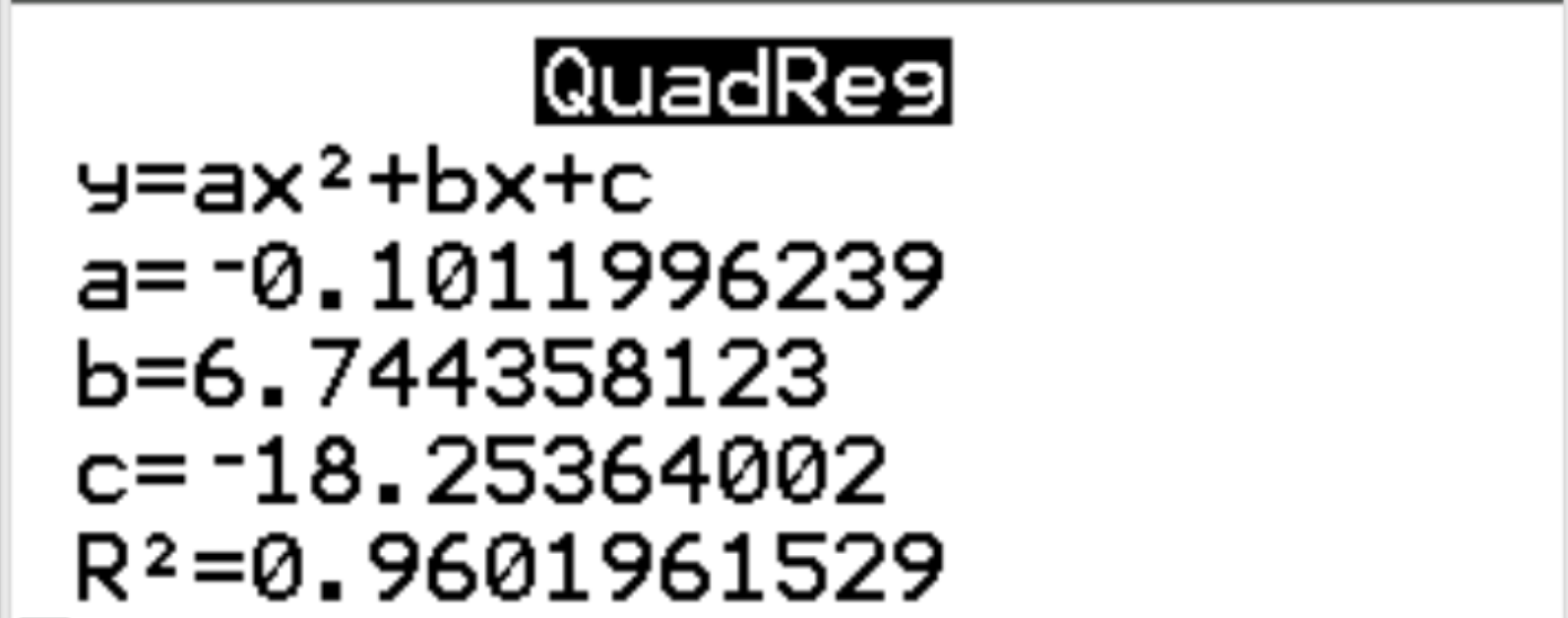
Stap 3: Interpreteer het resultaat.

Uit de resultaten kunnen we zien dat de geschatte regressievergelijking is:

geluk = -0,1012 (uren) ² + 6,7444 (uren) – 18,2536

We kunnen deze vergelijking gebruiken om het voorspelde geluk van een individu te vinden, gegeven het aantal uren dat hij of zij per week werkt.

Een persoon die bijvoorbeeld 60 uur per week werkt, zou een geluksniveau van 22,09 hebben:

geluk = -0,1012(60) ² + 6,7444(60) – 18,2536 = 22,09

Omgekeerd zou iemand die 30 uur per week werkt een geluksniveau van 92,99 moeten hebben:

geluk = -0,1012(30) ² + 6,7444(30) – 18,2536 = 92,99

We kunnen ook zien dat de r kwadraat voor het regressiemodel r ² = 0,9602 is. Dit is het deel van de variantie in de responsvariabele dat kan worden verklaard door de verklarende variabelen. In dit voorbeeld kan 96,02% van de variatie in geluk verklaard worden door uren en tijden ² .