Ridge-regressie in r (stap voor stap)

Ridge-regressie is een methode die we kunnen gebruiken om een regressiemodel te fitten wanneer multicollineariteit in de gegevens aanwezig is.

In een notendop probeert regressie met de kleinste kwadraten coëfficiëntschattingen te vinden die de resterende som van de kwadraten (RSS) minimaliseren:

RSS = Σ(y _i – ŷ _i )2

Goud:

• Σ : Een Grieks symbool dat som betekent
• y _i : de werkelijke responswaarde voor de ^i-de waarneming
• ŷ _i : De voorspelde responswaarde op basis van het meervoudige lineaire regressiemodel

Omgekeerd probeert nokregressie het volgende te minimaliseren:

RSS + λΣβ _j ²

waarbij j van 1 naar p voorspellende variabelen gaat en λ ≥ 0.

Deze tweede term in de vergelijking staat bekend als de opnameboete . Bij nokregressie selecteren we een waarde voor λ die de laagst mogelijke MSE-test oplevert (gemiddelde kwadratische fout).

Deze zelfstudie biedt een stapsgewijs voorbeeld van het uitvoeren van ridge-regressie in R.

Stap 1: Gegevens laden

Voor dit voorbeeld gebruiken we de ingebouwde dataset van R, genaamd mtcars . We zullen hp gebruiken als de responsvariabele en de volgende variabelen als voorspellers:

• mpg
• gewicht
• shit
• qsec

Om ridge-regressie uit te voeren, zullen we functies uit het glmnet- pakket gebruiken. Dit pakket vereist dat de responsvariabele een vector is en dat de set voorspellende variabelen van de klasse data.matrix is.

De volgende code laat zien hoe u onze gegevens kunt definiëren:

 #define response variable
y <- mtcars$hp

#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])

Stap 2: Pas het Ridge Regressiemodel toe

Vervolgens zullen we de functie glmnet() gebruiken om in het Ridge-regressiemodel te passen en alpha=0 te specificeren.

Houd er rekening mee dat het instellen van alfa op 1 gelijk is aan het gebruik van Lasso-regressie en het instellen van alfa op een waarde tussen 0 en 1 gelijk is aan het gebruik van een elastisch net.

Merk ook op dat nokregressie vereist dat de gegevens zodanig worden gestandaardiseerd dat elke voorspellende variabele een gemiddelde van 0 en een standaarddeviatie van 1 heeft.

Gelukkig doet glmnet() deze standaardisatie automatisch voor je. Als u de variabelen al hebt gestandaardiseerd, kunt u standardize=False opgeven.

 library (glmnet)

#fit ridge regression model
model <- glmnet(x, y, alpha = 0 )

#view summary of model
summary(model)

          Length Class Mode   
a0 100 -none- numeric
beta 400 dgCMatrix S4     
df 100 -none- numeric
dim 2 -none- numeric
lambda 100 -none- numeric
dev.ratio 100 -none- numeric
nulldev 1 -none- numeric
npasses 1 -none- numeric
jerr 1 -none- numeric
offset 1 -none- logical
call 4 -none- call   
nobs 1 -none- numeric

Stap 3: Kies een optimale waarde voor Lambda

Vervolgens zullen we de lambdawaarde identificeren die de laagste testgemiddelde kwadratische fout (MSE) oplevert met behulp van k-voudige kruisvalidatie .

Gelukkig heeft glmnet de functie cv.glmnet() die automatisch k-voudige kruisvalidatie uitvoert met behulp van k = 10 keer.

 #perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 0 )

#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda

[1] 10.04567

#produce plot of test MSE by lambda value
plot(cv_model) 

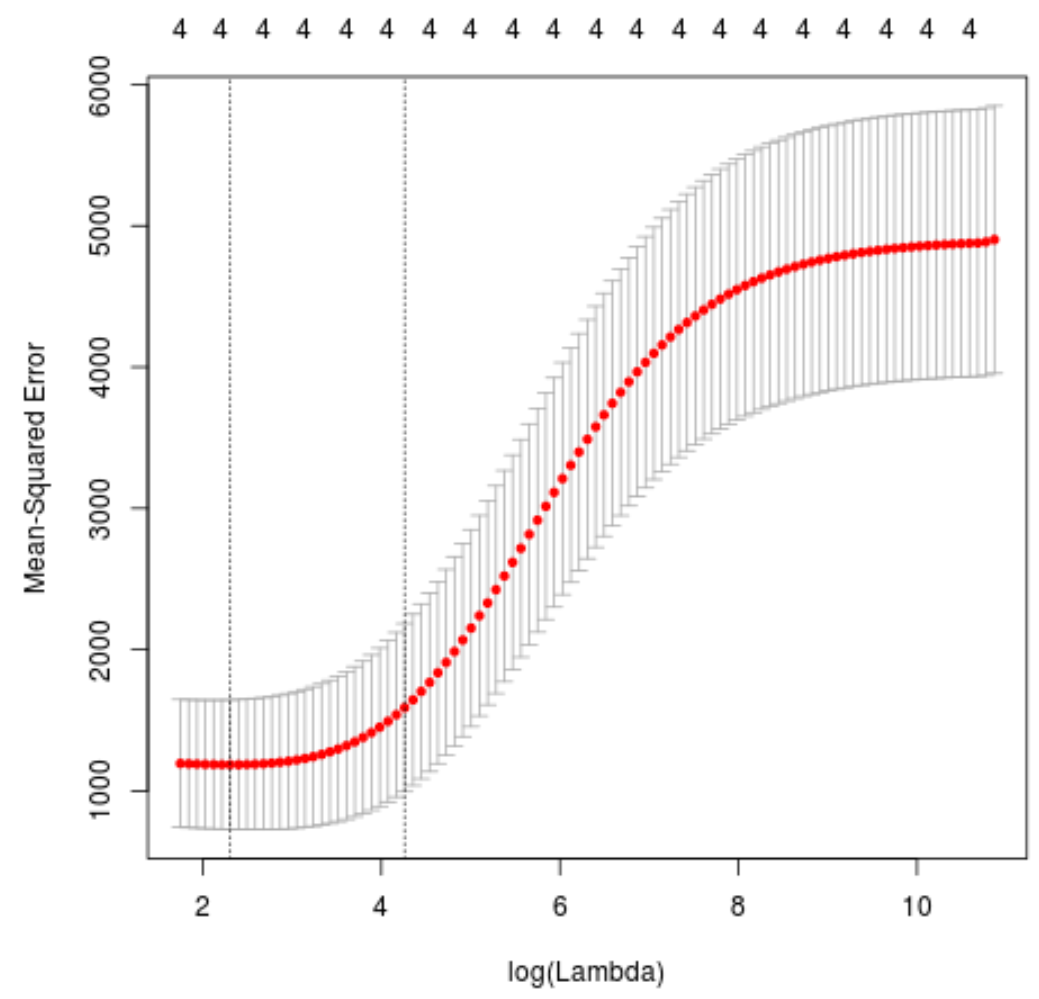
De lambdawaarde die de MSE-test minimaliseert blijkt 10,04567 te zijn.

Stap 4: Analyseer het uiteindelijke model

Ten slotte kunnen we het uiteindelijke model analyseren dat wordt geproduceerd door de optimale lambdawaarde.

We kunnen de volgende code gebruiken om de coëfficiëntschattingen voor dit model te verkrijgen:

 #find coefficients of best model
best_model <- glmnet(x, y, alpha = 0 , lambda = best_lambda)
coef(best_model)

5 x 1 sparse Matrix of class "dgCMatrix"
                    s0
(Intercept) 475.242646
mpg -3.299732
wt 19.431238
drat -1.222429
qsec -17.949721

We kunnen ook een Trace-plot maken om te visualiseren hoe de schattingen van de coëfficiënten zijn veranderd als gevolg van de toename van de lambda:

 #produce Ridge trace plot
plot(model, xvar = " lambda ") 

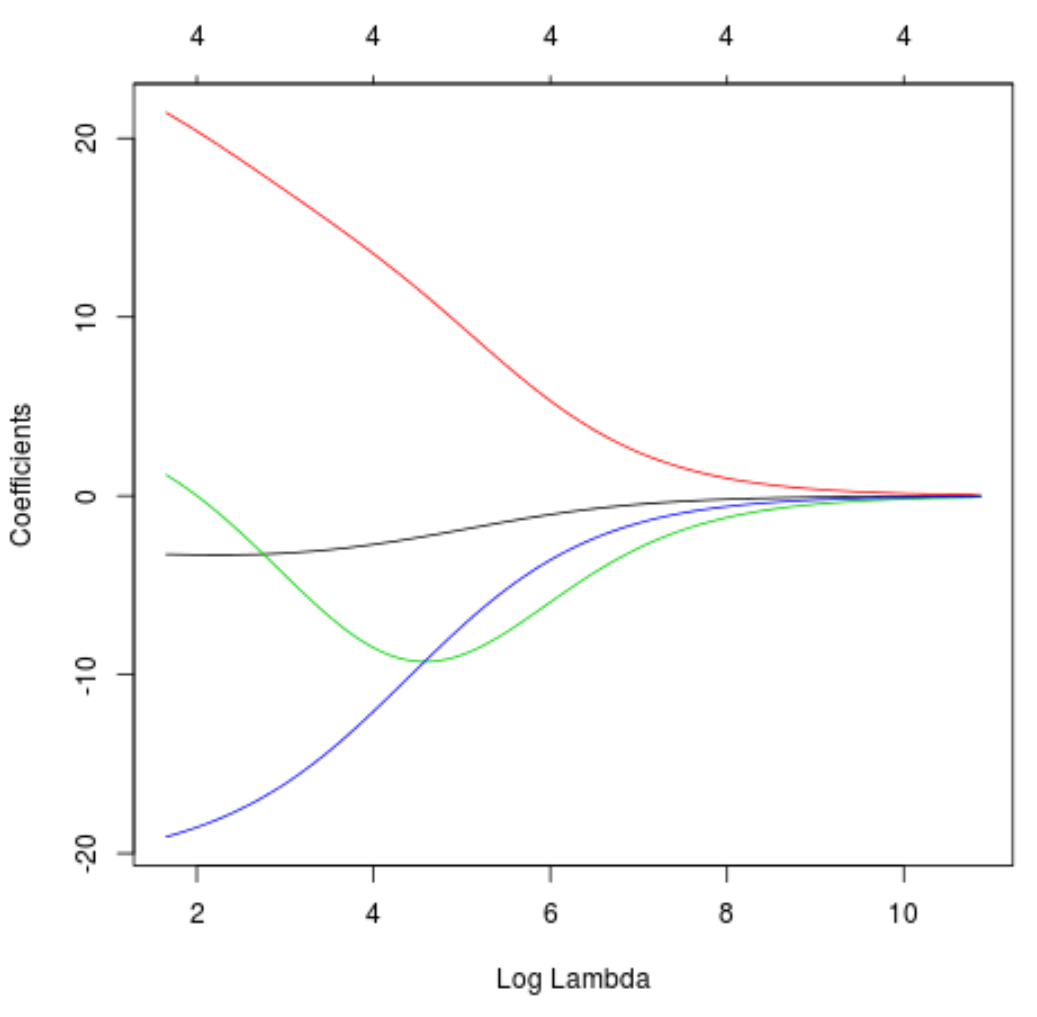
Ten slotte kunnen we de R-kwadraat van het model berekenen op basis van de trainingsgegevens:

 #use fitted best model to make predictions
y_predicted <- predict (model, s = best_lambda, newx = x)

#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)

#find R-Squared
rsq <- 1 - sse/sst
rsq

[1] 0.7999513

Het R-kwadraat blijkt 0,7999513 te zijn. Dat wil zeggen dat het beste model 79,99% van de variatie in de responswaarden van de trainingsgegevens kon verklaren.

De volledige R-code die in dit voorbeeld wordt gebruikt, vindt u hier .