Wat is een bland-altman-plot? (definitie & #038; voorbeeld)

Een Bland-Altman-plot wordt gebruikt om meetverschillen tussen twee verschillende instrumenten of twee verschillende meettechnieken te visualiseren.

Het wordt vaak gebruikt om de gelijkenis van een nieuw instrument of een nieuwe techniek om iets te meten te evalueren met het instrument of de techniek die momenteel in gebruik is.

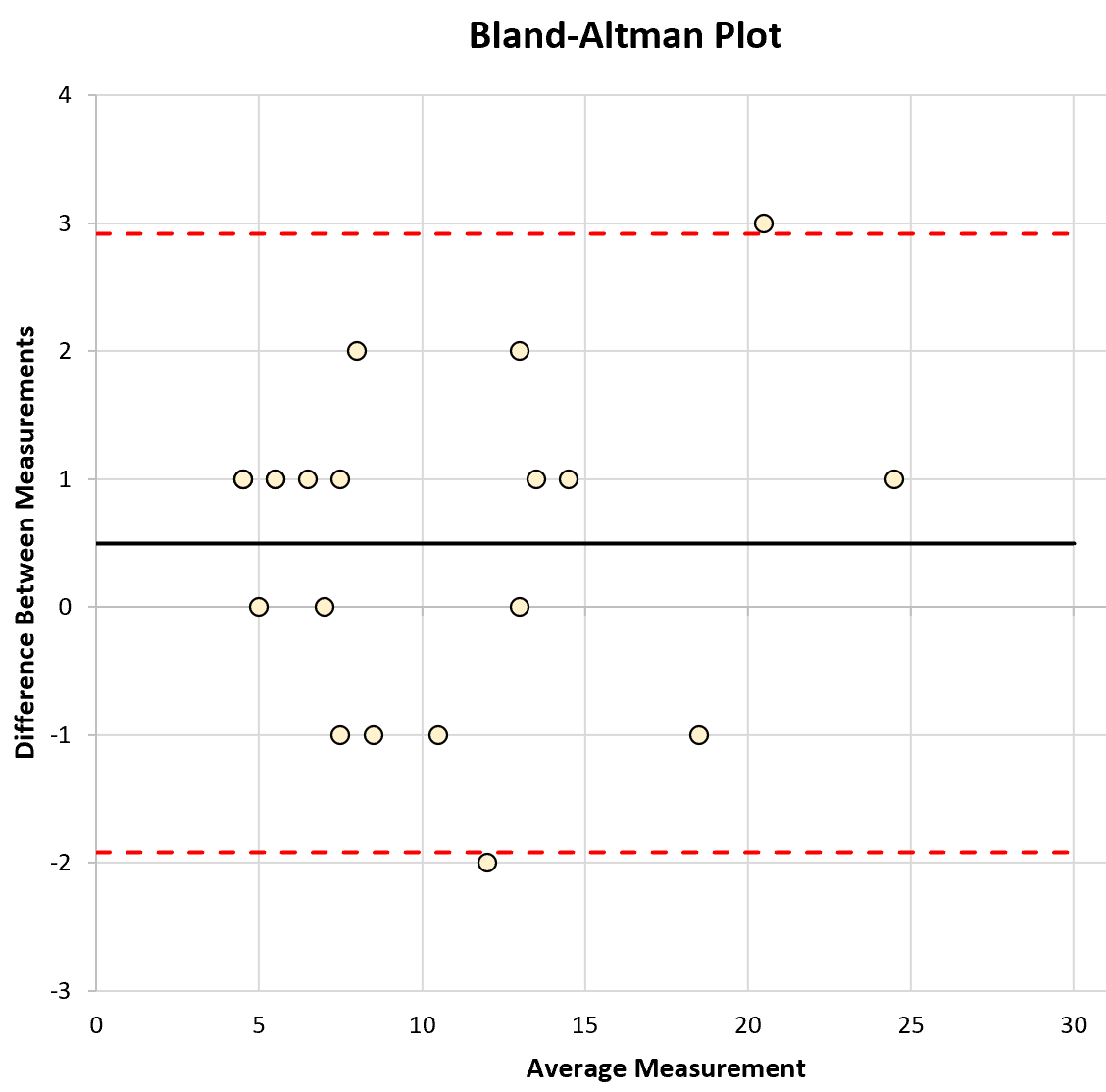
De x-as van de grafiek geeft de gemiddelde meting van de twee instrumenten weer en de y-as geeft het verschil in metingen tussen de twee instrumenten weer.

De volgende drie regels worden ook weergegeven in de plot:

• Het gemiddelde verschil in metingen tussen de twee instrumenten
• De bovengrens van het 95%-betrouwbaarheidsinterval voor het gemiddelde verschil
• De ondergrens van het 95%-betrouwbaarheidsinterval voor het gemiddelde verschil

Dit type plot is handig om twee dingen te bepalen:

1. Wat is het gemiddelde verschil in metingen tussen de twee instrumenten?

De horizontale lijn in het midden van de grafiek toont het gemiddelde verschil in metingen tussen de twee instrumenten. Deze waarde wordt vaak ‘bias’ tussen instrumenten genoemd.

Hoe verder deze waarde van nul verwijderd is, hoe groter het gemiddelde verschil in metingen tussen instrumenten.

2. Wat is de typische mate van overeenstemming tussen de twee instrumenten?

De bovenste en onderste betrouwbaarheidsintervallijnen geven ons een idee van het typische bereik van overeenstemming tussen de twee instrumenten. Over het algemeen valt 95% van de verschillen tussen de twee instrumenten binnen deze betrouwbaarheidsgrenzen.

Hoe breder het betrouwbaarheidsinterval, hoe groter het bereik van de meetverschillen tussen de twee instrumenten.

Het volgende stapsgewijze voorbeeld laat zien hoe u een Bland-Altman-plot helemaal opnieuw kunt maken en interpreteren.

Opmerking: een Bland-Altman-plot wordt ook wel een Tukey Mean Difference-plot genoemd. Deze namen worden door elkaar gebruikt.

Stap 1: Verzamel gegevens

Stel dat een bioloog wil weten hoe vergelijkbaar twee verschillende instrumenten zijn voor het meten van het gewicht van kikkers, in grammen. Hij gebruikt twee instrumenten (A en B) om dezelfde set van twintig kikkers te wegen.

Het gewicht van de kikkers, gemeten door elk instrument, wordt weergegeven in de volgende tabel:

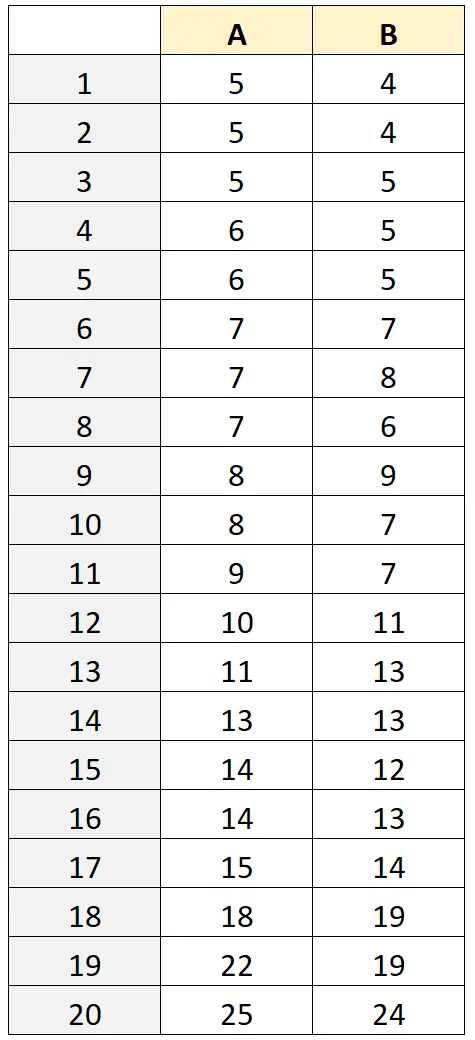
Stap 2: Bereken de gemiddelde meting en het verschil tussen de metingen

Vervolgens berekenen we de gemiddelde maat ((A+B)/2) en het verschil in maten (AB) voor elke kikker:

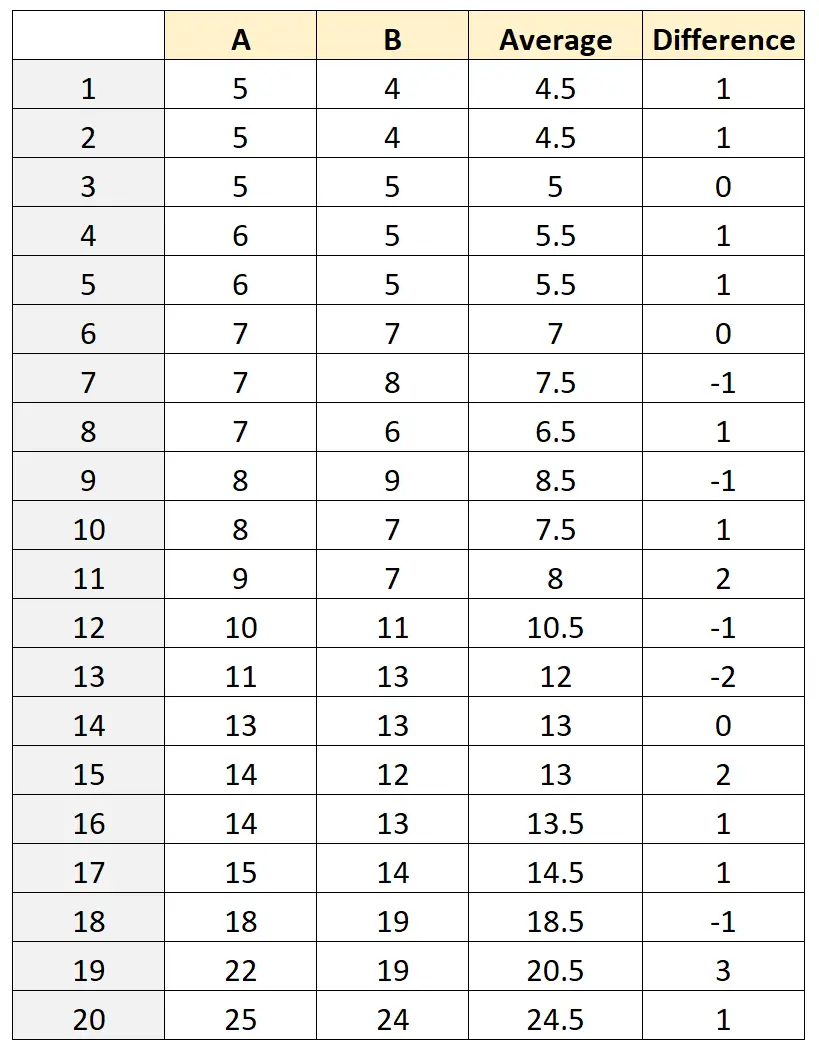
Stap 3: Bereken het gemiddelde verschil en het betrouwbaarheidsinterval

Het gemiddelde van de waarden in de kolom Verschil blijkt 0,5 te zijn.

De standaardafwijking van de waarden in de kolom Verschil blijkt 1,235 te zijn.

De boven- en ondergrenzen van het betrouwbaarheidsinterval voor het gemiddelde verschil kunnen als volgt worden berekend:

Bovengrens: x + 1,96*s = 0,5 + 1,96*1,235 = 2,92

Ondergrens: x – 1,96*s = 0,5 – 1,96*1,235 = -1,92

Zo interpreteert u deze waarden:

• Gemiddeld weegt instrument A 0,5 gram meer dan instrument B.
• 95% van de gewichtsverschillen tussen de twee instrumenten moeten tussen -1,92 gram en 2,92 gram liggen.

Vervolgens maken we een Bland-Altman-plot om deze waarden te visualiseren.

Stap 4: Maak de plot

Vervolgens kunnen we de volgende grafiek maken die de gemiddelde meting van de twee instrumenten op de x-as en het verschil tussen de metingen op de y-as toont.

We kunnen ook een horizontale lijn toevoegen aan het gemiddelde verschil tussen metingen (0,5), evenals een bovenste betrouwbaarheidsgrens (2,92) en een onderste betrouwbaarheidsgrens (-1,92) die we bij de vorige stap hebben berekend:

Aanvullende bronnen

Hoe u een Bland-Altman-plot in Excel maakt
Hoe maak je een Bland-Altman-plot in R
Hoe u een Bland-Altman-plot in Python maakt