Een roc-curve tekenen in python (stap voor stap)

Logistische regressie is een statistische methode die we gebruiken om een regressiemodel te fitten wanneer de responsvariabele binair is. Om te evalueren hoe goed een logistisch regressiemodel bij een dataset past, kunnen we naar de volgende twee statistieken kijken:

• Gevoeligheid: waarschijnlijkheid dat het model een positief resultaat voorspelt voor een waarneming terwijl het resultaat daadwerkelijk positief is. Dit wordt ook wel het “echte positieve percentage” genoemd.
• Specificiteit: de kans dat het model een negatief resultaat voorspelt voor een waarneming terwijl het resultaat feitelijk negatief is. Dit wordt ook wel het ‘echte negatieve tarief’ genoemd.

Eén manier om deze twee metingen te visualiseren is door een ROC-curve te maken, wat staat voor ‘receiver operating karakteristieke’-curve. Dit is een grafiek die de gevoeligheid en specificiteit van een logistisch regressiemodel weergeeft.

Het volgende stapsgewijze voorbeeld laat zien hoe u een ROC-curve in Python kunt maken en interpreteren.

Stap 1: Importeer de benodigde pakketten

Eerst zullen we de benodigde pakketten importeren om logistieke regressie in Python uit te voeren:

 import pandas as pd
import numpy as np
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn import metrics
import matplotlib. pyplot as plt

Stap 2: Pas het logistische regressiemodel aan

Vervolgens importeren we een dataset en passen we er een logistisch regressiemodel aan toe:

 #import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)

#define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0) 

#instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression. fit (X_train,y_train)

Stap 3: Teken de ROC-curve

Vervolgens berekenen we het werkelijk positieve percentage en het fout-positieve percentage en creëren we een ROC-curve met behulp van het Matplotlib-datavisualisatiepakket:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr)
plt. ylabel (' True Positive Rate ')
plt. xlabel (' False Positive Rate ')
plt. show () 

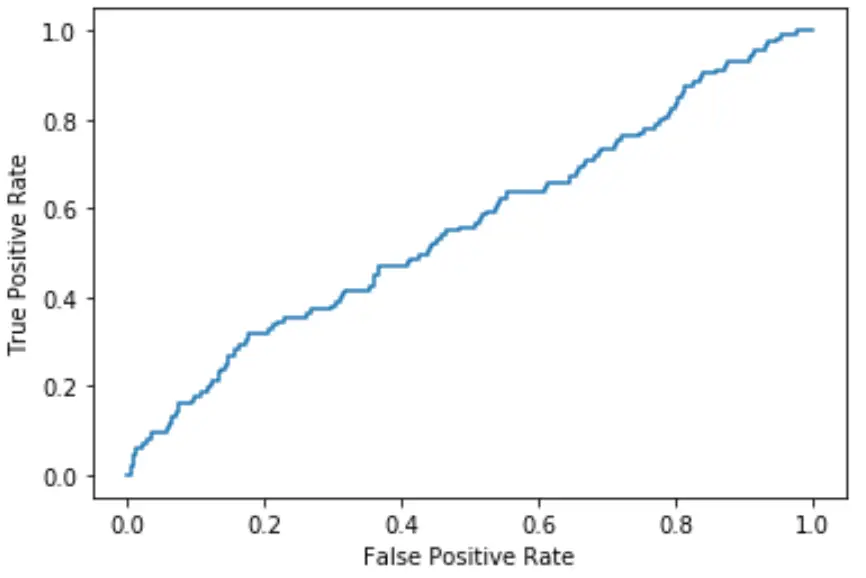
Hoe dichter de curve bij de linkerbovenhoek van de grafiek past, hoe beter het model de gegevens in categorieën kan indelen.

Zoals we uit de bovenstaande grafiek kunnen zien, slaagt dit logistische regressiemodel er behoorlijk slecht in om de gegevens in categorieën te sorteren.

Om dit te kwantificeren kunnen we de AUC (gebied onder de curve) berekenen, die ons vertelt hoeveel van de grafiek zich onder de curve bevindt.

Hoe dichter de AUC bij 1 ligt, hoe beter het model. Een model met een AUC gelijk aan 0,5 is niet beter dan een model dat willekeurige classificaties uitvoert.

Stap 4: Bereken de AUC

We kunnen de volgende code gebruiken om de AUC van het model te berekenen en deze in de rechter benedenhoek van de ROC-plot weer te geven:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. ylabel (' True Positive Rate ')
plt. xlabel (' False Positive Rate ')
plt. legend (loc=4)
plt. show () 

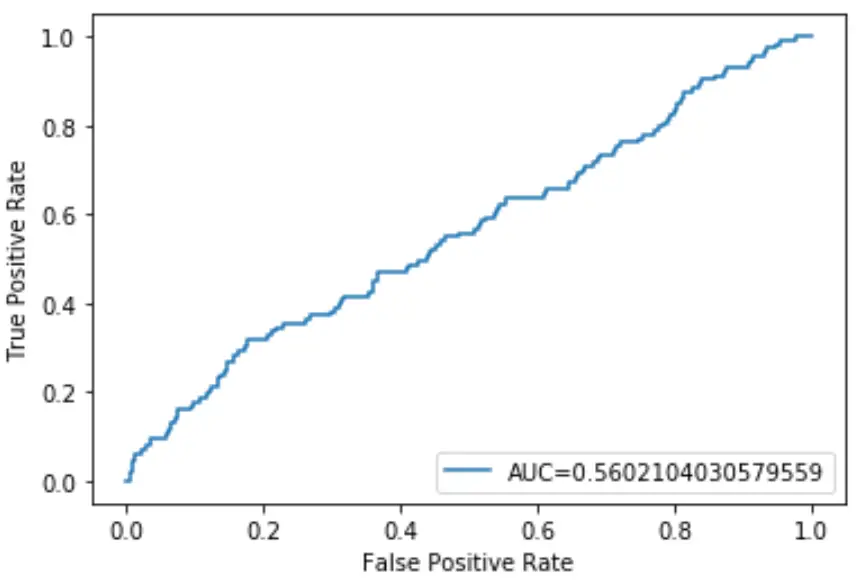
De AUC van dit logistieke regressiemodel blijkt 0,5602 te zijn. Aangezien dit cijfer gesloten is tot 0,5, bevestigt dit dat het model de gegevens slecht classificeert.

Gerelateerd: Hoe meerdere ROC-curven in Python te plotten