Gegevens transformeren in r (logboek, vierkantswortel, kubuswortel)

Veel statistische tests gaan ervan uit dat de residuen van een responsvariabele normaal verdeeld zijn.

De residuen zijn echter vaak niet normaal verdeeld. Eén manier om dit probleem op te lossen is door de responsvariabele te transformeren met behulp van een van de volgende drie transformaties:

1. Logtransformatie: transformeer de responsvariabele van y naar log(y) .

2. Vierkantsworteltransformatie: Transformeer de responsvariabele van y naar √y .

3. Derdemachtsworteltransformatie: transformeer de responsvariabele van y naar y ^1/3 .

Door deze transformaties uit te voeren, benadert de responsvariabele doorgaans de normale verdeling. De volgende voorbeelden laten zien hoe u deze transformaties in R kunt uitvoeren.

Logtransformatie in R

De volgende code laat zien hoe u een logtransformatie uitvoert op een antwoordvariabele:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform log transformation
log_y <- log10(df$y)

De volgende code laat zien hoe u histogrammen maakt om de verdeling van y weer te geven voor en na het uitvoeren van een logtransformatie:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for log-transformed distribution 
hist(log_y, col='coral2', main='Log Transformed')

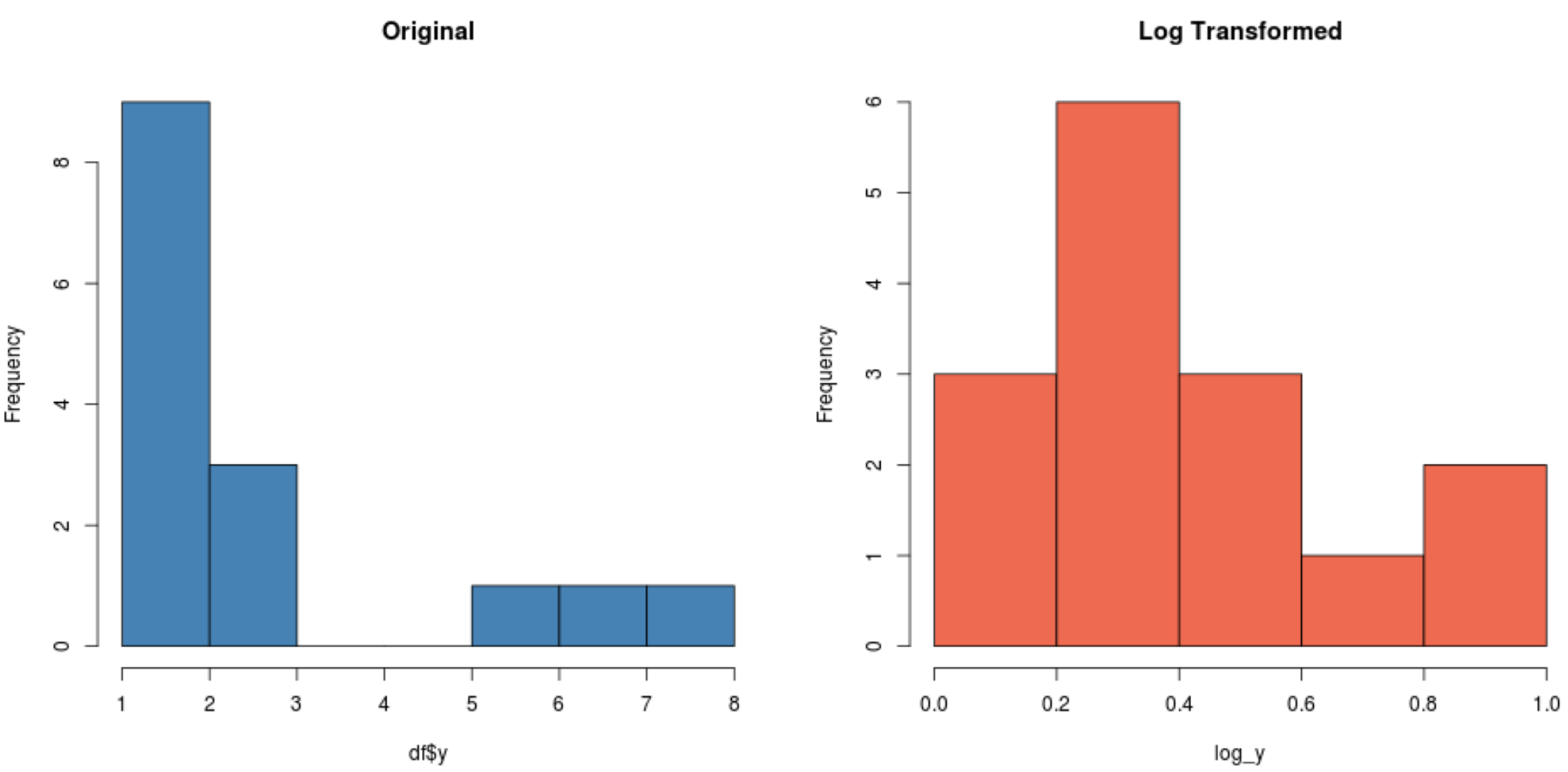
Merk op dat de log-getransformeerde distributie veel normaler is dan de oorspronkelijke distributie. Het is nog steeds geen perfecte „klokvorm“, maar het ligt dichter bij een normale verdeling dan de oorspronkelijke verdeling.

Als we op elke verdeling een Shapiro-Wilk-test uitvoeren, zullen we ontdekken dat de oorspronkelijke verdeling niet voldoet aan de normaliteitsaanname, terwijl de log-getransformeerde verdeling dat niet doet (bij α = 0,05):

 #perform Shapiro-Wilk Test on original data
shapiro.test(df$y)

	Shapiro-Wilk normality test

data: df$y
W = 0.77225, p-value = 0.001655

#perform Shapiro-Wilk Test on log-transformed data 
shapiro.test(log_y)

	Shapiro-Wilk normality test

data:log_y
W = 0.89089, p-value = 0.06917

Vierkantsworteltransformatie in R

De volgende code laat zien hoe u een vierkantsworteltransformatie uitvoert op een antwoordvariabele:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
sqrt_y <- sqrt(df$y)

De volgende code laat zien hoe u histogrammen maakt om de verdeling van y weer te geven voor en na het uitvoeren van een worteltransformatie:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(sqrt_y, col='coral2', main='Square Root Transformed') 

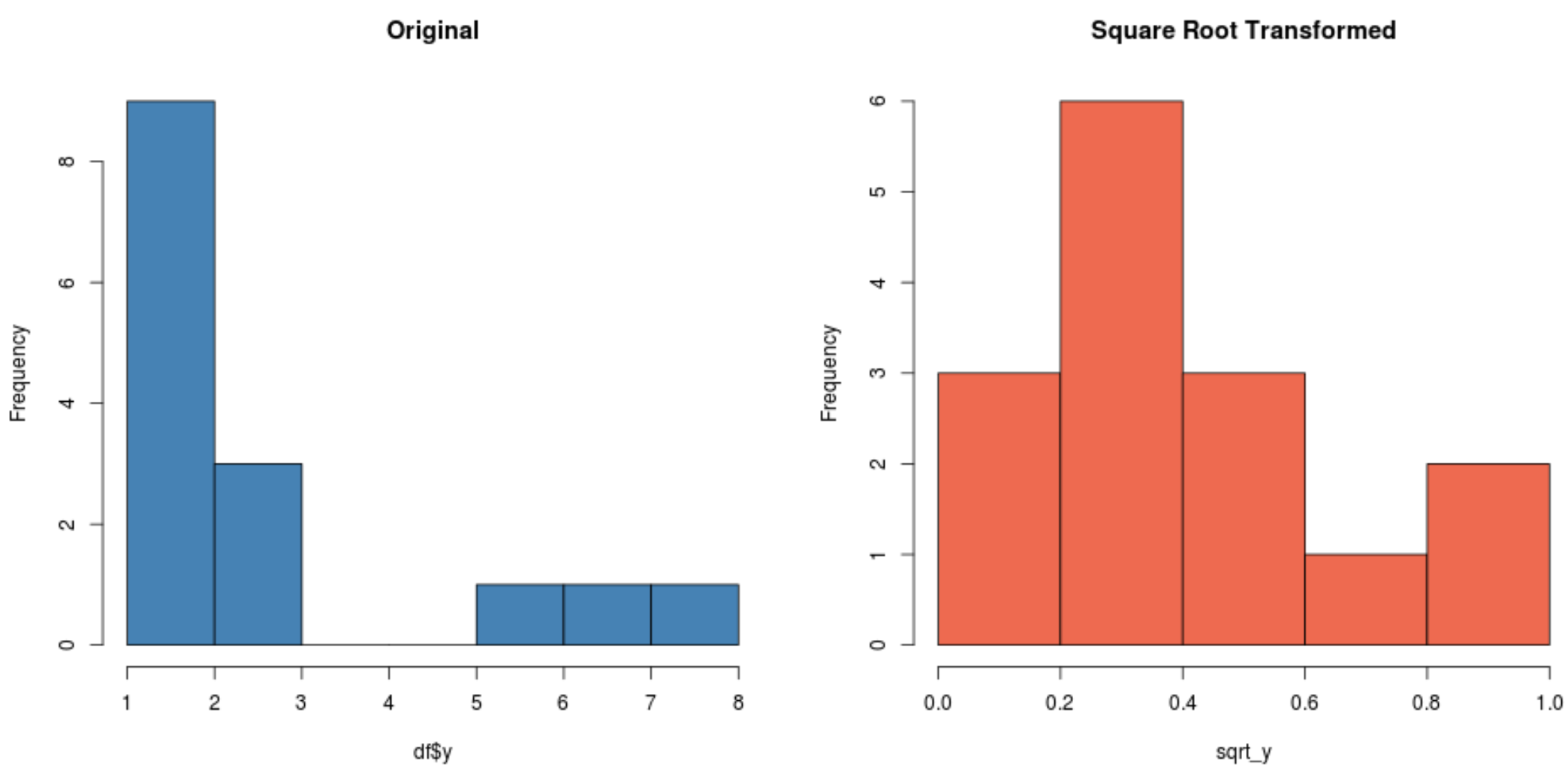
Merk op dat de getransformeerde vierkantswortelverdeling veel normaler verdeeld is dan de oorspronkelijke verdeling.

Derdemachtsworteltransformatie in R

De volgende code laat zien hoe u een derdemachtsworteltransformatie uitvoert op een antwoordvariabele:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
cube_y <- df$y^(1/3)

De volgende code laat zien hoe u histogrammen maakt om de verdeling van y weer te geven voor en na het uitvoeren van een worteltransformatie:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(cube_y, col='coral2', main='Cube Root Transformed') 

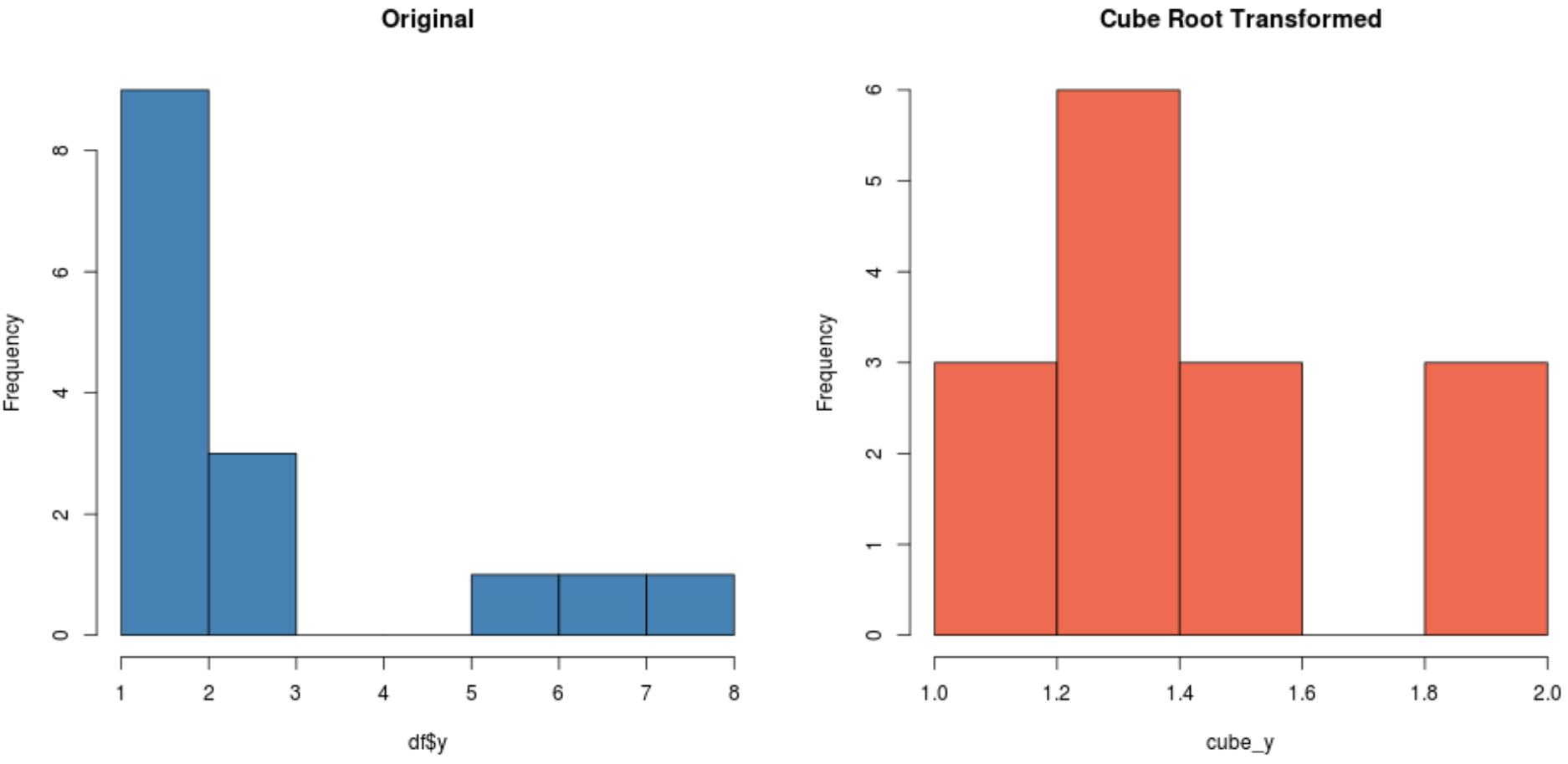
Afhankelijk van uw dataset kan een van deze transformaties een nieuwe dataset opleveren die normaler verdeeld is dan de andere.