Gegevens onttrenden: met voorbeelden

Tijdreeksgegevens ‘detrending’ betekent het verwijderen van een onderliggende trend in de gegevens. De belangrijkste reden dat we dit willen doen is om onderliggende trends gemakkelijker te visualiseren in gegevens die seizoensgebonden of cyclisch zijn.

Neem bijvoorbeeld de volgende tijdreeksgegevens die de totale omzet van een bedrijf gedurende twintig opeenvolgende perioden vertegenwoordigen:

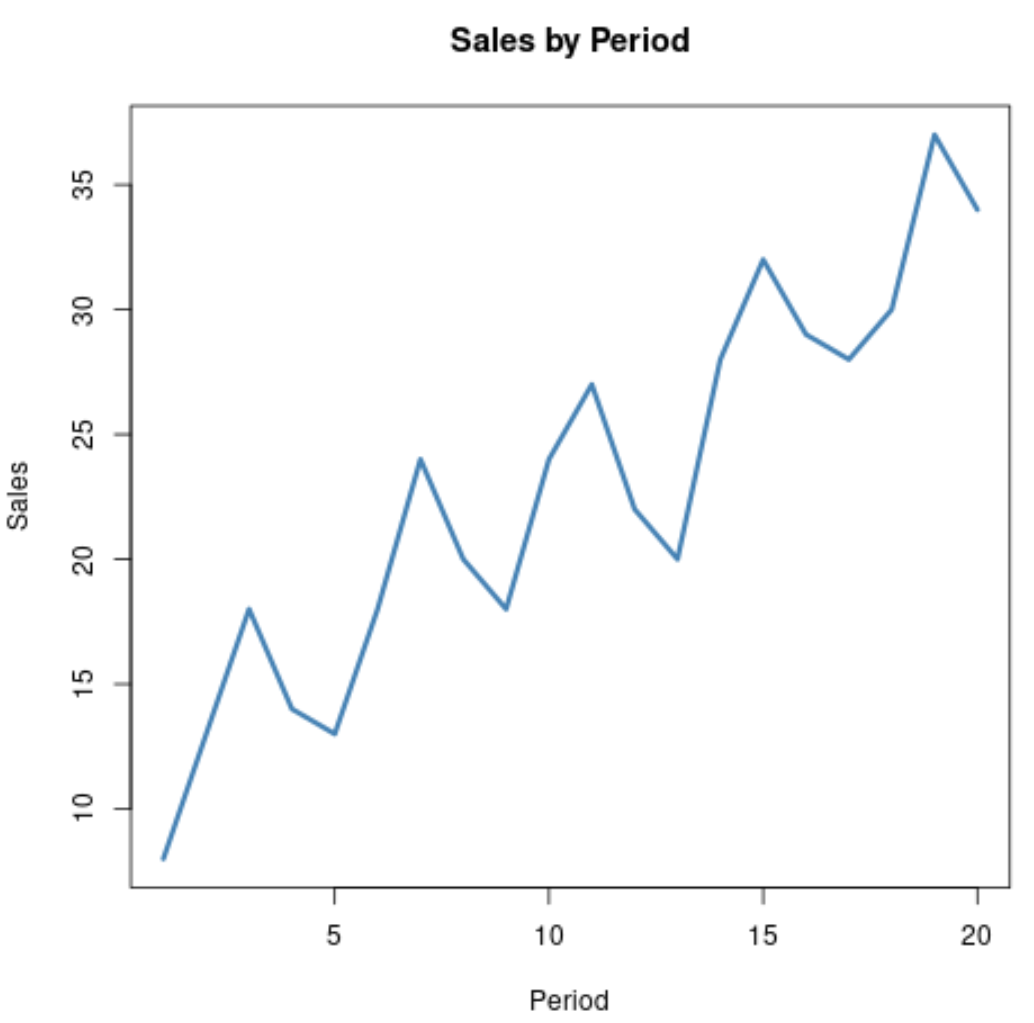
Het is duidelijk dat de verkopen in de loop van de tijd de neiging hebben te stijgen, maar er lijkt ook een cyclische of seizoenstrend in de gegevens te zitten, zoals blijkt uit de kleine ‘heuveltjes’ die zich in de loop van de tijd voordoen.

Om een beter zicht te krijgen op deze cyclische trend kunnen we de gegevens laten leeglopen. In dit geval zou dit betekenen dat de algehele opwaartse trend in de loop van de tijd wordt verwijderd, zodat de resulterende gegevens alleen de cyclische trend weergeven.

Er zijn twee veelgebruikte methoden om tijdreeksgegevens leeg te laten lopen:

1. Tendens door differentiatie

2. Degradatie door modelaanpassing

Deze tutorial geeft een korte uitleg van elke methode.

Methode 1: Ontspanning door differentiatie

Eén manier om tijdreeksgegevens te verminderen is door eenvoudigweg een nieuwe gegevensset te maken waarin elke waarneming het verschil vertegenwoordigt tussen zichzelf en de vorige waarneming.

De volgende afbeelding laat bijvoorbeeld zien hoe u differentiëren kunt gebruiken om een gegevensreeks te detrenderen.

Om de eerste waarde van de gedetrendeerde tijdreeksgegevens te verkrijgen, berekenen we 13 – 8 = 5. Om vervolgens de volgende waarde te krijgen, berekenen we 18-13 = 5, enzovoort.

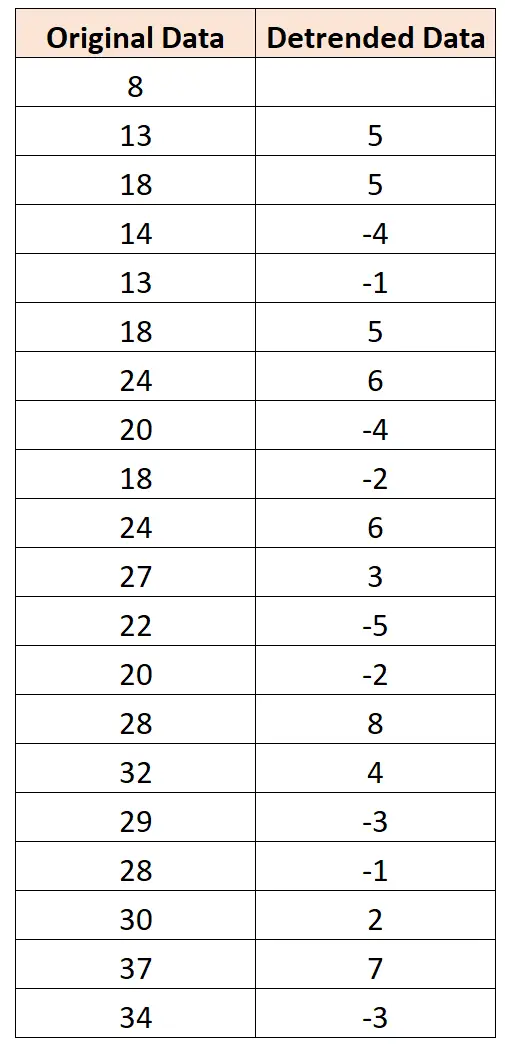
Het volgende diagram toont de oorspronkelijke tijdreeksgegevens:

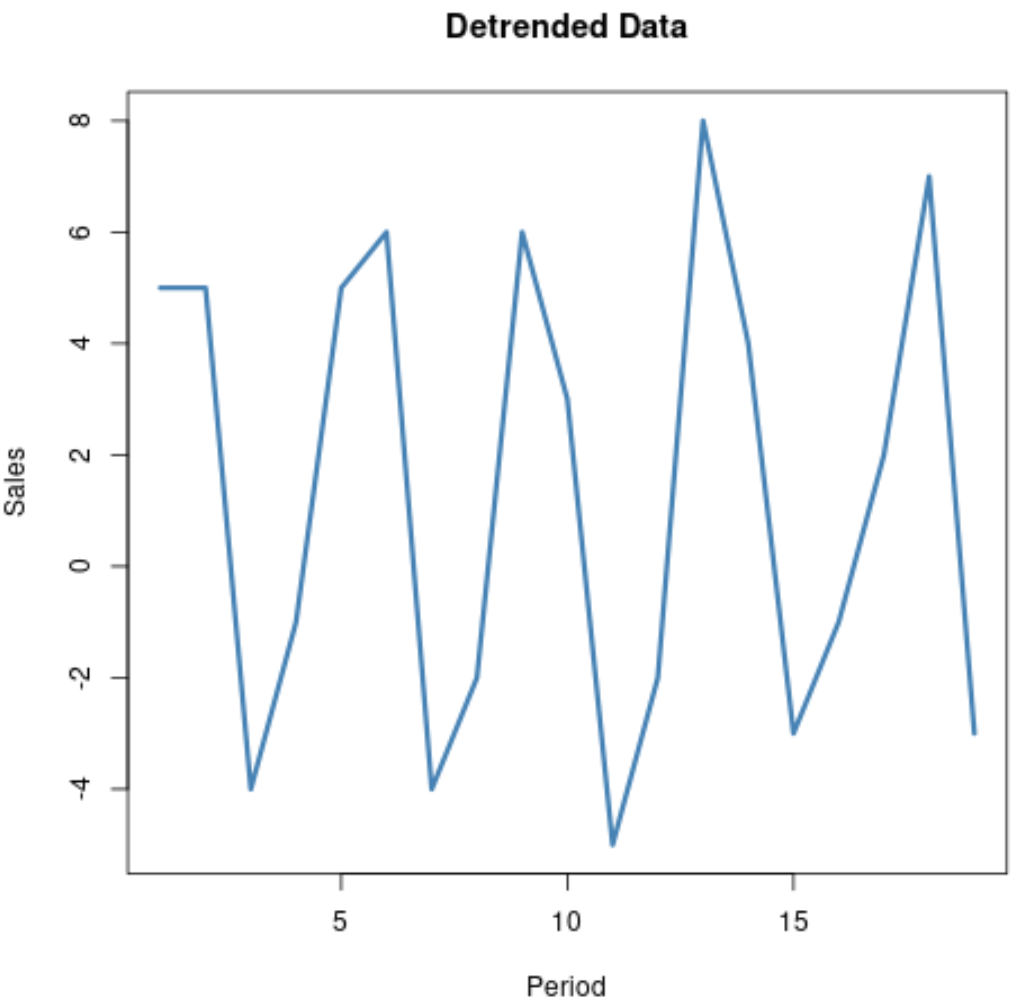
En deze grafiek toont de gegevens zonder trend:

Merk op hoeveel gemakkelijker het is om de seizoenstrend in de tijdreeksgegevens in deze grafiek te zien, omdat de algehele opwaartse trend is verwijderd.

Methode 2: Afbraak door modelaanpassing

Een andere manier om tijdreeksgegevens te onttrenden is door een regressiemodel aan de gegevens te koppelen en vervolgens het verschil te berekenen tussen de waargenomen waarden en de voorspelde waarden van het model.

Stel dat we dezelfde dataset hebben:

Als we een eenvoudig lineair regressiemodel op de gegevens passen, kunnen we voor elke waarneming in de dataset een voorspelde waarde verkrijgen.

We kunnen dan voor elke waarneming het verschil vinden tussen de werkelijke waarde en de voorspelde waarde. Deze verschillen vertegenwoordigen gedetrendeerde gegevens.

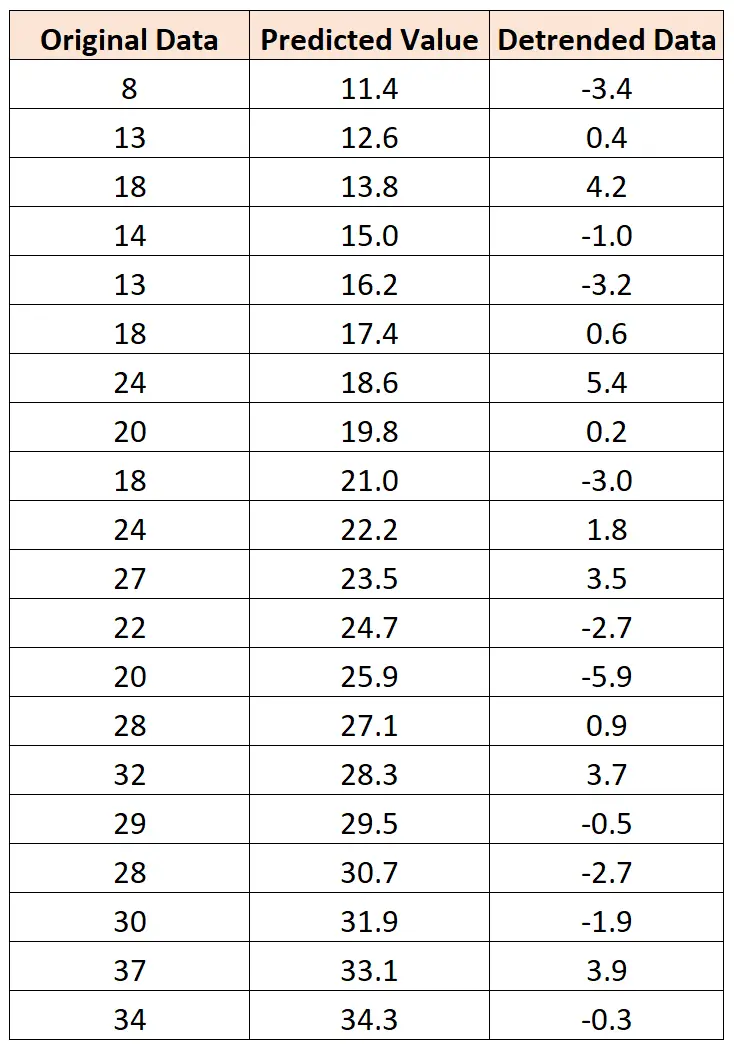
Als we een grafiek van de gegevens maken zonder trend, kunnen we de seizoens- of cyclische trend van de gegevens veel gemakkelijker visualiseren:

Merk op dat we in dit voorbeeld lineaire regressie hebben gebruikt, maar het is mogelijk om een complexere methode zoals exponentiële regressie te gebruiken als er meer een exponentiële opwaartse of neerwaartse trend in de gegevens zit.