Hoe u een tukey-kramer post hoc-test uitvoert in excel

Een eenrichtings-ANOVA wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.

De aannames die bij een ANOVA worden gebruikt, zijn als volgt:

De nulhypothese (H ₀ ): µ ₁ = µ ₂ = µ ₃ = … = µ _k (de gemiddelden zijn voor elke groep gelijk)

De alternatieve hypothese: (Ha): minstens één van de middelen verschilt van de andere

Als de p-waarde van de ANOVA onder het significantieniveau ligt, kunnen we de nulhypothese verwerpen en concluderen dat we voldoende bewijs hebben om te zeggen dat ten minste één van de groepsgemiddelden verschilt van de andere.

Dit vertelt ons echter niet welke groepen van elkaar verschillen. Dit vertelt ons eenvoudigweg dat niet alle groepsgemiddelden gelijk zijn. Om precies te weten welke groepen van elkaar verschillen, moeten we een post-hoctest uitvoeren.

De meest gebruikte post-hoc-test is de Tukey-Kramer-test , die het gemiddelde tussen elke paarsgewijze combinatie van groepen vergelijkt.

Het volgende voorbeeld laat zien hoe u de Tukey-Kramer-test in Excel uitvoert.

Voorbeeld: Tukey-Kramer-test in Excel

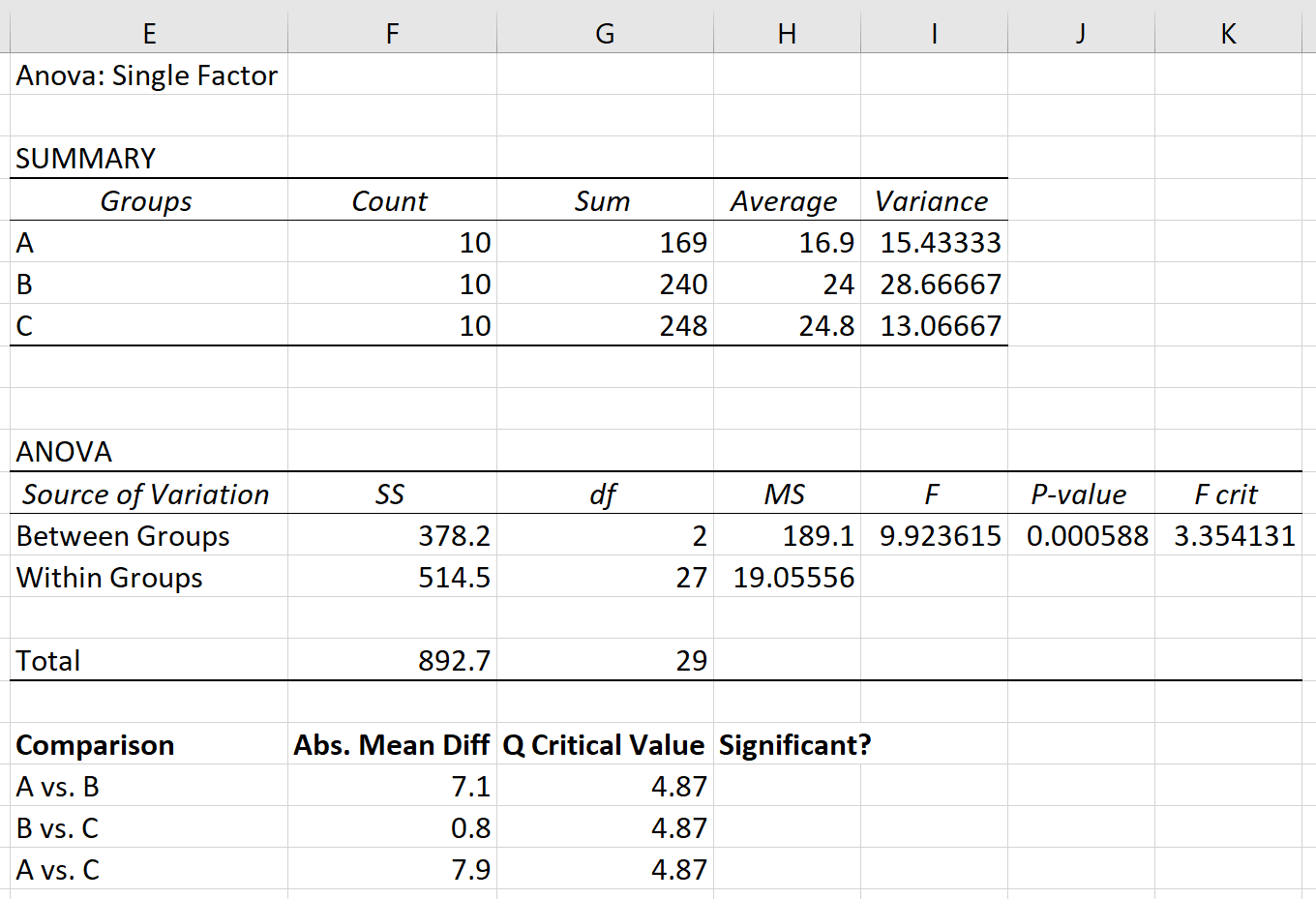
Stel dat we een eenrichtings-ANOVA uitvoeren op drie groepen: A, B en C. De resultaten van de eenrichtings-ANOVA worden hieronder weergegeven:

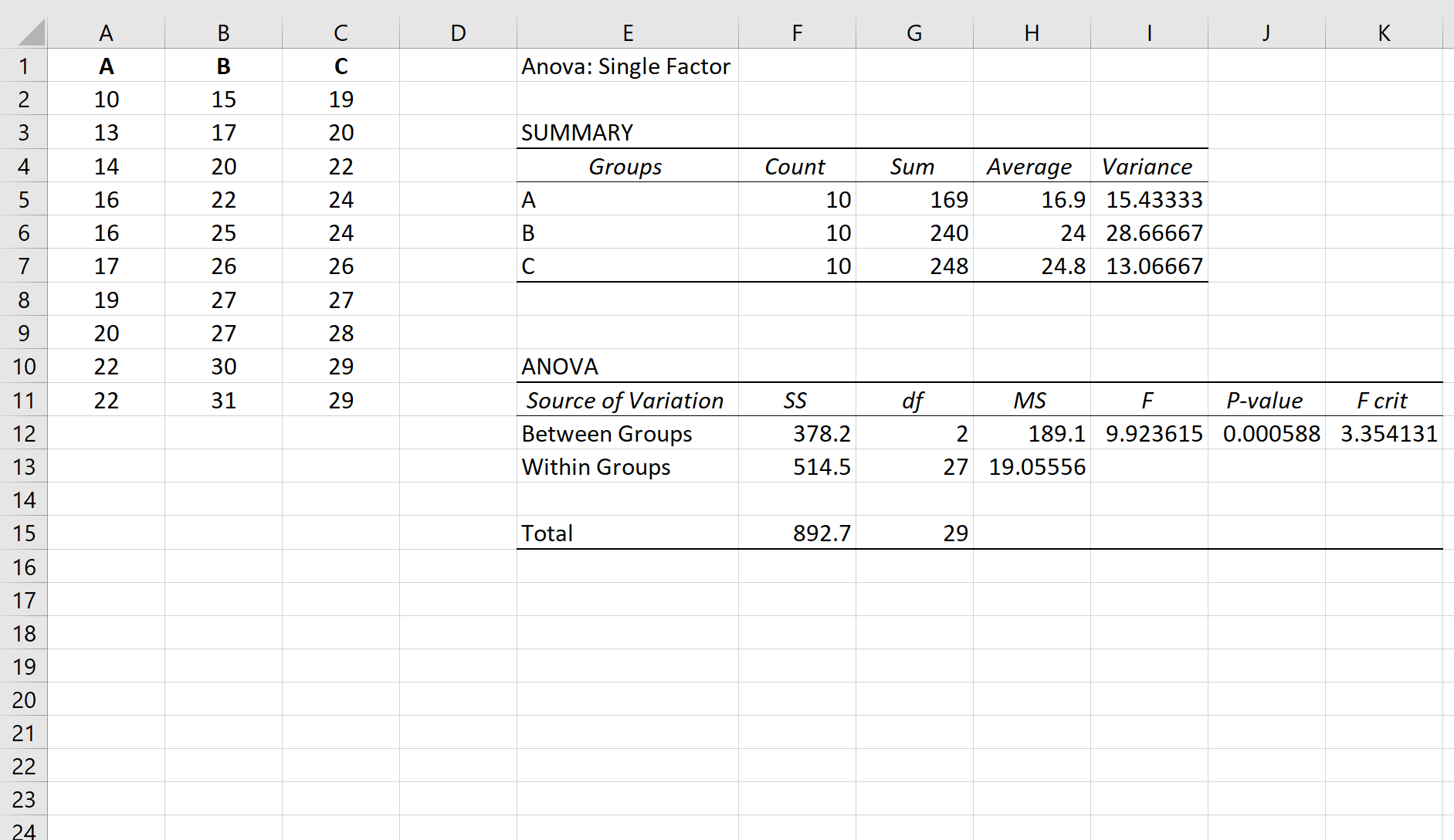
Gerelateerd: One-Way ANOVA uitvoeren in Excel

De p-waarde van de ANOVA-tabel is 0,000588 . Omdat deze p-waarde kleiner is dan 0,05, kunnen we de nulhypothese verwerpen en concluderen dat de gemiddelden tussen de drie groepen niet gelijk zijn.

Om precies te bepalen welke groepsgemiddelden verschillend zijn, kunnen we een Tukey-Kramer post hoc-test uitvoeren met behulp van de volgende stappen:

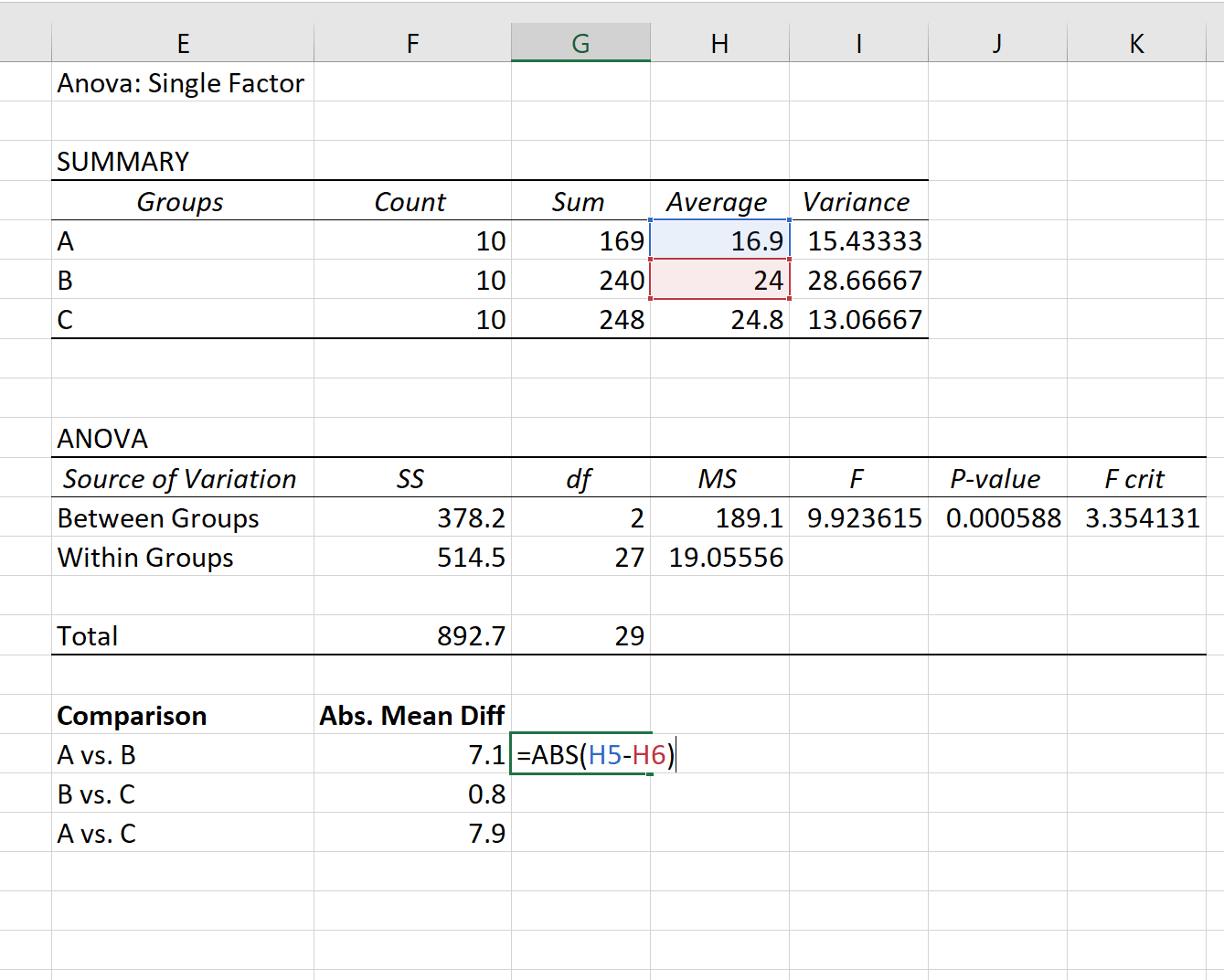
Stap 1: Zoek het absolute gemiddelde verschil tussen elke groep.

Eerst zullen we het absolute gemiddelde verschil tussen elke groep vinden met behulp van de gemiddelden in de eerste tabel van het ANOVA-resultaat:

Stap 2: Vind de kritische waarde van Q.

Vervolgens moeten we de kritische waarde van Q vinden met behulp van de volgende formule:

Kritische waarde Q = Q*√(s ² _gegroepeerd / n.)

Goud:

• Q = Waarde van het bereik van Studententabel Q
• s ² _gepoold = variantie samengevoegd over alle groepen
• niet. = Steekproefomvang voor een bepaalde groep

Om de Q-waarde te vinden, kunt u de Studentized range Q-tabel raadplegen, die er als volgt uitziet:

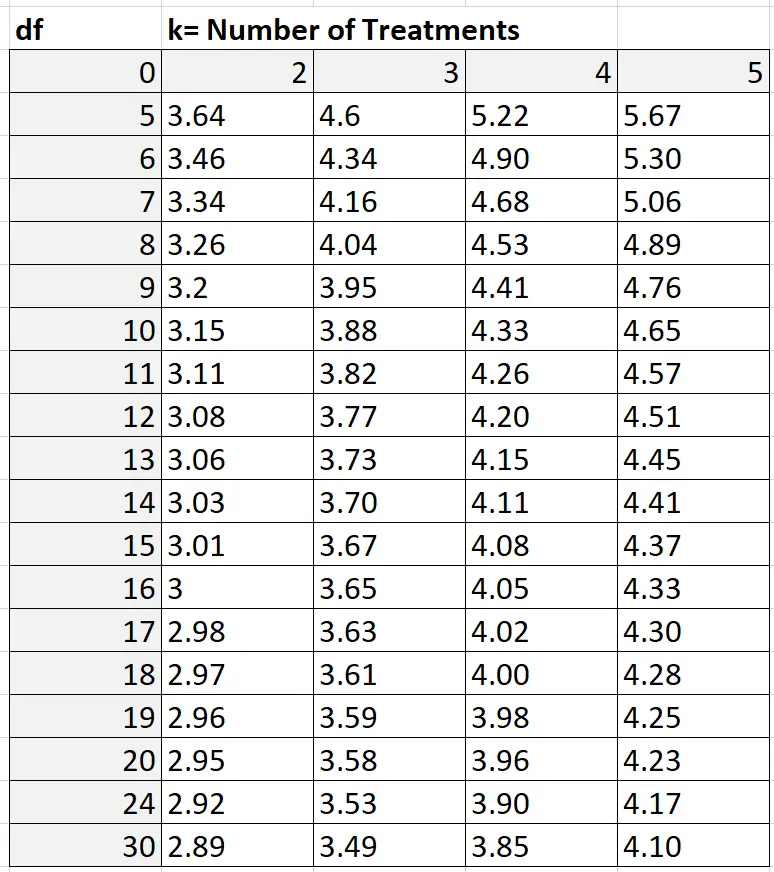
In ons voorbeeld is k = het aantal groepen, dat wil zeggen k = 3. De vrijheidsgraden worden als volgt berekend: nk = 30 – 3 = 27. Omdat 27 niet in de bovenstaande tabel staat, kunnen we een conservatieve schatting van 24 gebruiken. Gebaseerd op k = 3 en df = 24, vinden we dat Q = 3,53 .

De gepoolde variantie kan worden berekend als het gemiddelde van de varianties van de groepen, wat 19,056 blijkt te zijn.

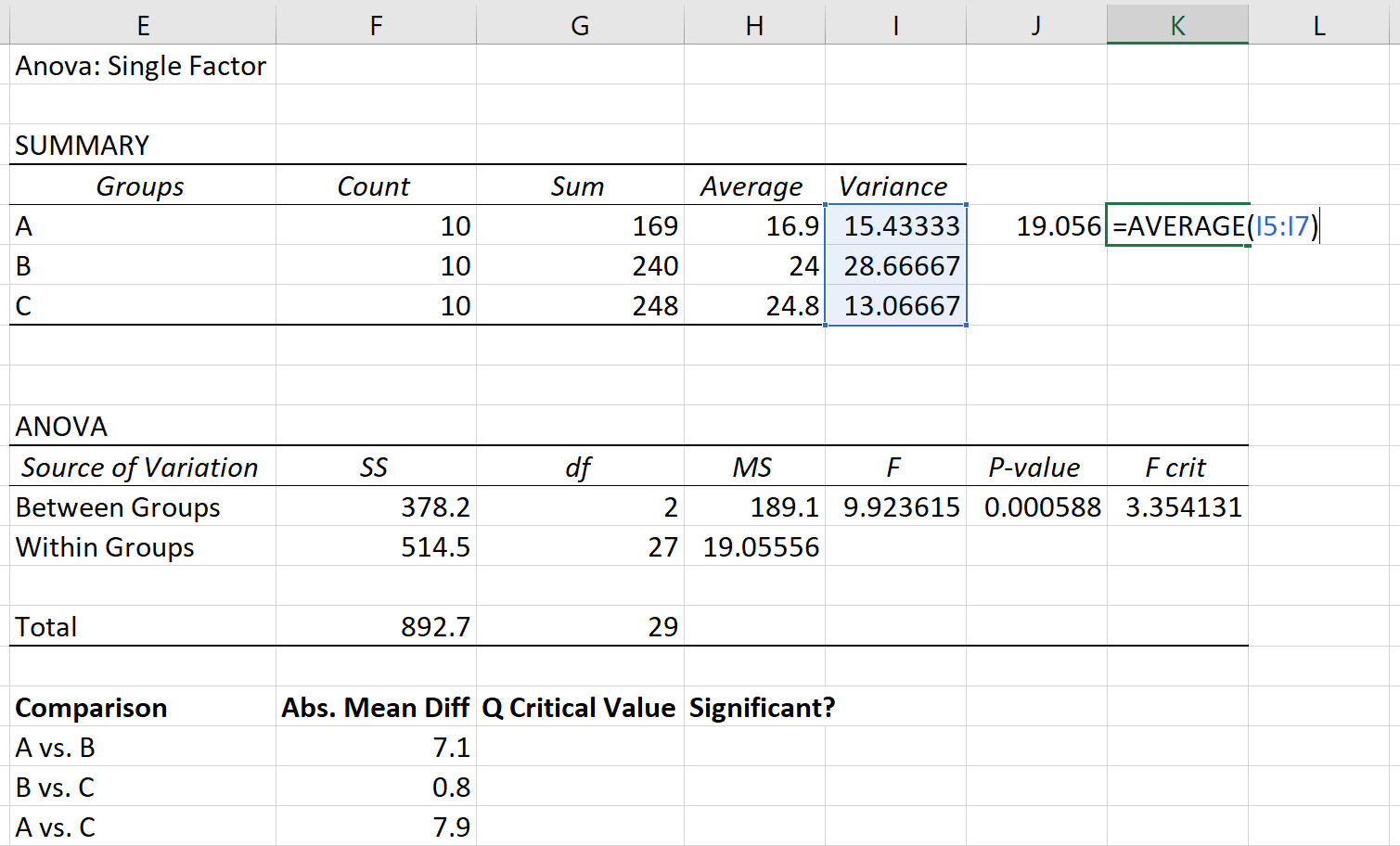
Ten slotte is de steekproefomvang van elke groep 10.

Onze kritische waarde Q kan dus als volgt worden berekend:

Kritische waarde Q = Q*√(s ² _gegroepeerd / n.) = 3,53*√(19,056/10) = 4,87 .

Stap 3: Bepaal welke groepsgemiddelden verschillend zijn .

Ten slotte kunnen we het absolute gemiddelde verschil tussen elke groep vergelijken met de kritische waarde Q. Als het absolute gemiddelde verschil groter is dan de kritische waarde Q, dan is het verschil tussen de groepsgemiddelden statistisch significant:

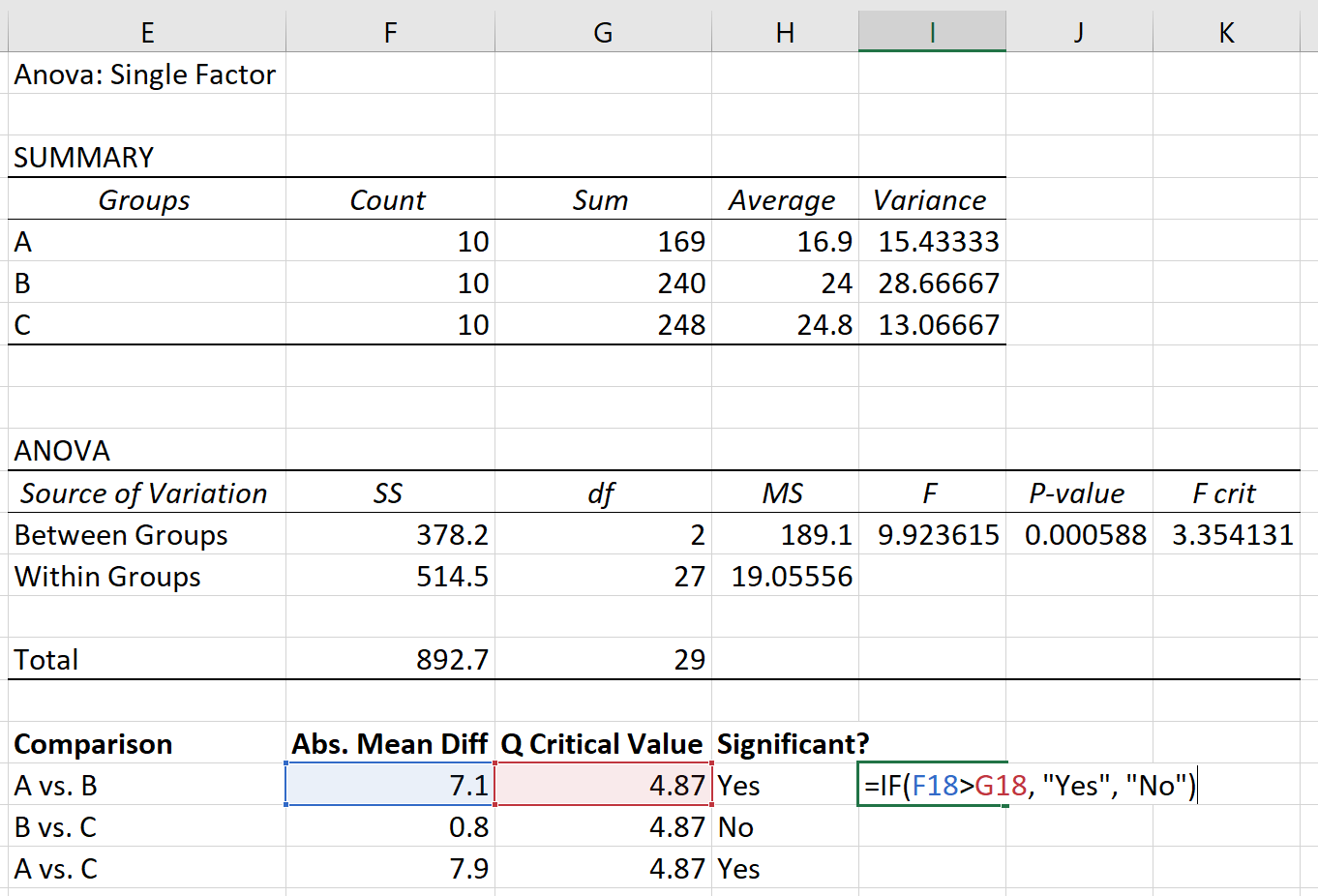
Op basis van de post-hoctest van Tukey-Kramer hebben we het volgende gevonden:

• Het verschil in gemiddelden tussen groep A en groep B is statistisch significant.
• Het verschil in gemiddelden tussen groep B en groep C is niet statistisch significant.
• Het verschil in gemiddelden tussen groep A en groep C is statistisch significant.

Aanvullende bronnen

Eenrichtings-ANOVA uitvoeren in Excel
Een handleiding voor het gebruik van post-hoctesten met ANOVA