Hoe de tukey-test uit te voeren in r

Een eenrichtings-ANOVA wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.

Als de totale p-waarde van de ANOVA-tabel onder een bepaald significantieniveau ligt, hebben we voldoende bewijs om te zeggen dat ten minste één van de groepsgemiddelden verschilt van de andere.

Dit vertelt ons echter niet welke groepen van elkaar verschillen. Dit vertelt ons eenvoudigweg dat niet alle groepsgemiddelden gelijk zijn. Om precies te weten welke groepen van elkaar verschillen, moeten we eenpost-hoctest uitvoeren.

Een van de meest gebruikte post-hoc tests is de Tukey-test , waarmee we paarsgewijze vergelijkingen kunnen maken tussen de gemiddelden van elke groep, terwijl we controleren voor het familiefoutenpercentage .

In deze tutorial wordt uitgelegd hoe u de Tukey-test uitvoert in R.

Opmerking: als een van de groepen in uw onderzoek als een controlegroep wordt beschouwd, moet u in plaats daarvan de Dunnett-test als post-hoc-test gebruiken.

Voorbeeld: Tukey-test in R

Stap 1: Monteer het ANOVA-model.

De volgende code laat zien hoe u een nep-dataset met drie groepen (A, B en C) kunt maken en een eenrichtings-ANOVA-model op de gegevens kunt passen om te bepalen of de gemiddelde waarden van elke groep gelijk zijn:

 #make this example reproducible
set.seed(0)

#create data
data <- data.frame(group = rep (c("A", "B", "C"), each = 30),
                   values = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#view first six rows of data
head(data)

  group values
1 A 2.6900916
2 A 0.7965260
3 A 1.1163717
4 A 1.7185601
5 A 2.7246234
6 A 0.6050458

#fit one-way ANOVA model
model <- aov (values~group, data=data)

#view the model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)    
group 2 98.93 49.46 30.83 7.55e-11 ***
Residuals 87 139.57 1.60                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

We kunnen zien dat de totale p-waarde uit de ANOVA-tabel 7,55e-11 is. Omdat dit getal kleiner is dan 0,05, hebben we voldoende bewijs om te zeggen dat de gemiddelde waarden in elke groep niet gelijk zijn. We kunnen dus de Tukey-test uitvoeren om precies te bepalen welke groepsgemiddelden verschillend zijn.

Stap 2: Voer de Tukey-test uit.

De volgende code laat zien hoe u de functie TukeyHSD() gebruikt om de Tukey-test uit te voeren:

 #perform Tukey's Test
TukeyHSD(model, conf.level= .95 ) 

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = values ~ group, data = data)

$group
         diff lwr upr p adj
BA 0.9777414 0.1979466 1.757536 0.0100545
CA 2.5454024 1.7656076 3.325197 0.0000000
CB 1.5676610 0.7878662 2.347456 0.0000199

De p-waarde geeft aan of er al dan niet een statistisch significant verschil bestaat tussen elk programma. De resultaten laten zien dat er een statistisch significant verschil is tussen het gemiddelde gewichtsverlies van elk programma op het significantieniveau van 0,05.

Speciaal:

• P-waarde voor het verschil in gemiddelden tussen B en A: 0,0100545
• P-waarde voor het verschil in gemiddelden tussen C en A: 0,0000000
• P-waarde voor het verschil in gemiddelden tussen C en B: 0,0000199

Stap 3: Visualiseer de resultaten.

We kunnen ook de functie plot(TukeyHSD()) gebruiken om betrouwbaarheidsintervallen te visualiseren:

 #plot confidence intervals
plot(TukeyHSD(model, conf.level= .95 ), las = 2 )

Opmerking: het las- argument geeft aan dat de vinklabels loodrecht (las=2) op de as moeten staan.

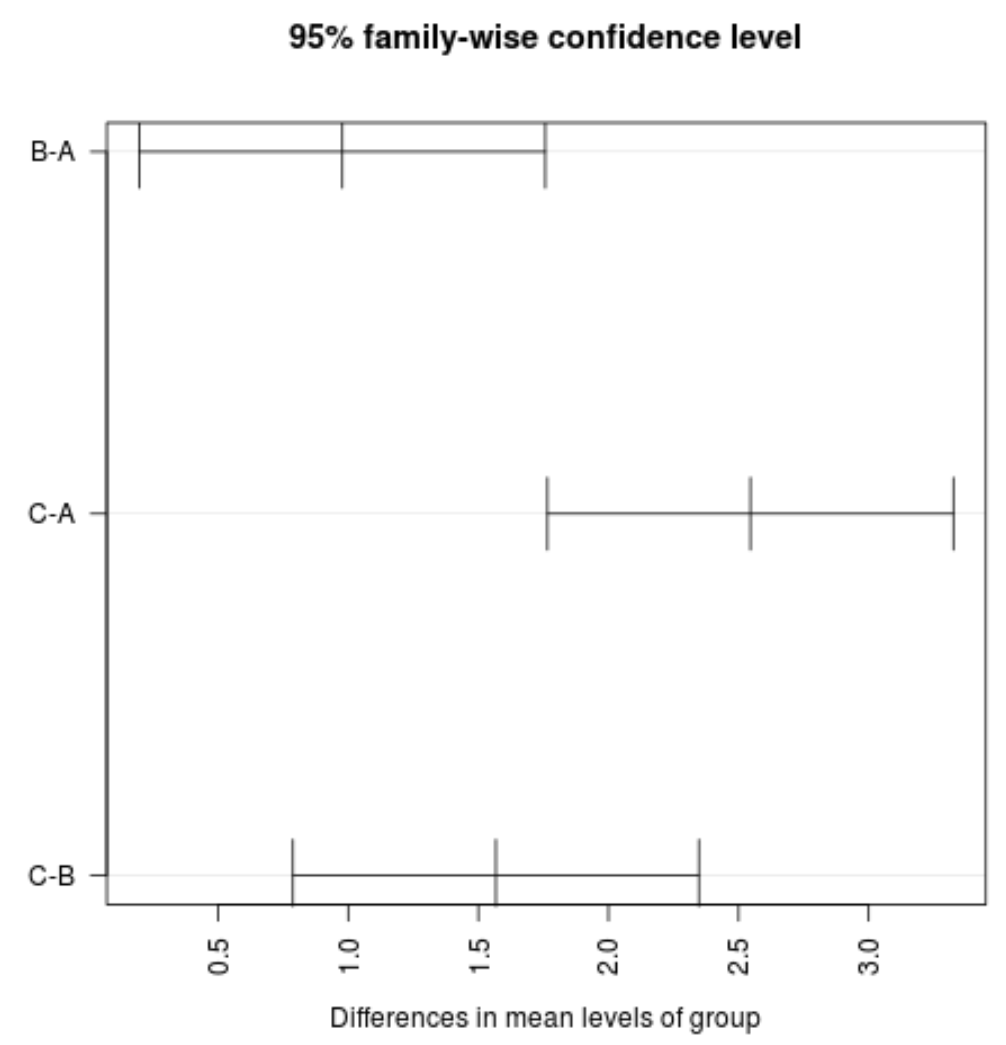
We kunnen zien dat geen van de betrouwbaarheidsintervallen voor de gemiddelde waarde tussen de groepen de waarde nul bevat, wat aangeeft dat er een statistisch significant verschil is in het gemiddelde verlies tussen de drie groepen. Dit komt overeen met het feit dat alle p-waarden voor onze hypothesetoetsen kleiner zijn dan 0,05.

Voor dit specifieke voorbeeld kunnen we het volgende concluderen:

• De gemiddelde waarden van groep C zijn aanzienlijk hoger dan de gemiddelde waarden van de groepen A en B.
• De gemiddelde waarden van groep B zijn aanzienlijk hoger dan de gemiddelde waarden van groep A.

Aanvullende bronnen

Een gids voor het gebruik van post-hoctesten met ANOVA
Eenrichtings-ANOVA uitvoeren in R
Hoe tweeweg-ANOVA uit te voeren in R