Tukey vs. bonferroni vs. scheffe: welke test moet u gebruiken?

Een eenrichtings-ANOVA wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.

Als de totale p-waarde van de ANOVA-tabel onder een bepaald significantieniveau ligt, hebben we voldoende bewijs om te zeggen dat ten minste één van de groepsgemiddelden verschilt van de andere.

Dit vertelt ons echter niet welke groepen van elkaar verschillen. Dit vertelt ons eenvoudigweg dat niet alle groepsgemiddelden gelijk zijn.

Om precies te weten welke groepen van elkaar verschillen, moeten we eenpost-hoc test uitvoeren die het foutenpercentage per gezin kan controleren.

Drie van de meest gebruikte post-hoc-tests zijn:

• De Tukey-methode
• De Scheffe-methode
• De Bonferroni-methode

Deze tutorial biedt een overzicht van elke methode en instructies over welke post-hoc-test u moet gebruiken, afhankelijk van de situatie.

De Tukey-methode

De post hoc-test van Tukey moet worden gebruikt als u paarsgewijze vergelijkingen tussen groepen wilt maken, wat betekent dat de steekproefomvang van elke groep gelijk is.

Als de steekproefgroottes niet gelijk zijn, kunt u een aangepaste versie van de test gebruiken die bekend staat als de Tukey-Kramer-test.

De term ‚paarsgewijze‘ betekent dat we alleen de gemiddelden van twee groepen tegelijk willen vergelijken.

Stel dat we bijvoorbeeld drie groepen hebben: A, B, C.

De post-hoc-test van Tukey zou ons in staat stellen de volgende paarsgewijze vergelijkingen te maken:

• _µA = _µB
• _µA = _µC
• _μB = _μC

Merk op dat er voor k groepen in totaal k ( k -1)/2 mogelijke paarsgewijze vergelijkingen zijn.

De Scheffe-methode

De post-hoc-test van Scheffe moet worden gebruikt als we alle mogelijke contrasten tussen de groepsgemiddelden willen maken. Met deze test kunt u meer dan twee gemiddelden tegelijk vergelijken, in tegenstelling tot de post-hoc-test van Tukey.

Stel dat we bijvoorbeeld vier groepen hebben: A, B, C, D.

De post-hoc-test van Scheffe zou het mogelijk maken complexe vergelijkingen te maken, zoals:

• _μA – _μB = _μC – _μD
• _μA + _μD = _μB + _μC

Hoewel de post-hoctest van Scheffe de meest flexibele is, is deze ook de meest conservatieve en levert deze de breedste betrouwbaarheidsintervallen op. Dit betekent dat het de laagste statistische kracht heeft en het laagste vermogen om echte verschillen tussen groepen te detecteren.

Merk op dat de post-hoc-test van Scheffe kan worden gebruikt, ongeacht of de groepssteekproefgroottes gelijk zijn of niet.

De Bonferroni-methode

De post-hoc-test van Bonferroni moet worden gebruikt als u vooraf een reeks geplande vergelijkingen wilt uitvoeren.

Stel dat we bijvoorbeeld drie groepen hebben – A, B, C – en we weten van tevoren dat we alleen geïnteresseerd zijn in de volgende vergelijkingen:

• _µA = _µB
• _μB = _μC

Als we een specifieke reeks geplande vergelijkingen hebben die we op deze manier van tevoren willen uitvoeren, levert de post-hoctest van Bonferroni de smalste betrouwbaarheidsintervallen op, wat betekent dat deze het grootste vermogen heeft om het werkelijke verschil tussen belangengroepen te detecteren. .

Merk op dat de post-hoc-test van Bonferroni ook kan worden gebruikt, ongeacht of de groepssteekproefgroottes gelijk zijn of niet.

Welke methode moet je gebruiken?

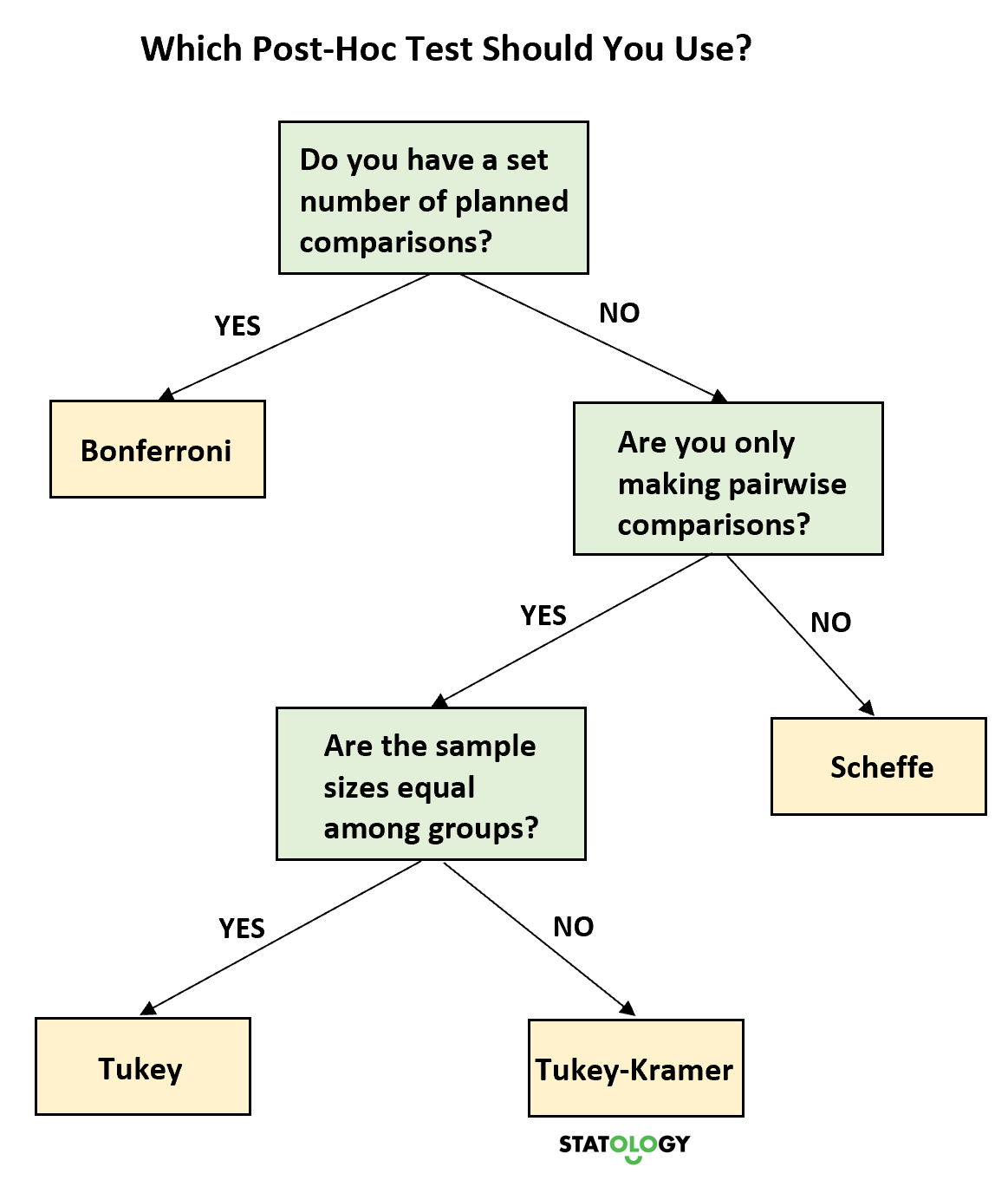
De volgende beslissingsboom helpt u beslissen welke post-hoc-test u moet gebruiken, afhankelijk van de situatie:

Laatste gedachten

Welke post-hoctest u ook kiest, u moet beslissen voordat u het experiment uitvoert.

Dit voorkomt dat je na het experiment een post-hoc test kiest die waarschijnlijk significantere resultaten zou opleveren, wat als een oneerlijke onderzoekspraktijk wordt beschouwd.

Hoe dan ook, de meeste statistische software is in staat om deze post-hoc tests uit te voeren, zodat u ze zelden handmatig hoeft te berekenen.