Een t-test met twee steekproeven uitvoeren in excel

Een t-test met twee steekproeven wordt gebruikt om te testen of de gemiddelden van twee populaties gelijk zijn of niet.

In deze zelfstudie wordt uitgelegd hoe u een t-test met twee steekproeven uitvoert in Excel.

Een t-test met twee steekproeven uitvoeren in Excel

Stel dat onderzoekers willen weten of twee verschillende plantensoorten in een bepaald land dezelfde gemiddelde hoogte hebben. Omdat het te lang zou duren om elke plant te meten, besloten ze een monster van twintig planten van elke soort te nemen.

De volgende afbeelding toont de hoogte (in inches) van elke plant in elk monster:

We kunnen een t-test met twee steekproeven uitvoeren om te bepalen of de twee soorten dezelfde gemiddelde lengte hebben door deze stappen te volgen:

Stap 1: Bepaal of de populatievarianties gelijk zijn .

Wanneer we een t-test met twee steekproeven uitvoeren, moeten we eerst beslissen of we aannemen dat de twee populaties gelijke of ongelijke varianties hebben. Over het algemeen kunnen we aannemen dat populaties gelijke varianties hebben als de verhouding tussen de grootste steekproefvariantie en de kleinste steekproefvariantie kleiner is dan 4:1.

We kunnen de variantie voor elk voorbeeld vinden met behulp van de Excel-functie =VAR.S(Celbereik) , zoals weergegeven in de volgende afbeelding:

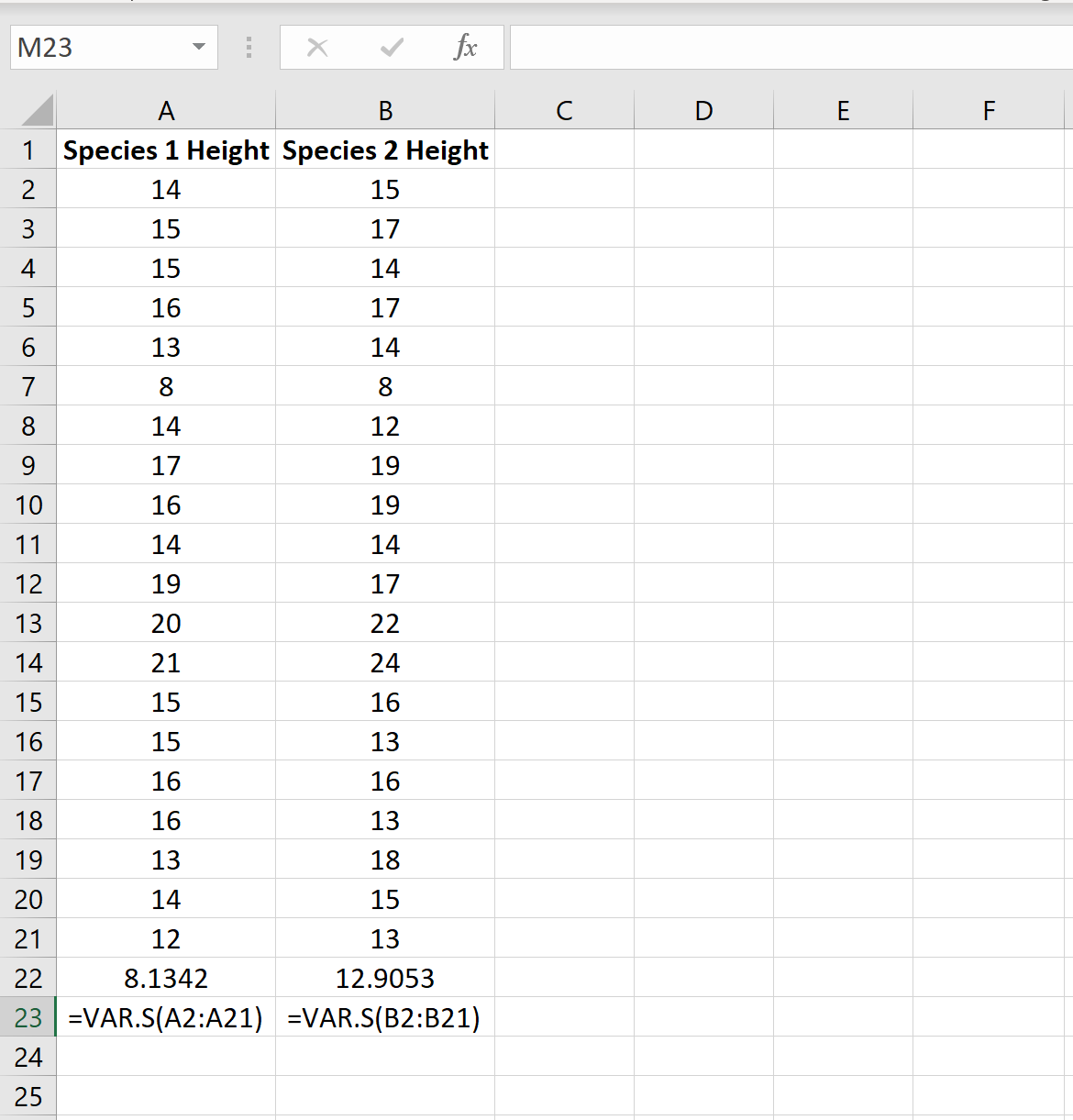
De verhouding tussen de grootste steekproefvariantie en de kleinste steekproefvariantie is 12,9053/8,1342 = 1,586 , wat kleiner is dan 4. Dit betekent dat we kunnen aannemen dat de populatievarianties gelijk zijn.

Stap 2: Open het Analysis ToolPak .

Klik op het tabblad Gegevens van het bovenste lint op ‚Gegevensanalyse‘.

Als u deze optie om te klikken niet ziet, moet u eerst het Analysis ToolPak downloaden , dat volledig gratis is.

Stap 3: Selecteer de juiste test die u wilt gebruiken.

Selecteer de optie met de tekst t-test: twee steekproeven waarbij gelijke varianties worden aangenomen en klik vervolgens op OK.

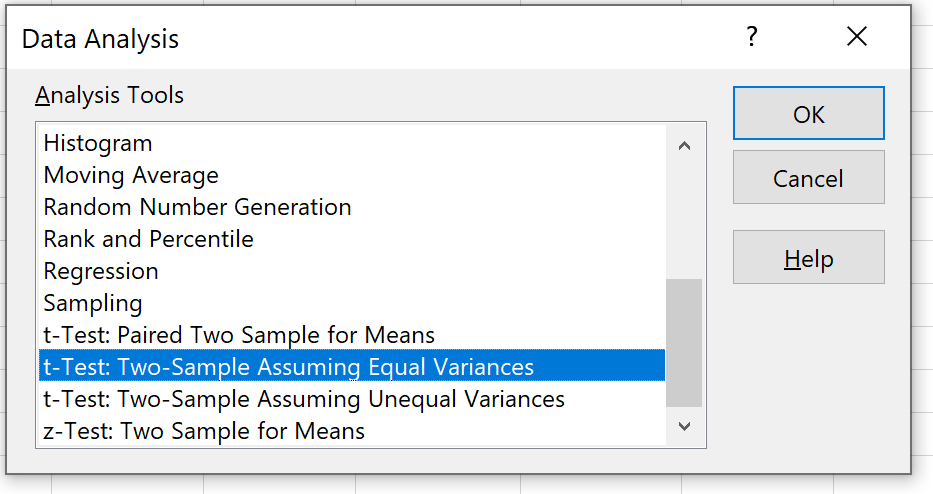
Stap 4: Voer de benodigde gegevens in .

Voer het waardenbereik in voor variabele 1 (onze eerste steekproef), variabele 2 (onze tweede steekproef), het hypothetische gemiddelde verschil (in dit geval plaatsen we „0“ omdat we willen weten of het werkelijke populatiegemiddelde verschil 0 is) en het uitvoerbereik waarin we de t-testresultaten graag weergegeven willen zien. Klik vervolgens op OK.

Stap 5: Interpreteer de resultaten .

Zodra u in de vorige stap op OK klikt, worden de t-testresultaten weergegeven.

Zo interpreteert u de resultaten:

Gemiddelde: Dit is het gemiddelde van elk monster. Monster 1 heeft een gemiddelde lengte van 15,15 en monster 2 heeft een gemiddelde lengte van 15,8 .

Variantie: Dit is de variantie voor elk monster. Monster 1 heeft een variantie van 8,13 en monster 2 heeft een variantie van 12,90 .

Waarnemingen: Dit is het aantal waarnemingen in elk monster. Beide monsters bevatten 20 waarnemingen (bijvoorbeeld 20 individuele planten in elk monster).

Gepoolde variantie: getal berekend door de varianties van elke steekproef te “poolen” met behulp van de formule s ² _p = [ (n ₁ -1)s ² ₁ + (n ₂ -1)s ² ₂ ] / (n ₁ +n ₂ – 2), wat 10,51974 blijkt te zijn. Dit getal wordt vervolgens gebruikt bij het berekenen van de t -teststatistiek.

Hypothetisch gemiddeld verschil: Het getal waarover we ‘hypotheseren’ is het verschil tussen de gemiddelden van de twee populaties. In dit geval hebben we 0 gekozen omdat we willen testen of het verschil tussen de gemiddelden van de twee populaties gelijk is aan 0, bijvoorbeeld of er geen verschil is.

df: De vrijheidsgraden voor de t-toets, berekend als n ₁ + n ₂ -2 = 20 + 20 – 2 = 38 .

t Stat: De teststatistiek t , berekend als t = [ x ₁ – x ₂ ] / √ [s ² _p (1/n ₁ + 1/n ₂ )]

In dit geval is t = [15,15-15,8] / √ [10,51974(1/20+1/20)] = -0,63374 .

Tweezijdige P(T<=t): de p-waarde voor een tweezijdige t-toets. In dit geval is p = 0,530047 . Dit is veel groter dan alfa = 0,05, dus we slagen er niet in de nulhypothese te verwerpen. We hebben niet voldoende bewijs om te zeggen dat de gemiddelden van de twee populaties verschillend zijn.

t Tweezijdig kritisch: Dit is de kritische waarde van de test, gevonden door de waarde in de t-verdelingstabel te identificeren die overeenkomt met een tweezijdige test met alpha = 0,05 en df = 38. Dit blijkt 2 te zijn, 024394 . Omdat onze t- teststatistiek kleiner is dan deze waarde, slagen we er niet in de nulhypothese te verwerpen. We hebben niet voldoende bewijs om te zeggen dat de gemiddelden van de twee populaties verschillend zijn.

Merk op dat de p-waarde en de kritische-waardebenadering beide tot dezelfde conclusie zullen leiden.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere typen t-tests in Excel kunt uitvoeren:

Hoe u een t-test met één monster uitvoert in Excel
Een t-test met gepaarde monsters uitvoeren in Excel