Hoe u een t-test met twee steekproeven uitvoert in spss

Een t-test met twee steekproeven wordt gebruikt om te testen of de gemiddelden van twee populaties gelijk zijn of niet.

In deze tutorial wordt uitgelegd hoe u een t-test met twee steekproeven uitvoert in SPSS.

Voorbeeld: T-test met twee steekproeven in SPSS

Onderzoekers willen weten of een nieuwe brandstofbehandeling een verandering in het gemiddelde aantal kilometers per gallon van een bepaalde auto veroorzaakt. Om dit te testen voeren ze een experiment uit waarbij 12 auto’s de nieuwe brandstofbehandeling krijgen en 12 auto’s niet.

De volgende schermafbeelding toont het mpg van elke auto samen met de groep waartoe deze behoort (0 = geen brandstofbehandeling, 1 = brandstofbehandeling):

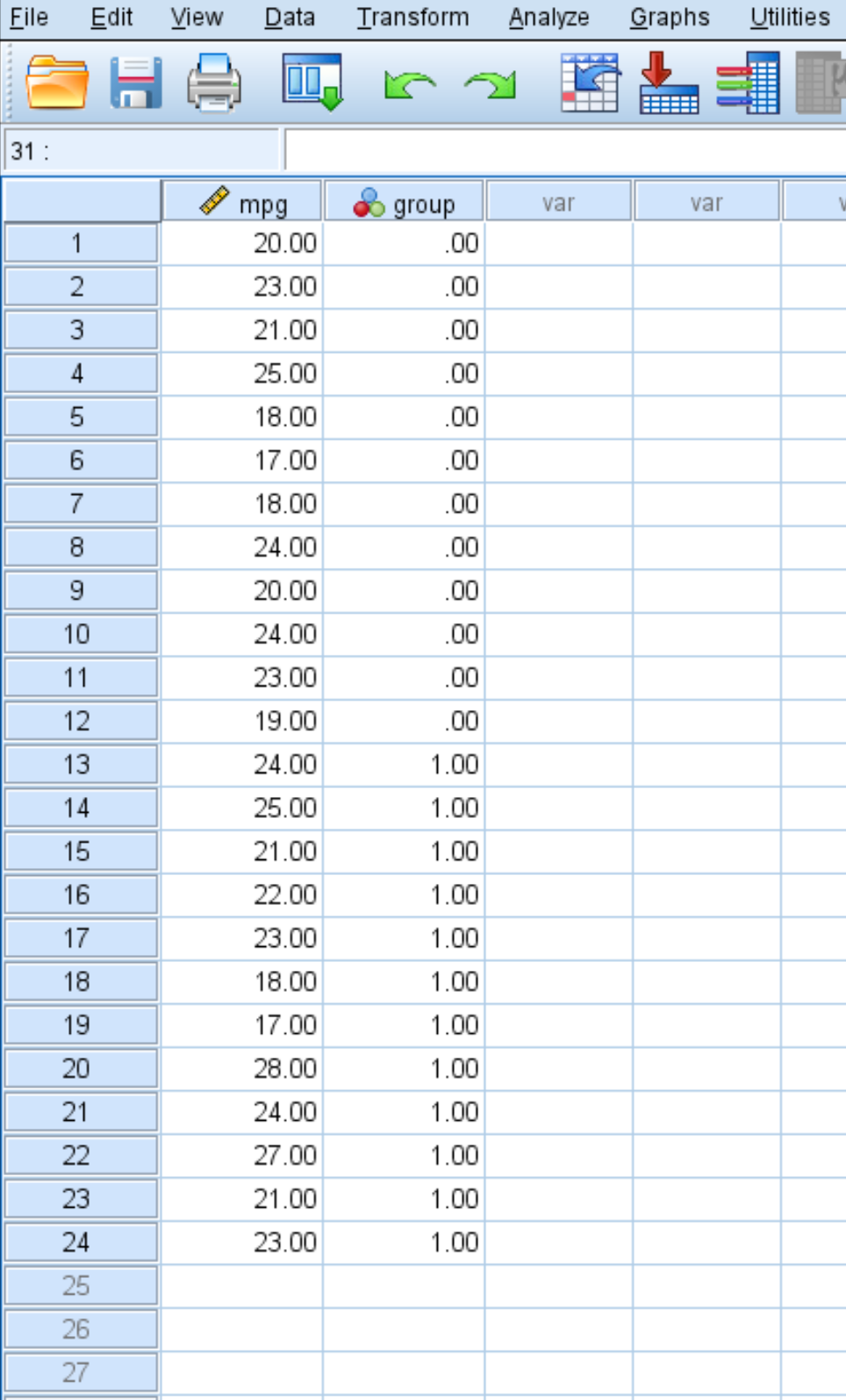
Gebruik de volgende stappen om een t-test met twee steekproeven uit te voeren om te bepalen of er een verschil is in de gemiddelde mpg tussen deze twee groepen, op basis van de volgende nul- en alternatieve hypothesen:

• H ₀ : μ ₁ = μ ₂ (de gemiddelde mpg tussen de twee populaties is gelijk)
• H ₁ : μ ₁ ≠ μ ₂ (de gemiddelde mpg tussen de twee populaties is niet gelijk)

Gebruik een significantieniveau van α = 0,05.

Stap 1: Kies de optie Independent Samples T Test.

Klik op het tabblad Analyseren , vervolgens op Vergelijk middelen en vervolgens op Onafhankelijke monsters T-Test :

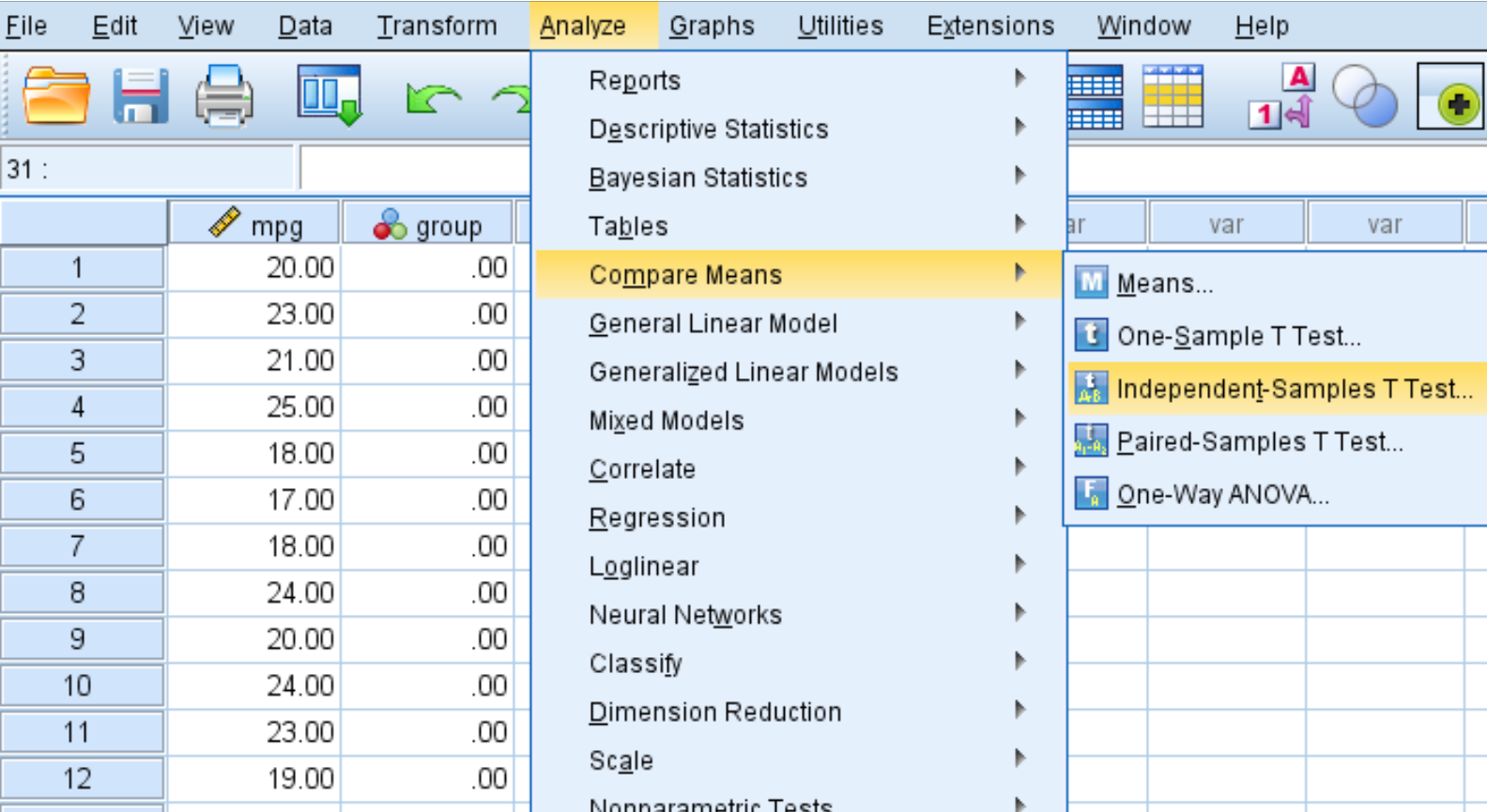
Stap 2: Vul de waarden in die nodig zijn om de t-test met twee steekproeven uit te voeren.

Zodra u op Independent-Samples T Test klikt, verschijnt het volgende venster:

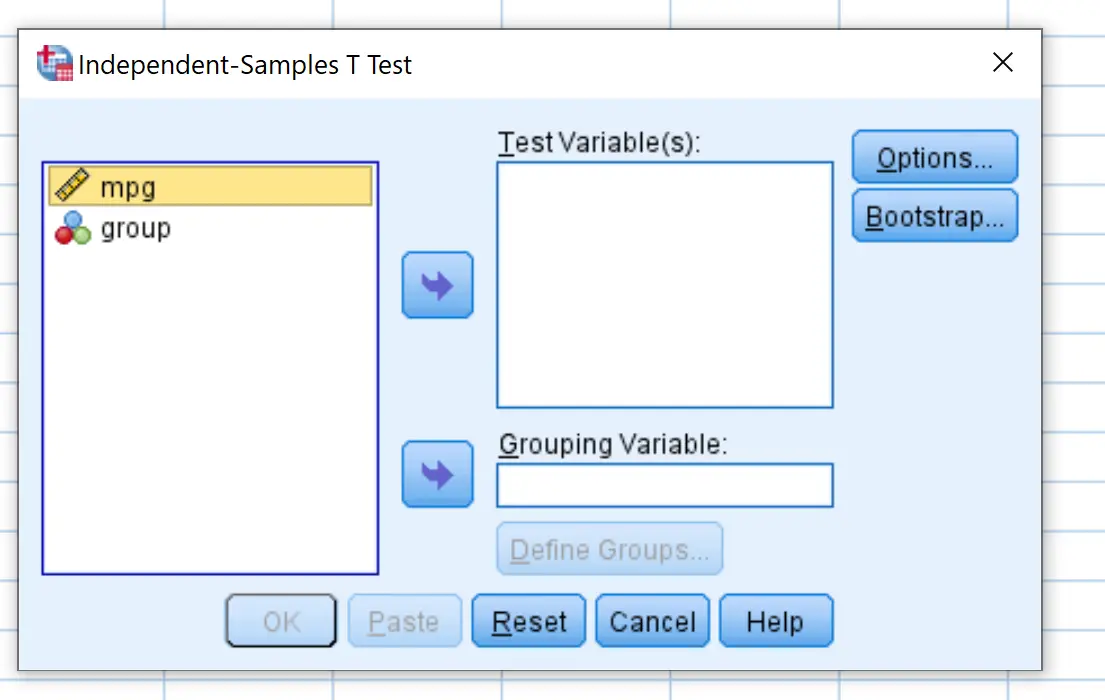
Sleep de mpg naar het vak met de naam Test Variable(s) en groepeer deze in het vak met de naam Grouping Variable . Klik vervolgens op Groepen definiëren en definieer Groep 1 als de rijen met waarde 0 en definieer Groep 2 als de rijen met waarde 1. Klik vervolgens op OK .

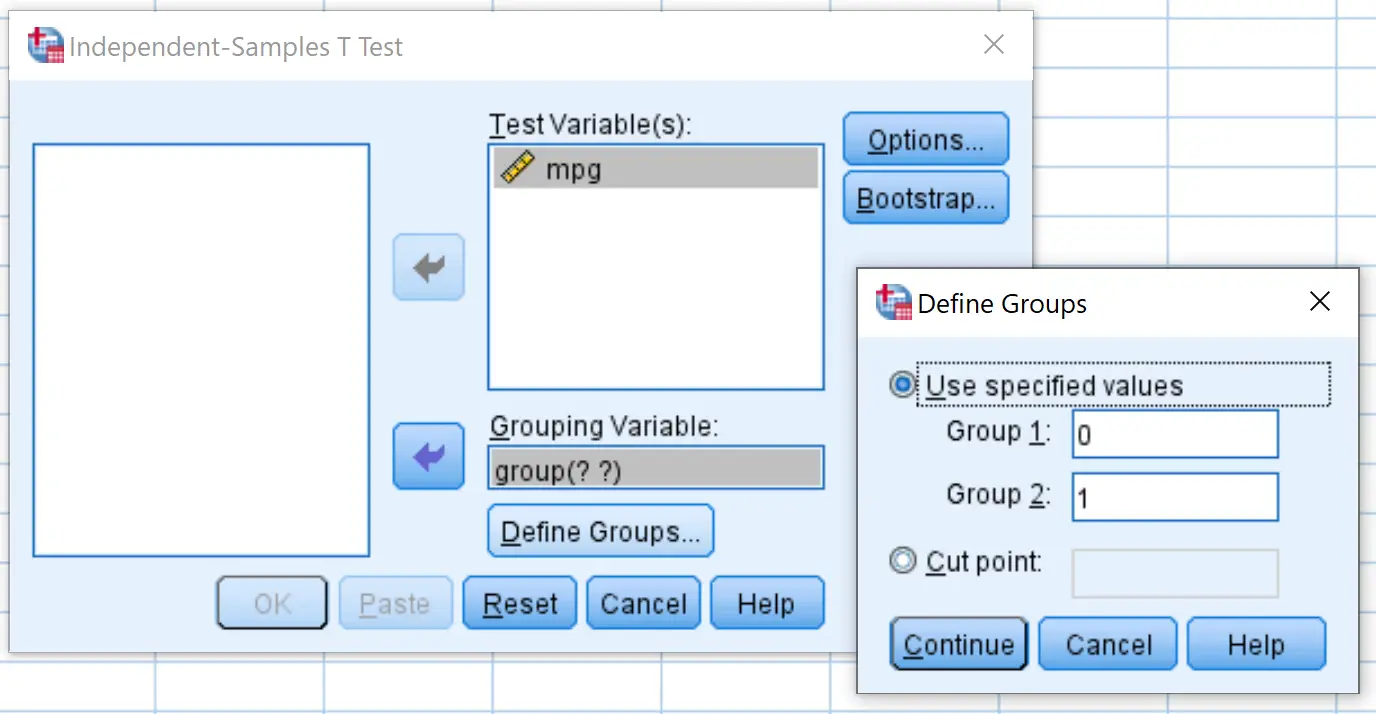
Stap 3: Interpreteer de resultaten.

Zodra u op OK klikt, worden de resultaten van de twee voorbeeld-t-tests weergegeven:

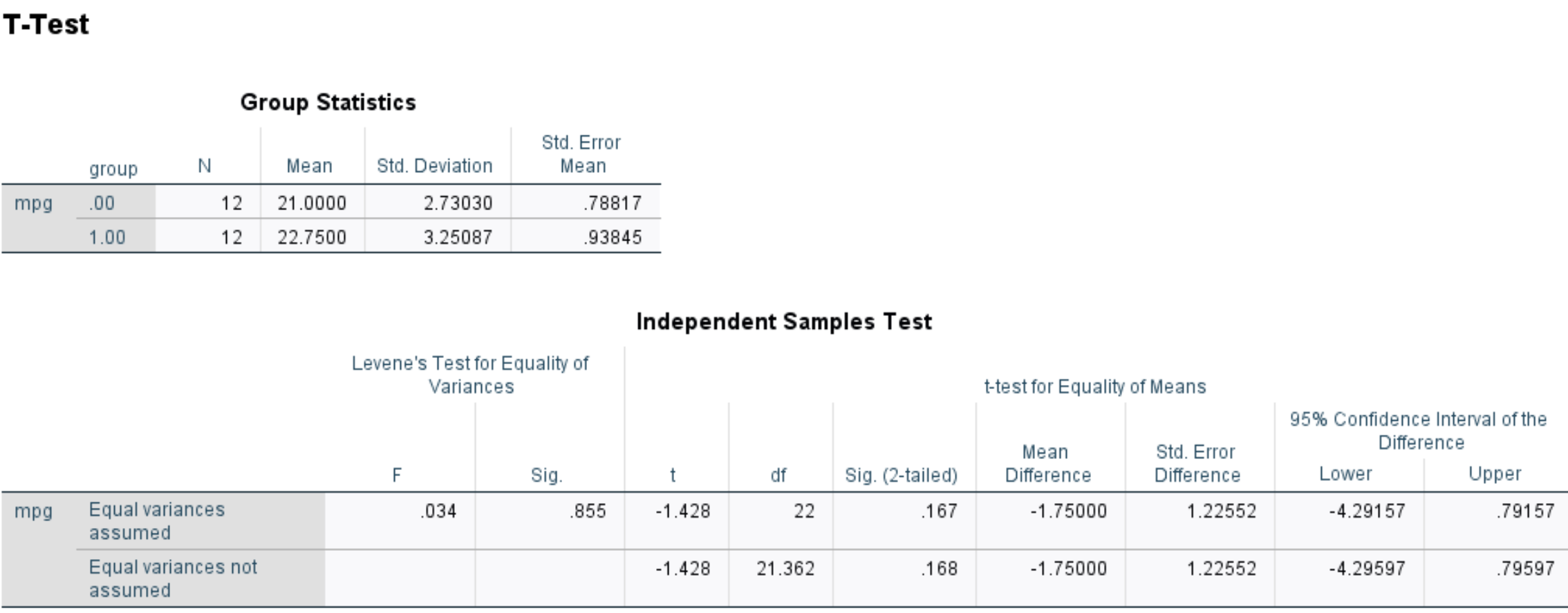
De eerste tabel toont de volgende samenvattende statistieken voor de twee groepen:

• N: Steekproefomvang
• Gemiddeld: het gemiddelde mpg van auto’s in elke groep
• Standaard. Afwijking: de standaardafwijking van de mpg van de auto’s in elke groep
• Standaard. Gemiddelde fout: standaardfout van gemiddelde mpg, berekend in s/√n

De tweede tabel toont de resultaten van de t-test met twee steekproeven. De eerste rij toont de testresultaten als je ervan uitgaat dat de variantie tussen de twee groepen gelijk is. De tweede regel toont de testresultaten als u deze aanname niet maakt.

In dit geval leveren beide versies van de test vrijwel identieke resultaten op. We zullen dus eenvoudigweg verwijzen naar de resultaten van de eerste regel:

• t: De teststatistiek, vastgesteld op -1,428
• df: De vrijheidsgraden, berekend als n ₁ + n ₂ -2 = 12+12-2 = 22
• Zig. (tweezijdig): de tweezijdige p-waarde die overeenkomt met een waarde van -1,428 met df=22
• Gemiddeld verschil: het verschil tussen de twee steekproeven betekent
• Standaard. Verschilfout: de standaardfout van het gemiddelde verschil
• 95% BI van het verschil: 95% betrouwbaarheidsinterval voor het werkelijke verschil tussen de gemiddelden van de twee populaties

Omdat de p-waarde van de test (0,167) niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen. We hebben niet genoeg bewijs om te zeggen dat het werkelijke gemiddelde mpg verschilt tussen auto’s die een behandeling ondergaan en auto’s die dat niet doen.