Hoe u tweerichtings-anova uitvoert in sas

Een tweerichtings-ANOVA wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen die aan twee variabelen zijn toegewezen (soms „factoren“ genoemd).

Deze zelfstudie biedt een stapsgewijs voorbeeld van het uitvoeren van een tweerichtings-ANOVA in SAS.

Stap 1: Creëer de gegevens

Stel dat een botanicus wil weten of de plantengroei wordt beïnvloed door blootstelling aan zonlicht en de frequentie van water geven.

Ze plant 30 zaden en laat ze een maand lang groeien onder verschillende omstandigheden van blootstelling aan de zon en waterfrequentie. Na een maand registreert ze de hoogte van elke plant. De resultaten worden hieronder weergegeven:

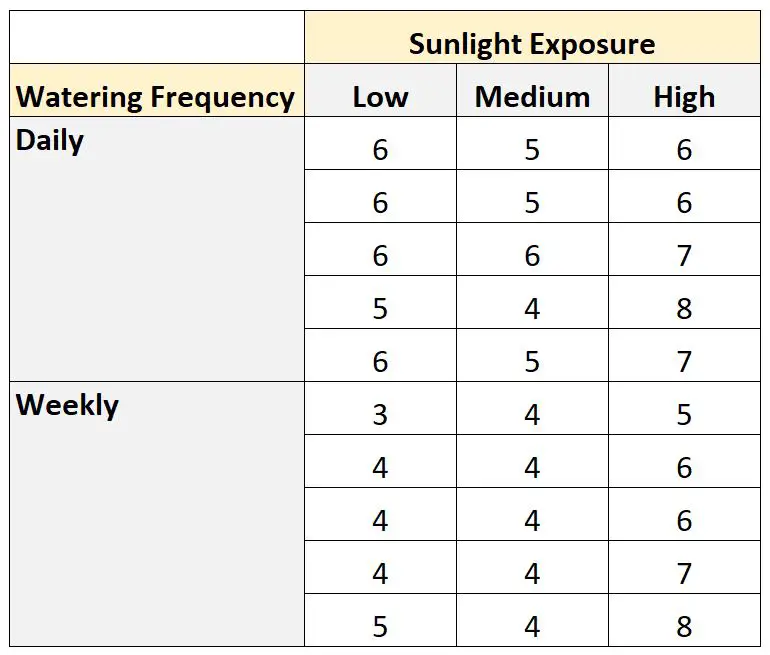
We kunnen de volgende code gebruiken om deze gegevensset in SAS te maken:

 /*create dataset*/
data my_data;
    input water $sunlight $height;
    datalines ;
daily low 6
daily low 6
daily low 6
daily low 5
daily low 6
daily med 5
daily med 5
daily med 6
daily med 4
daily med 5
daily high 6
daily high 6
daily high 7
daily high 8
daily high 7
weekly low 3
weekly low 4
weekly low 4
weekly low 4
weekly low 5
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly high 5
weekly high 6
weekly high 6
weekly high 7
weekly high 8
;
run ;

Stap 2: Voer de tweeweg-ANOVA uit

Vervolgens zullen we proc ANOVA gebruiken om de tweerichtings-ANOVA uit te voeren:

 /*perform two-way ANOVA*/
proc ANOVA data =my_data;
class water sunlight;
model height = water sunlight water*sunlight;
means water sunlight / tukey cldiff ;
run ;

Stap 3: Interpreteer de resultaten

De eerste tabel die we in de resultaten willen analyseren is de ANOVA-tabel:

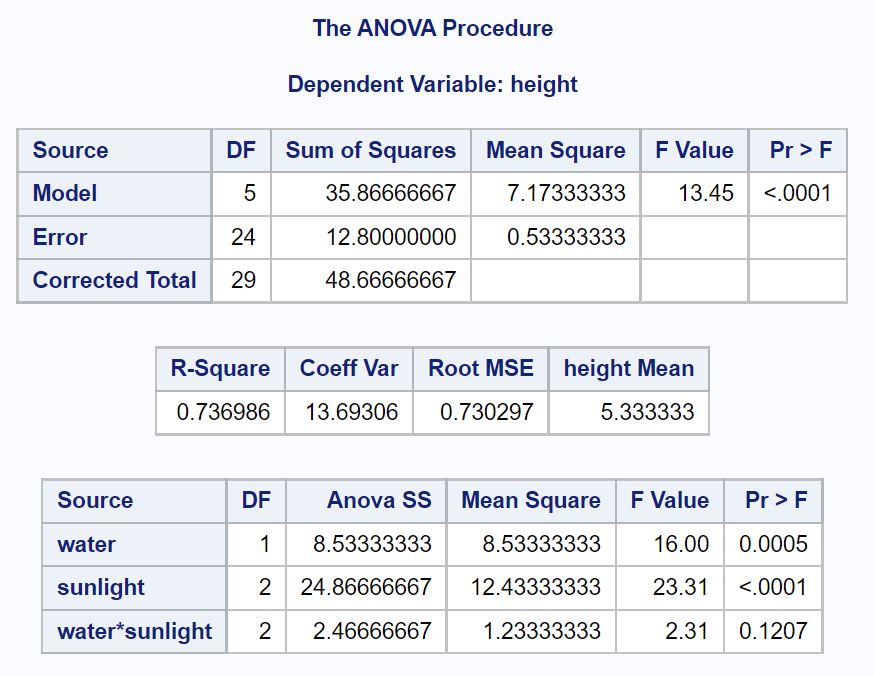
Uit deze tabel kunnen we zien:

• De p-waarde voor water: 0,0005
• De p-waarde voor zonlicht: <.0001
• De p-waarde voor de interactie tussen water en zonlicht: . 1207

Dit vertelt ons dat water en zonlicht statistisch significante voorspellers zijn van de planthoogte en dat er geen statistisch significant interactie-effect is tussen water en zonlicht.

Vervolgens kunnen we de resultaten van de post-hoctests van Tukey onderzoeken om te bepalen welke water- en zonlichtniveaus statistisch significant verschillen.

Eerst zullen we kijken naar de post-hocvergelijkingen van Tukey voor water:

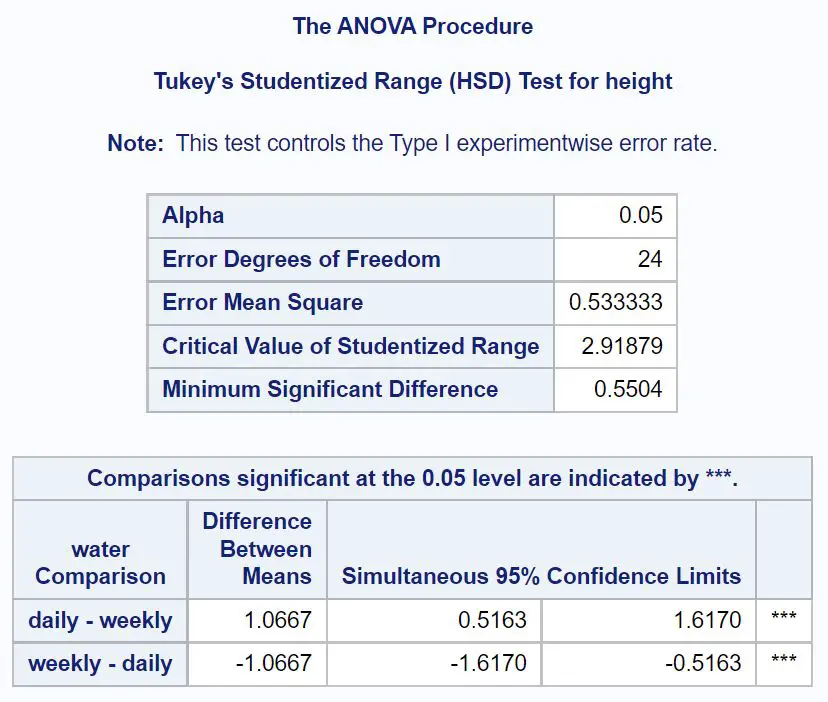
Uit de resultaten kunnen we zien dat het gemiddelde hoogteverschil tussen planten die dagelijks en wekelijks water kregen 1,0667 inch bedroeg.

Het 95% betrouwbaarheidsinterval voor het verschil in gemiddelde grootte is [.5163, 1.6170] . Dit betekent dat we er 95% zeker van zijn dat het werkelijke verschil in gemiddelde hoogte tussen planten die dagelijks water krijgen en planten die wekelijks water krijgen, tussen 0,5163 inch en 1,6170 inch ligt.

Eerst zullen we kijken naar de post-hocvergelijkingen van Tukey voor zonlicht:

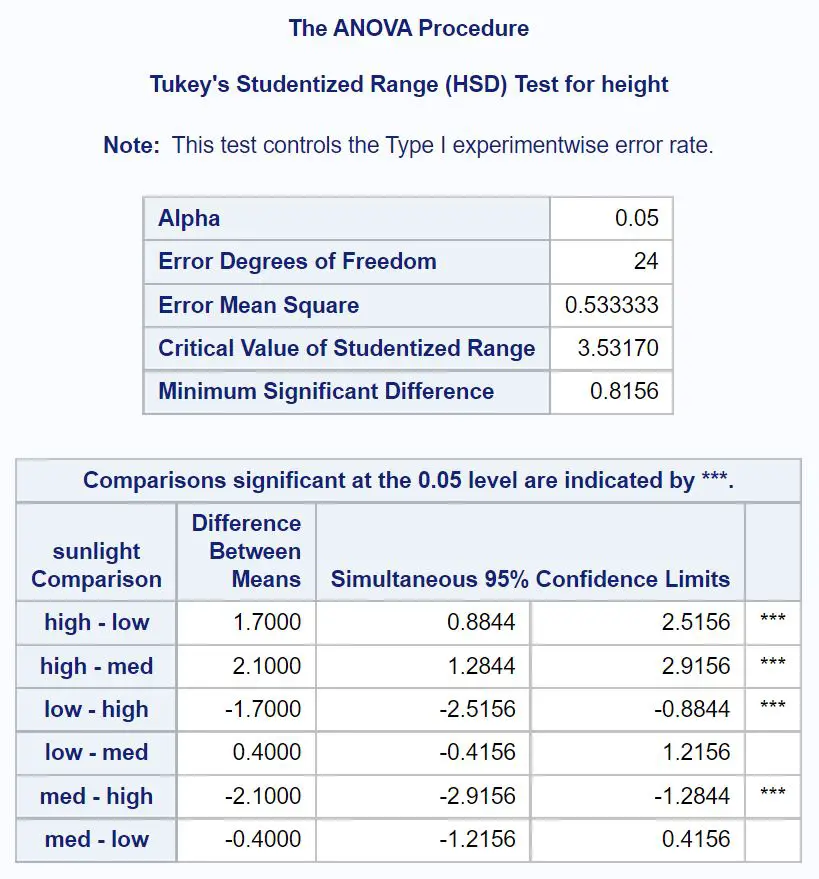
Om erachter te komen welke groepsgemiddelden verschillend zijn, moeten we kijken naar welke paarsgewijze vergelijkingen sterren ( *** ) ernaast hebben.

Uit de tabel kunnen we zien dat de gemiddelden van de volgende groepen statistisch significant verschillen:

• Veel of weinig zonneschijn (95% BI = [.8844, 2.5156])
• Veel zonneschijn of middelmatige zonneschijn (95% BI = [1,2844, 2,9156])

Stap 4: Rapporteer resultaten

Ten slotte kunnen we de resultaten van de tweerichtings-ANOVA rapporteren :

Er werd een tweeweg-ANOVA uitgevoerd om het effect van de waterfrequentie en de blootstelling aan de zon op de plantengroei te analyseren.

Uit een tweeweg-ANOVA bleek dat er geen statistisch significante interactie was tussen de effecten van de waterfrequentie en de blootstelling aan de zon (p = 0,1207).

Een eenvoudige analyse van handeffecten toonde aan dat de waterfrequentie een statistisch significant effect had op de plantengroei (p = 0,0005).

Een eenvoudige analyse van handeffecten toonde aan dat blootstelling aan de zon ook een statistisch significant effect had op de plantengroei (p < 0,0001).

Aanvullende bronnen

De volgende zelfstudies bieden aanvullende informatie over tweerichtings-ANOVA’s:

Inleiding tot tweerichtings-ANOVA
One-way of two-way ANOVA: wanneer gebruik je ze?
Handmatig een tweerichtings-ANOVA uitvoeren