Hoe u een t-test met twee steekproeven uitvoert op een ti-84-rekenmachine

Een t-test met twee steekproeven wordt gebruikt om te testen of de gemiddelden van twee populaties gelijk zijn of niet.

In deze tutorial wordt uitgelegd hoe u een t-test met twee steekproeven uitvoert op een TI-84-rekenmachine.

Voorbeeld: T-test met twee steekproeven op een TI-84-rekenmachine

Onderzoekers willen weten of een nieuwe brandstofbehandeling een verandering in het gemiddelde mpg van een bepaalde auto veroorzaakt. Om dit te testen voeren ze een experiment uit waarbij 12 auto’s de nieuwe brandstofbehandeling krijgen en 12 auto’s niet. Voor de controlegroep is de gemiddelde mpg 21 mpg en de standaardafwijking 2,73 mpg. Voor de behandelingsgroep is de gemiddelde mpg 22,75 mpg en de standaardafwijking 3,25 mpg.

Gebruik deze gegevens om een t-test met twee steekproeven uit te voeren om te bepalen of de gemiddelde mpg tussen de twee groepen verschillend is.

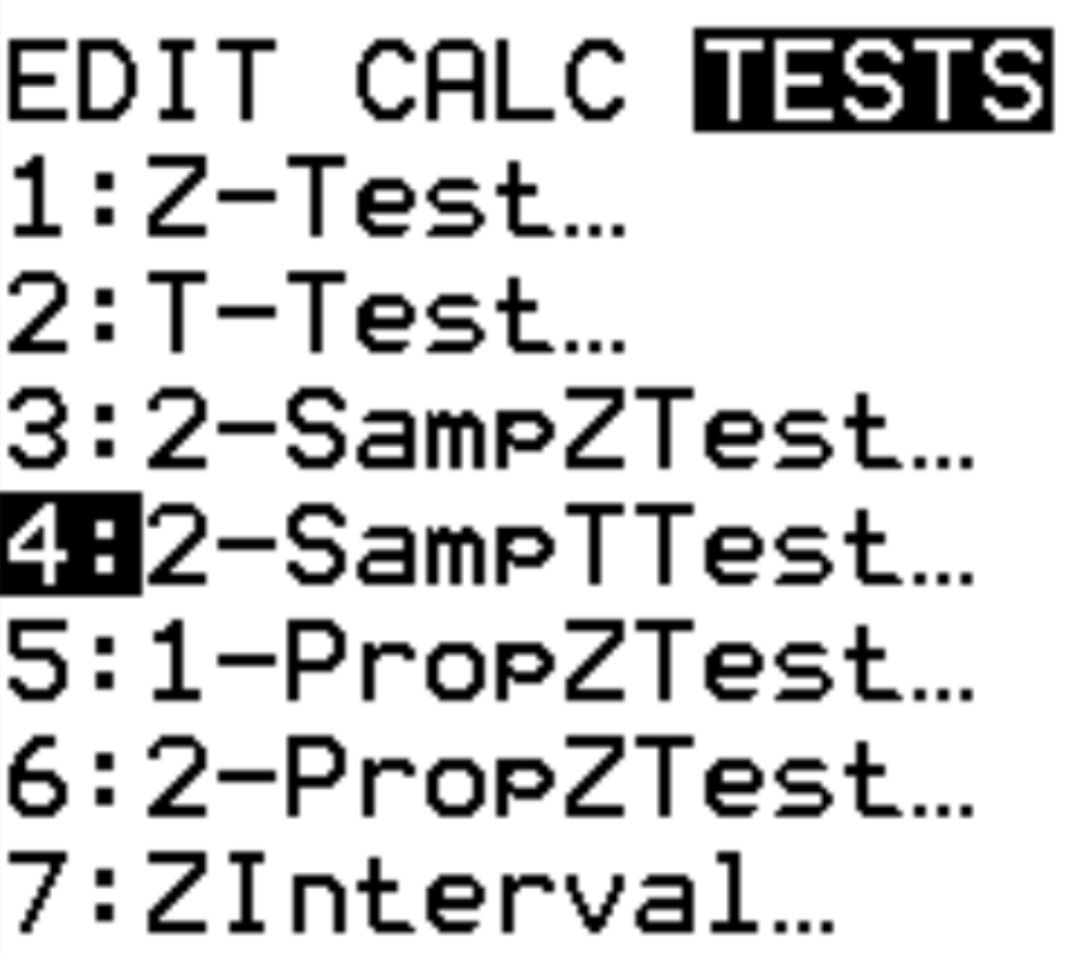
Stap 1: Selecteer 2-SampTTest.

Tik op Stat . Scroll naar beneden naar TESTEN. Blader naar 2-SampTTest en druk op ENTER .

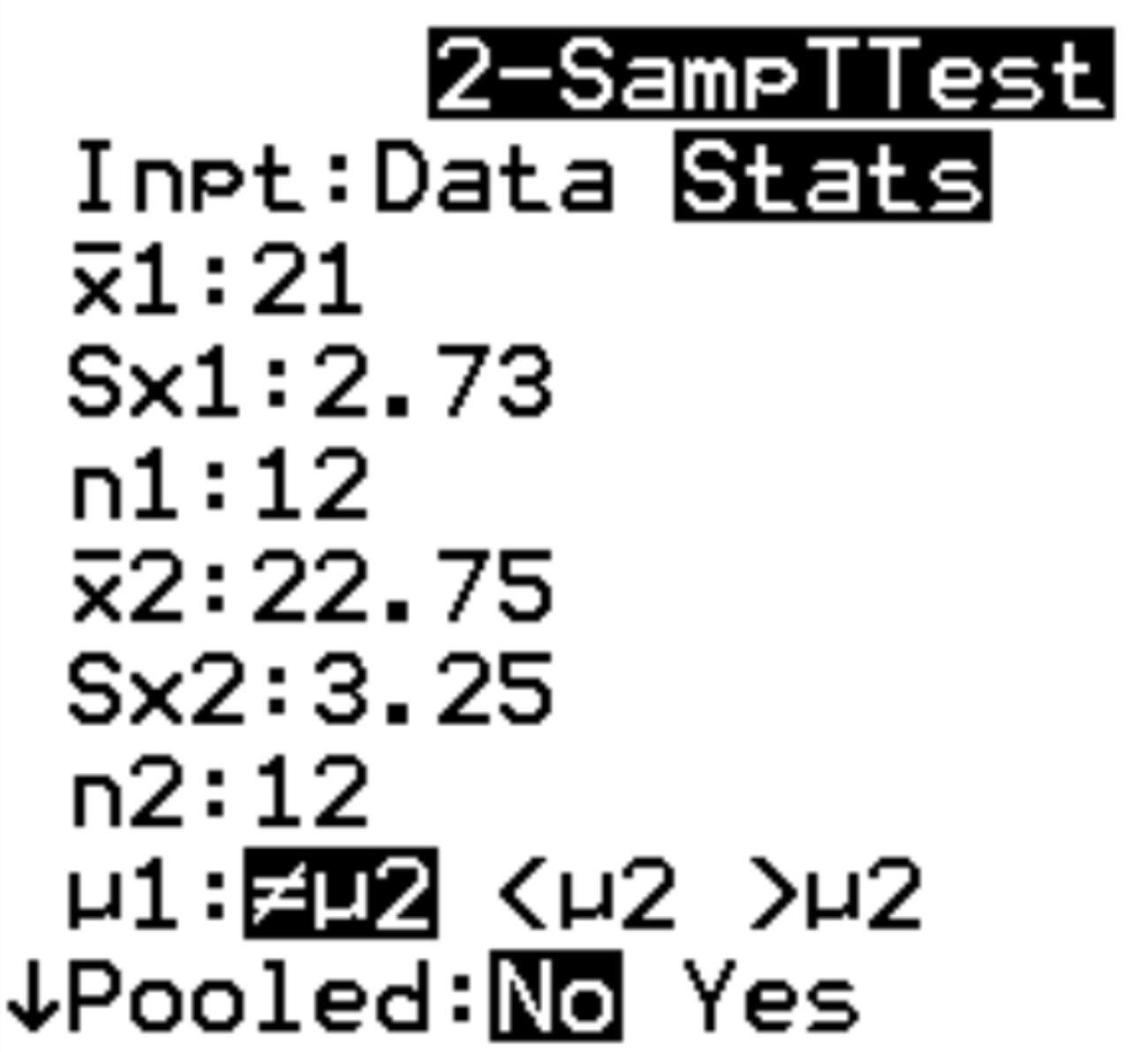
Stap 2: Vul de benodigde gegevens in.

De rekenmachine vraagt om de volgende informatie:

• Invoer: Kies of u met ruwe gegevens (Data) of samenvattende statistieken (Stats) werkt. In dit geval zullen we Statistieken markeren en op ENTER drukken.
• x 1: de steekproefgemiddelden van de eerste groep. We typen 21 en drukken op ENTER .
• Sx1: standaardafwijking van de steekproef van de eerste groep. We typen 2.73 en drukken op ENTER .
• n1: De steekproefomvang van de eerste groep. We typen 12 en drukken op ENTER .
• x 2: het gemiddelde van de steekproef van de tweede groep. We typen 22.75 en drukken op ENTER .
• Sx2: standaardafwijking van de steekproef van de tweede groep. We typen 3.25 en drukken op ENTER .
• n2: de steekproefgrootte van de tweede groep. We typen 12 en drukken op ENTER .
• μ1 : De alternatieve hypothese die moet worden gebruikt. Omdat we een tweezijdige test uitvoeren, zullen we ≠ μ2 markeren en op ENTER drukken. Dit geeft aan dat onze alternatieve hypothese μ1≠μ2 is. De andere twee opties zouden worden gebruikt voor testen links (μ1<μ2) en rechts (μ1>μ2).
• Gepoold: kies of u de gaten van de twee groepen wel of niet wilt samenvoegen. In de meeste gevallen zullen we nee kiezen. Markeer nee en druk op ENTER .

Markeer ten slotte Bereken en druk op ENTER .

Stap 3: Interpreteer de resultaten.

Onze rekenmachine produceert automatisch de resultaten van de twee t-testvoorbeelden:

Zo interpreteert u de resultaten:

• μ ₁ ≠μ ₂ : Dit is de alternatieve hypothese van de test.
• t=-1,42825817 : Dit is de t-teststatistiek.
• p=0,1676749174 : Dit is de p-waarde die overeenkomt met de teststatistiek.
• df=21,36350678: dit zijn de vrijheidsgraden die worden gebruikt om de teststatistiek te berekenen.
• x1 = ₂₁ . Dit is het steekproefgemiddelde dat we voor de eerste groep hebben ingevoerd.
• x ₂ =22,75: Dit is het steekproefgemiddelde dat we voor de tweede groep hebben ingevoerd.
• Sx1=2,73 . Dit is de standaarddeviatie van de steekproef die we voor de eerste groep hebben ingevoerd.
• Sx2=3,25 : Dit is de standaarddeviatie van de steekproef die we voor de tweede groep hebben ingevoerd.
• n1=12: Dit is de steekproefgrootte die we voor de eerste groep hebben ingevoerd.
• n2=12: Dit is de steekproefomvang die we voor de tweede groep hebben ingevoerd.

Omdat de p-waarde van de test (0,1676749174) niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen. Dit betekent dat we niet genoeg bewijs hebben om te zeggen dat de gemiddelde mpg tussen de twee groepen verschillend is.