Hoe u een t-test met twee steekproeven uitvoert in stata

Een t-test met twee steekproeven wordt gebruikt om te testen of de gemiddelden van twee populaties gelijk zijn of niet.

In deze tutorial wordt uitgelegd hoe u een t-test met twee steekproeven uitvoert in Stata.

Voorbeeld: T-test met twee steekproeven in Stata

Onderzoekers willen weten of een nieuwe brandstofbehandeling een verandering in het gemiddelde mpg van een bepaalde auto veroorzaakt. Om dit te testen voeren ze een experiment uit waarbij 12 auto’s de nieuwe brandstofbehandeling krijgen en 12 auto’s niet.

Voer de volgende stappen uit om een t-test met twee steekproeven uit te voeren om te bepalen of er een verschil is in de gemiddelde mpg tussen deze twee groepen.

Stap 1: Gegevens laden.

Laad eerst de gegevens door gebruik https://www.stata-press.com/data/r13/fuel3 in het opdrachtvenster te typen en op Enter te klikken.

Stap 2: Bekijk de onbewerkte gegevens.

Voordat we een t-test met twee steekproeven uitvoeren, kijken we eerst naar de onbewerkte gegevens. Navigeer in de bovenste menubalk naar Gegevens > Gegevenseditor > Gegevenseditor (Bladeren) . De eerste kolom, mpg , toont de mpg voor een bepaalde auto. De tweede kolom, behandeld , geeft aan of de auto wel of niet de brandstofbehandeling heeft ondergaan (0 = nee, 1 = ja).

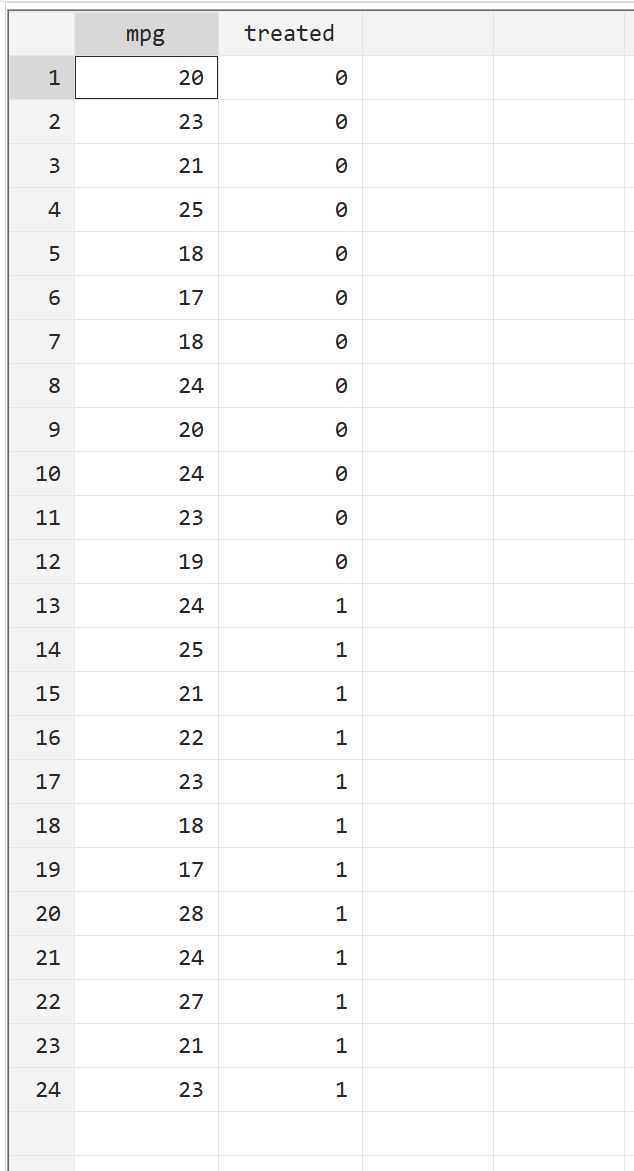
Stap 3: Visualiseer de gegevens.

Laten we vervolgens de gegevens visualiseren. We zullen boxplots maken om de verdeling van mpg-waarden voor elke groep weer te geven.

Ga in de bovenste menubalk naar Grafieken > Boxplot . Kies onder variabelen mpg :

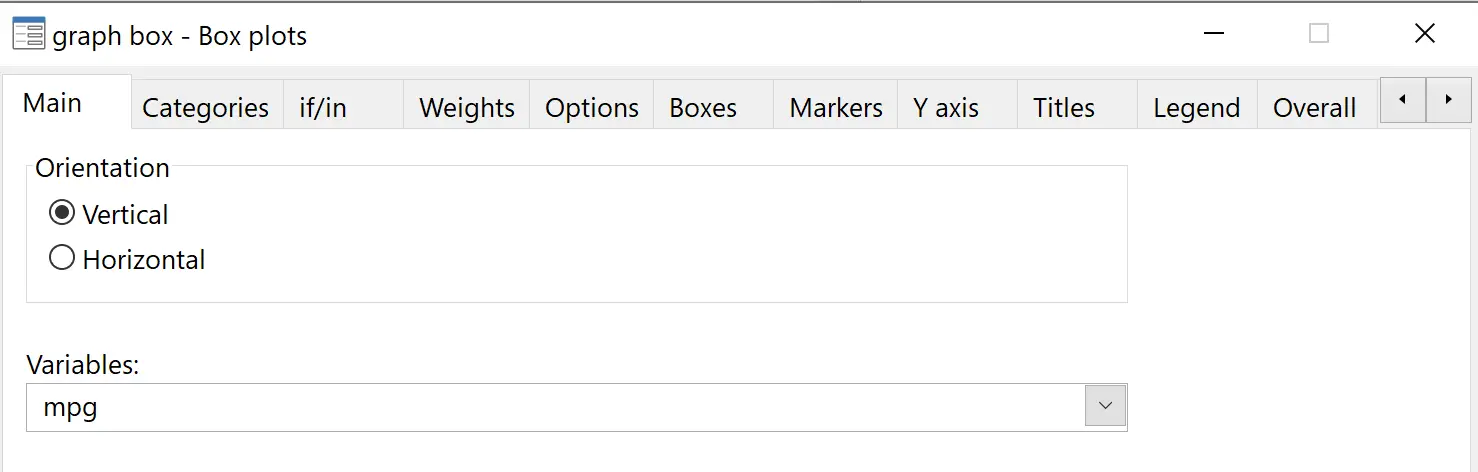
Kies vervolgens in de subkop Categorieën onder Variabele groeperen de optie Verwerkt :

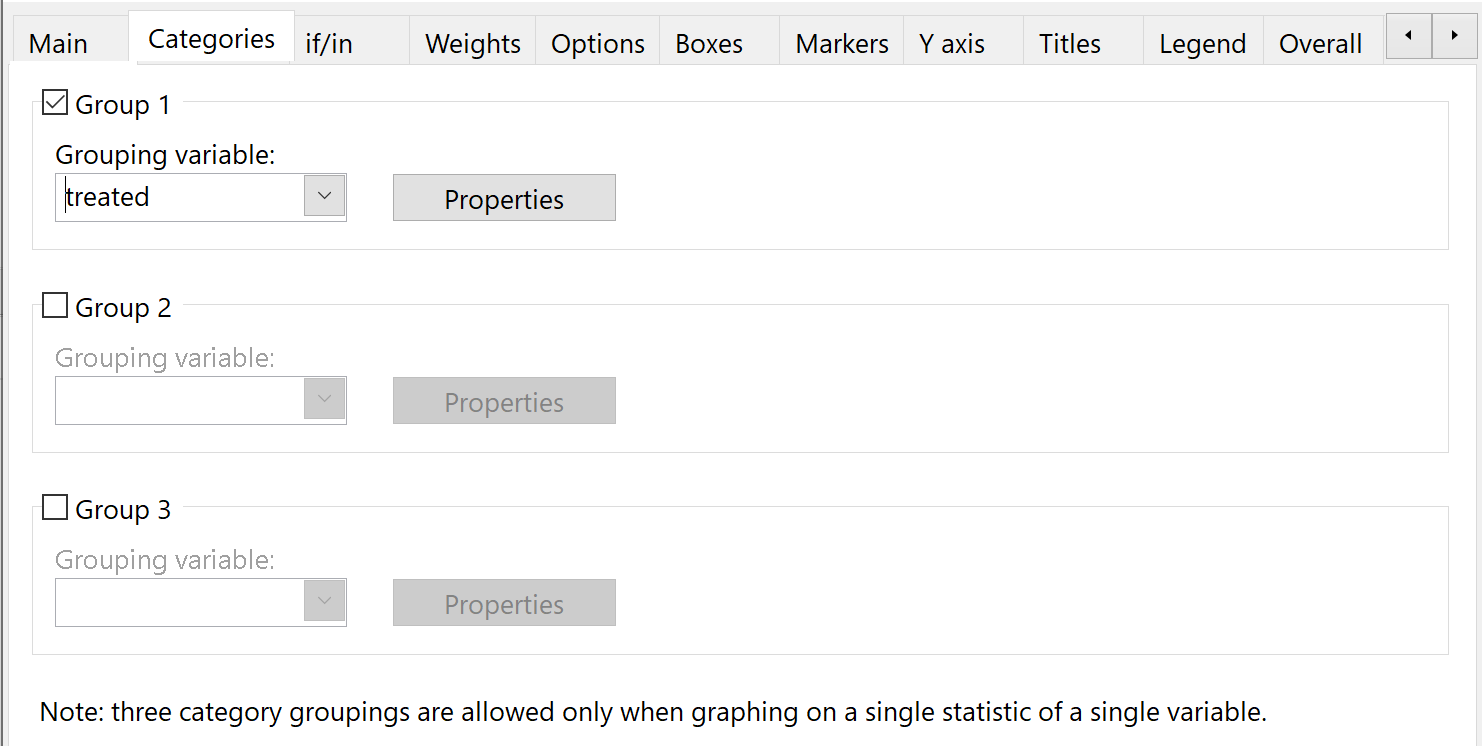
Klik op OK . Er wordt automatisch een diagram met twee boxplots weergegeven:

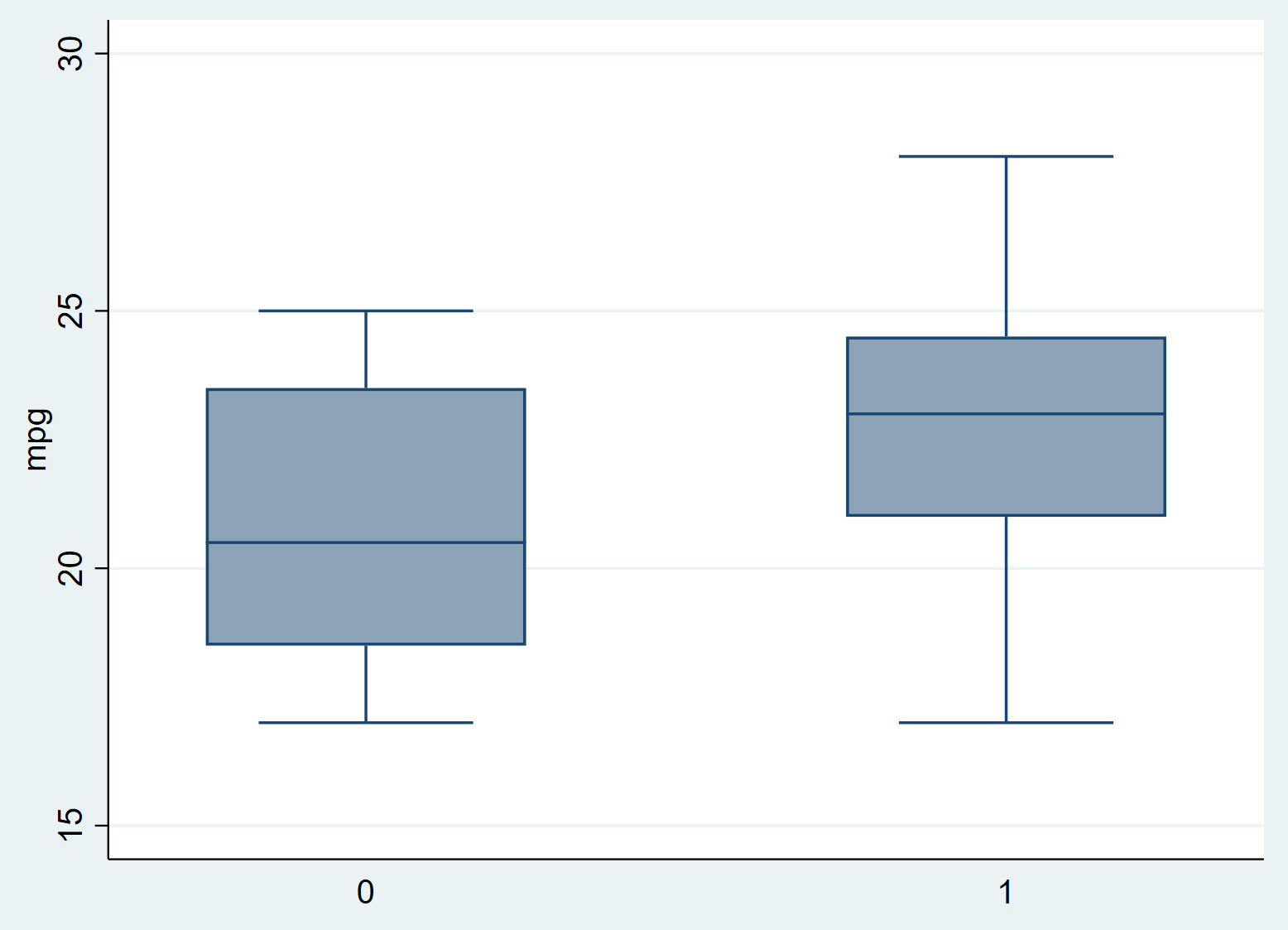
We kunnen meteen zien dat de mpg hoger lijkt te zijn voor de behandelde groep (1) vergeleken met de onbehandelde groep (0), maar we moeten een t-test met twee steekproeven uitvoeren om te zien of deze verschillen statistisch significant zijn. .

Stap 4: Voer een t-test met twee steekproeven uit.

Ga in de menubalk bovenaan naar Statistieken > Samenvattingen, Tabellen & Toetsen > Klassieke hypothesetoetsen > t-Test (vergelijking van gemiddeldentoets) .

Kies Twee voorbeelden met behulp van groepen . Kies mpg bij Variabelenaam. Kies Processed bij Groepsvariabelenaam. Kies bij Betrouwbaarheidsniveau het gewenste niveau. Een waarde van 95 komt overeen met een significantieniveau van 0,05. We laten dit op 95 staan. Klik ten slotte op OK .

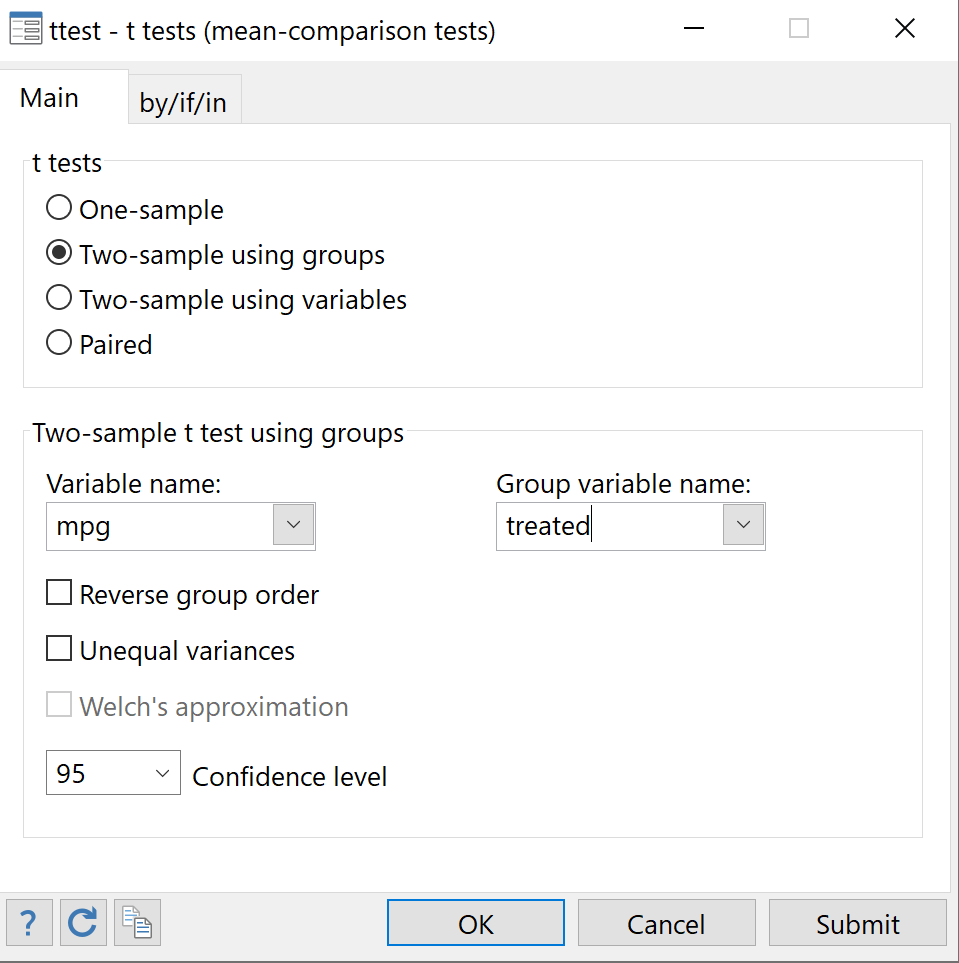
De resultaten van de twee voorbeeld-t-tests worden weergegeven:

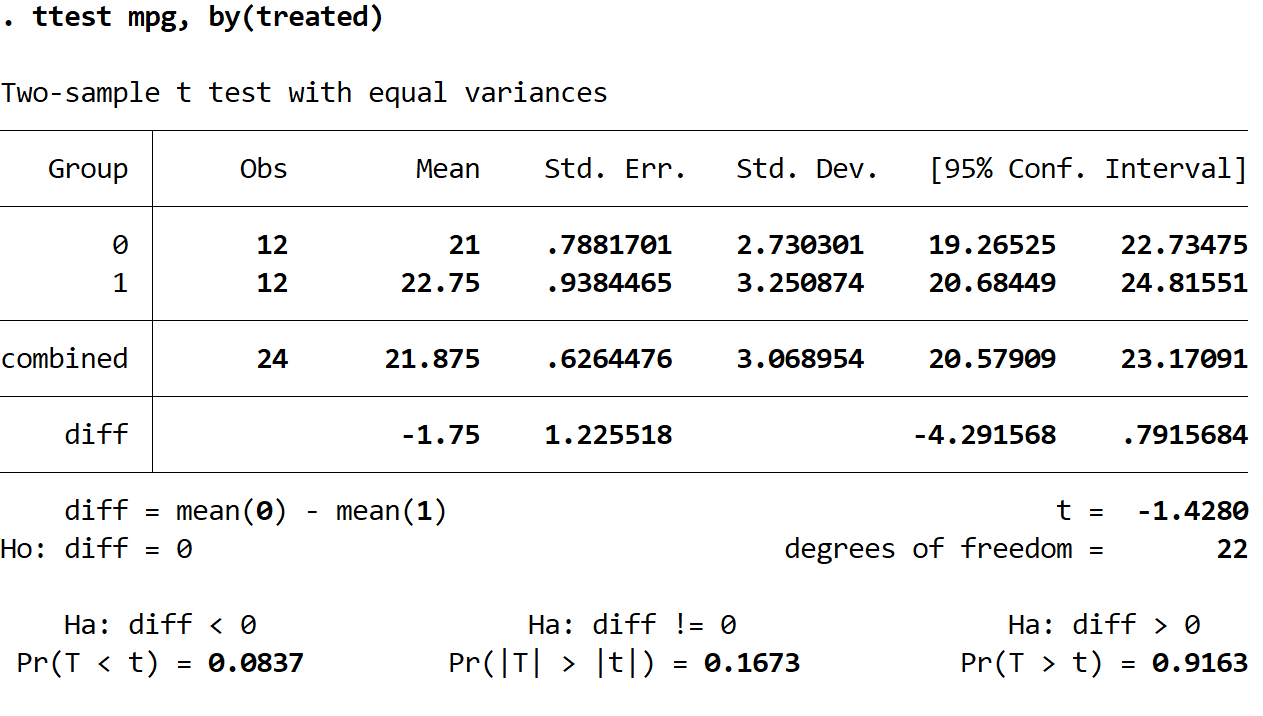
Per groep ontvangen wij de volgende gegevens:

Obs: het aantal waarnemingen. Er zijn 12 observaties in elke groep.

Gemiddeld: de gemiddelde mpg. In groep 0 is het gemiddelde 21. In groep 1 is het gemiddelde 22,75.

Standaard. Err: de standaardfout, berekend als σ / √ n

Standaard. Dev: de standaardafwijking van mpg.

95% Conf. Bereik: 95% betrouwbaarheidsinterval voor het werkelijke populatiegemiddelde in mpg.

t: de teststatistiek van de t-test met twee steekproeven.

Vrijheidsgraden: de vrijheidsgraden die voor de test moeten worden gebruikt, berekend als n-2 = 24-2 = 22.

De p-waarden voor drie verschillende t-toetsen met twee steekproeven worden onderaan de resultaten weergegeven. Omdat we willen begrijpen of de gemiddelde mpg eenvoudigweg verschillend is tussen de twee groepen, zullen we kijken naar de resultaten van de tussenliggende test (waarin de alternatieve hypothese Ha:diff !=0 is), die een p-waarde van 0,1673 heeft. .

Omdat deze waarde niet onder ons significantieniveau van 0,05 ligt, slagen we er niet in de nulhypothese te verwerpen. We hebben niet genoeg bewijs om te zeggen dat het werkelijke gemiddelde mpg tussen de twee groepen verschillend is.

Stap 5: Rapporteer de resultaten.

Ten slotte zullen we de resultaten van onze twee voorbeeld-t-tests rapporteren. Hier is een voorbeeld van hoe u dit kunt doen:

Er werd een T-test met twee monsters uitgevoerd op 24 auto’s om te bepalen of een nieuwe brandstofbehandeling een verschil in het gemiddelde aantal kilometers per gallon veroorzaakte. Elke groep bevatte 12 auto’s.

De resultaten toonden aan dat de gemiddelde mpg niet verschilde tussen de twee groepen (t = -1,428 met df = 22, p = 0,1673) op een significantieniveau van 0,05.

Een betrouwbaarheidsinterval van 95% voor het werkelijke verschil in populatiegemiddelden leverde het interval op van (-4,29, 0,79).