Typen

Von Dr.benjamin anderson August 5, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat het betekent om een verdeling in de statistiek te karakteriseren. Zo vindt u de definitie van typificatie, een voorbeeld van typificatie van een variabele en bovendien kunt u oefenen met een stap voor stap opgeloste oefening.

Wat is typen?

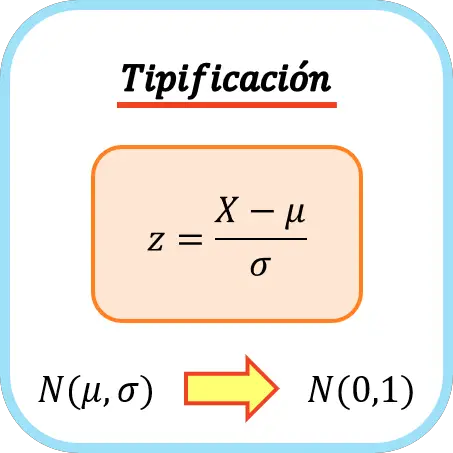
In de statistiek is normalisatie een proces waarbij een lineaire transformatie wordt toegepast op een verdeling, zodat het gemiddelde en de standaarddeviatie respectievelijk gelijk zijn aan nul en één.

Preciezer gezegd, bij typen wordt het gemiddelde van de willekeurige variabele afgetrokken en vervolgens gedeeld door de standaarddeviatie.

Typen kan ook normalisatie of standaardisatie worden genoemd.

Invoerformule

Om een variabele te classificeren, moet u het gemiddelde ervan aftrekken en deze vervolgens delen door de standaarddeviatie. De formule voor het invoeren van een variabele is daarom als volgt:

Goud

$\mu$

is het gemiddelde van de variabele

$X$

$\sigma$

de standaardafwijking (of standaardafwijking).

Daarom is de invoer feitelijk een variabeleverandering, aangezien er een lineaire transformatie op de variabele wordt toegepast.

Voorbeeld invoer

Gezien de definitie van typificatie en de formule ervan, vindt u hieronder een concreet voorbeeld om het concept volledig te begrijpen.

Een continue willekeurige variabele volgt een normale verdeling met een gemiddelde van 45 en een standaarddeviatie van 10. Wat is de kans op het verkrijgen van een waarde kleiner dan of gelijk aan 60?

$N(45,10)$

Om de waarschijnlijkheid van een normale verdeling te vinden, moeten we de karakteristieke tabel gebruiken, maar om dit te doen moeten we eerst het typeproces uitvoeren. Dus trekken we het gemiddelde af en delen we door de standaardafwijking tot de waarschijnlijkheidswaarde:

$\displaystyle P(X\leq 60)=P\left(Z\leq\frac{60-45}{10}\right)=P(Z\leq 1,5)$

Zodra we gestandaardiseerd hebben, gaan we verder met de normale verdelingswaarschijnlijkheidstabel om te zien met welke waarschijnlijkheid de waarde van 1,5 overeenkomt:

Zoals te zien is in de typeringstabel van de normale verdeling, komt de in de vorige stap berekende waarde overeen met de volgende waarschijnlijkheid:

$\displaystyle P(Z\leq 1,5)=0,9332$

De kans op het verkrijgen van een waarde gelijk aan of kleiner dan 60 is daarom 93,32%.

Typeoefening opgelost

Bereken de volgende kansen van een normale verdeling waarvan het gemiddelde en de standaarddeviatie respectievelijk 120 en 50 zijn.

$N(120,50)$

De kans op het verkrijgen van een waarde kleiner dan of gelijk aan 208.
De kans op het verkrijgen van een waarde groter dan 137.

Zie de oplossing

In beide delen van het probleem moeten we de normale verdeling invoeren om de kansen te berekenen.

We beginnen met het berekenen van de waarschijnlijkheidstypering van een waarde kleiner dan of gelijk aan 208:

$\displaystyle P(X\leq 208)=P\left(Z\leq\frac{208-120}{50}\right)=P(Z\leq 1,76)$

En laten we nu naar de bovenstaande tabel kijken met welke waarschijnlijkheid de waarde 1,76 overeenkomt:

$\displaystyle P(Z\leq 1,76)=0,9608$

Ten tweede berekenen we de kans op het verkrijgen van een waarde groter dan 137. Op dezelfde manier beginnen we met het typen van de variabele:

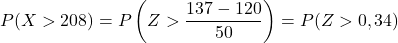$\displaystyle P(X> 208)=P\left(Z>\frac{137-120}{50}\right)=P(Z>0,34)“ title=“Rendered by QuickLaTeX.com“ height=“43″ width=“398″ style=“vertical-align: -17px;“> <p class=$ De bijgevoegde tabel heeft echter alleen de laagste cumulatieve kansen, dus om de tabel te gebruiken moeten we eerst de waarschijnlijkheid transformeren:

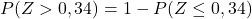$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)“ title=“Rendered by QuickLaTeX.com“ height=“19″ width=“252″ style=“vertical-align: -5px;“> <p class=$ En ten slotte zullen we uit de bijgevoegde tabel de waarschijnlijkheid opmerken die overeenkomt met de berekende waarde van Z:

$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)=1-0,6331=0,3669″ title=“Rendered by QuickLaTeX.com“ height=“19″ width=“435″ style=“vertical-align: -5px;“> <div class=$

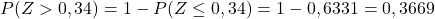
Wat is het nut van typen?

Om de betekenis van typificatie te begrijpen, zullen we zien waarvoor het wordt gebruikt en wanneer een variabele moet worden getypt.

Standaardisatie wordt voornamelijk gebruikt om de waarden van distributies met verschillende gemiddelden en varianties te vergelijken. Op dezelfde manier wordt standaardisatie ook gebruikt om een waarschijnlijkheid te berekenen.

Door twee waarden van verdelingen met verschillende kenmerken te standaardiseren, kunnen we zien welke waarde groter of kleiner is ten opzichte van de gehele verdeling. Met andere woorden: door het typeringsproces toe te passen, kunnen we zien welke waarde het dichtst of het verst verwijderd is van het gemiddelde van de verdeling ervan.

Bovendien maakt typering, zoals hierboven uitgelegd, ook de berekening van kansen mogelijk, aangezien waarschijnlijkheidstabellen over het algemeen gebaseerd zijn op een getypeerde verdeling.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder