One-way of two-way anova: wanneer gebruik je ze?
Een ANOVA , een afkorting van „Analysis of Variance“, wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.
De twee meest voorkomende typen ANOVA zijn eenrichtings-ANOVA en tweerichtings-ANOVA.
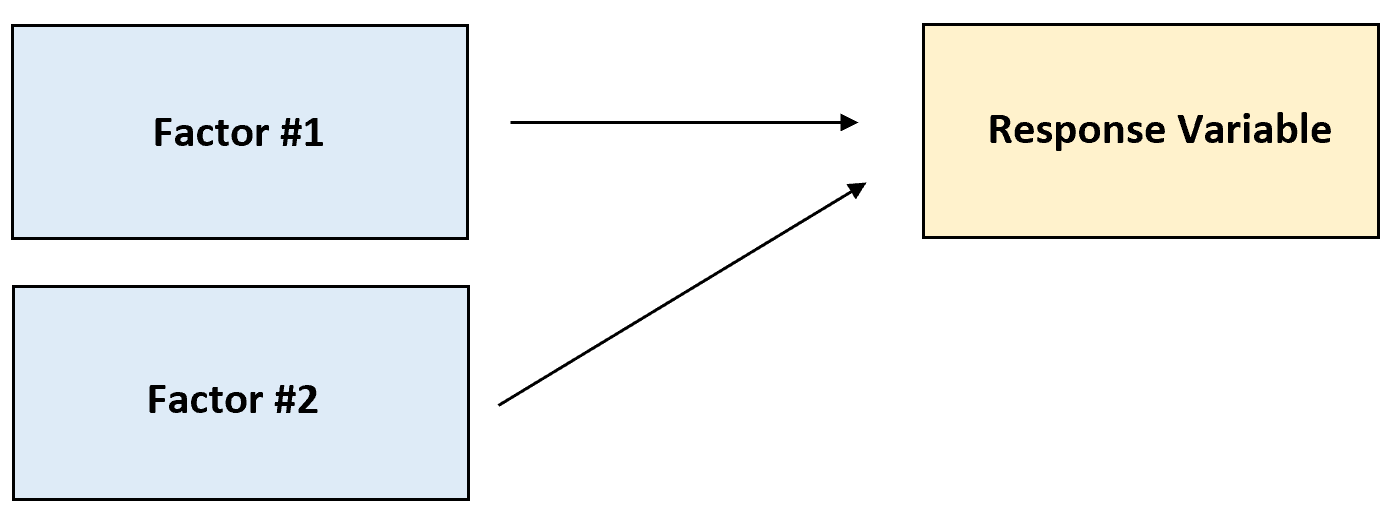
One-way ANOVA: wordt gebruikt om te bepalen hoe een factor een responsvariabele beïnvloedt.
Tweerichtings-ANOVA: wordt gebruikt om te bepalen hoe twee factoren een responsvariabele beïnvloeden en om te bepalen of er al dan niet een interactie is tussen de twee factoren op de responsvariabele.
De volgende voorbeelden geven een voorbeeld van hoe u elk type ANOVA kunt uitvoeren.
Voorbeeld: One-way ANOVA
Stel dat een hoogleraar wil weten of drie verschillende studietechnieken tot verschillende toetsscores leiden. Om dit te testen rekruteert hij dertig studenten om deel te nemen aan een onderzoek en vraagt hij elke student willekeurig een van de drie technieken te gebruiken ter voorbereiding op een examen. Na een maand maken alle studenten dezelfde toets.
De testresultaten van elke student worden hieronder weergegeven:
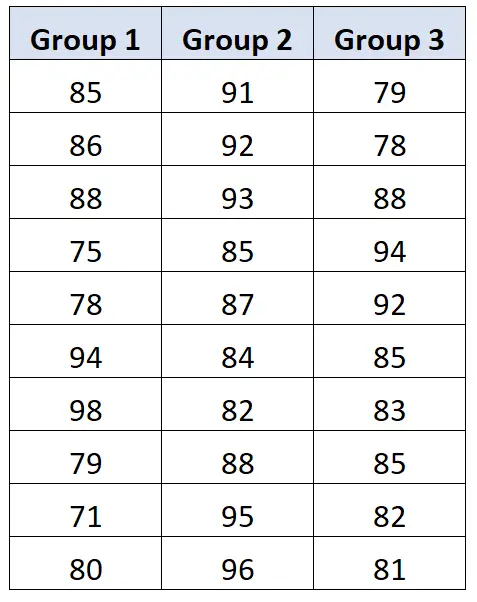
De professor voert een one-way ANOVA uit en bekomt de volgende resultaten:
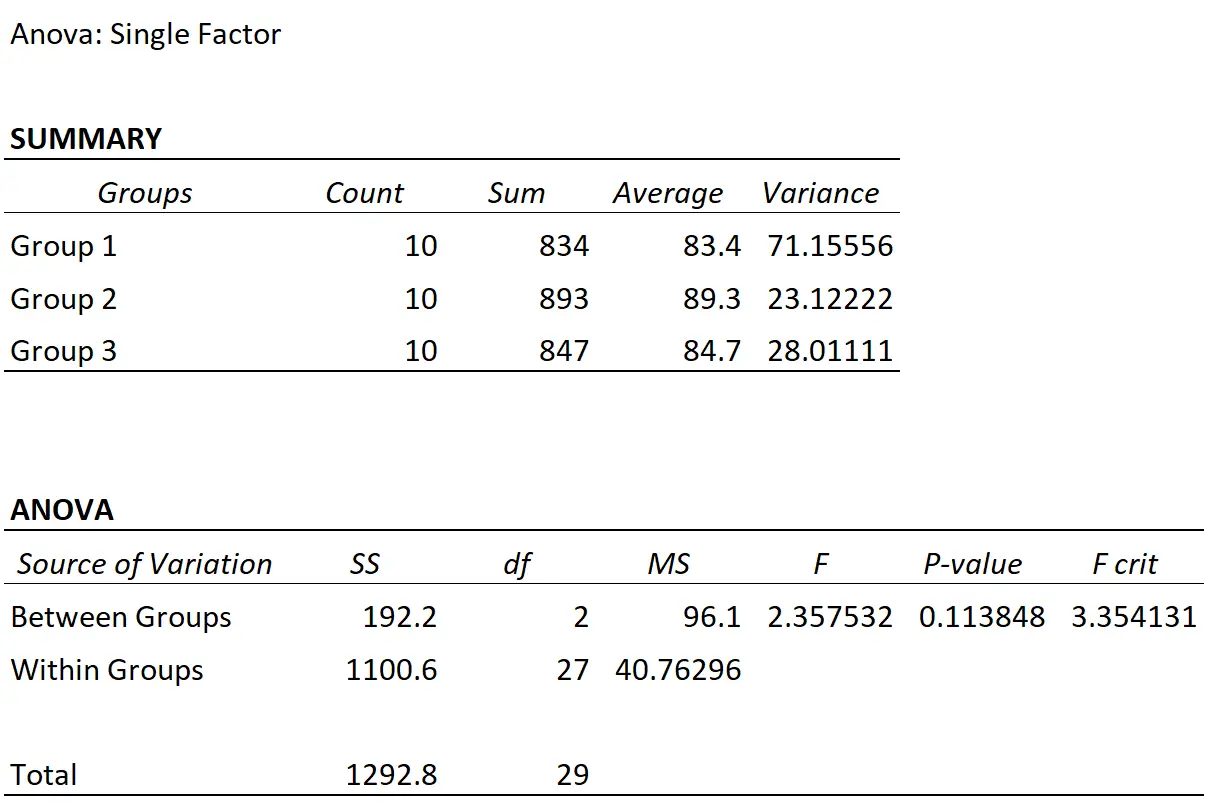
De F-teststatistiek is 2,3575 en de overeenkomstige p-waarde is 0,1138 . Omdat deze p-waarde niet kleiner is dan 0,05, hebben we onvoldoende bewijs om te zeggen dat de drie studietechnieken tot verschillende gemiddelde examenscores leiden.
Voorbeeld: tweeweg-ANOVA
Stel dat een botanicus wil weten of de plantengroei wordt beïnvloed door blootstelling aan zonlicht en de frequentie van water geven. Ze plant 40 zaden en laat ze twee maanden lang groeien onder verschillende omstandigheden wat betreft blootstelling aan de zon en waterfrequentie. Na twee maanden registreert ze de hoogte van elke plant. De resultaten worden hieronder weergegeven:
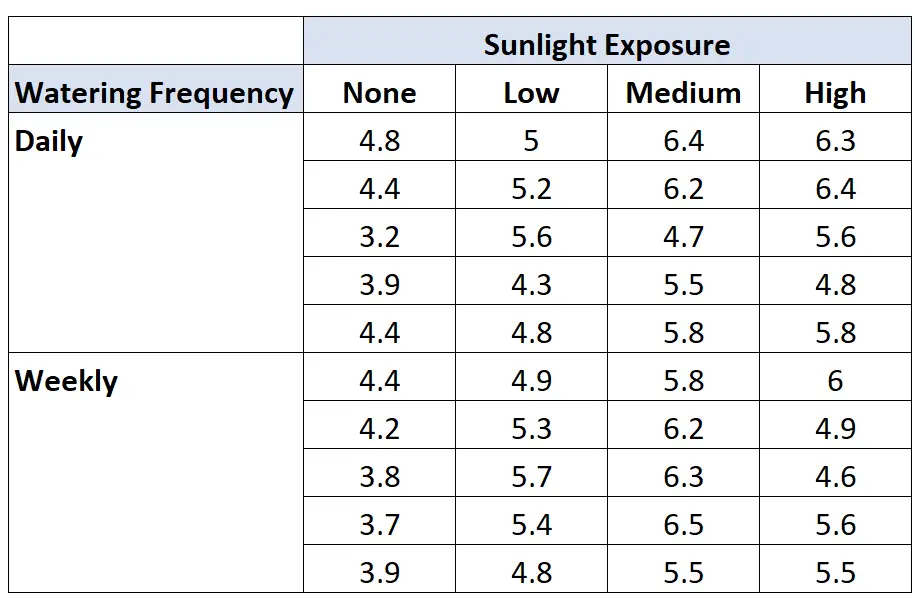
De professor voert een tweezijdige ANOVA uit en bekomt de volgende resultaten:
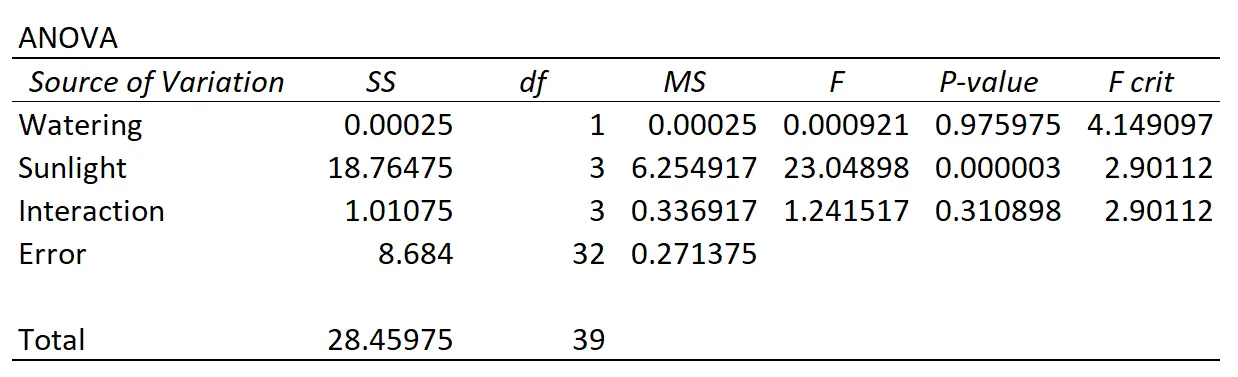
Zo interpreteert u de resultaten:
- De p-waarde voor de interactie tussen de waterfrequentie en de blootstelling aan de zon was 0,310898 . Dit is niet statistisch significant op het alfaniveau van 0,05.
- De p-waarde voor de bewateringsfrequentie was 0,975975 . Dit is niet statistisch significant op het alfaniveau van 0,05.
- De p-waarde voor blootstelling aan de zon was 0,000003 . Dit is statistisch significant op het alfaniveau van 0,05.
Deze resultaten geven aan dat blootstelling aan de zon de enige factor is met een statistisch significant effect op de planthoogte.
En omdat er geen interactie-effect is, is het effect van blootstelling aan de zon consistent op elk niveau van de bewateringsfrequentie. Simpel gezegd: of een plant dagelijks of wekelijks water krijgt, heeft geen invloed op de invloed van blootstelling aan de zon op een plant.
Praktisch: Welke ANOVA moet je gebruiken?
Gebruik de volgende oefenproblemen om beter te begrijpen wanneer u eenrichtings- of tweerichtings-ANOVA moet gebruiken.
Probleem #1: landbouw
Een boer wil weten of drie verschillende meststoffen tot verschillende opbrengsten leiden. Om dit te testen, strooit hij elk type meststof uit op 10 verschillende velden en meet hij de totale opbrengst aan het einde van het groeiseizoen.
Welk type ANOVA moet hij gebruiken om te bepalen of verschillende meststoffen tot verschillende gewasopbrengsten leiden?
Antwoord: Hij zou een one-way ANOVA moeten gebruiken omdat hij maar naar één factor kijkt: kunstmest. Een one-way ANOVA kan hem vertellen of er al dan niet een statistisch significant verschil is in de gewasopbrengsten tussen de drie verschillende soorten kunstmest.
Probleem #2: biologie
Een bioloog wil weten hoe verschillende bodemniveaus (laag, gemiddeld, hoog) en waterfrequenties (wekelijks, maandelijks) de groei van een bepaalde plant beïnvloeden.
Welk type ANOVA moet worden gebruikt om te bepalen of verschillende combinaties van blootstelling aan de zon en de waterfrequentie tot verschillende niveaus van plantengroei leiden?
Antwoord: Ze moet een tweerichtings-ANOVA gebruiken omdat ze naar twee factoren kijkt: blootstelling aan zonlicht en de frequentie van water geven. Een tweerichtings-ANOVA kan uitwijzen of verschillende niveaus van elke factor de plantengroei verschillend beïnvloeden en of er al dan niet een interactie-effect is tussen zonlicht en de waterfrequentie op de plantengroei.
Probleem #3: Medicijnen
Een medisch onderzoeker wil weten of vier verschillende medicijnen verschillende gemiddelde verlagingen van de bloeddruk bij patiënten veroorzaken. Het wijst willekeurig 20 patiënten toe om elk medicijn een maand lang te gebruiken, en meet vervolgens de verlaging van de bloeddruk bij elke patiënt.
Welk type ANOVA moet worden gebruikt om te bepalen of de vier verschillende geneesmiddelen verschillende effecten hebben op het verlagen van de bloeddruk?
Antwoord: Hij zou een one-way ANOVA moeten gebruiken omdat hij maar naar één factor kijkt: het type medicijn. Een one-way ANOVA kan hem vertellen of er al dan niet een statistisch significant verschil is in de gemiddelde bloeddrukdaling tussen de vier soorten medicijnen.
Aanvullende bronnen
Gebruik de volgende tutorials om eenrichtings-ANOVA beter te begrijpen:
- Een inleiding tot One-Way ANOVA
- Eenrichtings-ANOVA uitvoeren in Excel
- Eenrichtings-ANOVA uitvoeren in R
En gebruik deze tutorials om tweerichtings-ANOVA beter te begrijpen:
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder