Een inleiding tot uniforme distributie

De uniforme verdeling is een kansverdeling waarbij elke waarde tussen een interval van a tot en met b dezelfde kans heeft om te voorkomen.

Als een willekeurige variabele X een uniforme verdeling volgt, kan de kans dat X een waarde tussen x ₁ en x ₂ aanneemt, worden gevonden met de volgende formule:

P(x ₁ < X < x ₂ ) = (x ₂ – x ₁ ) / (b – a)

Goud:

• x ₁ : de lagere rentewaarde
• x ₂ : de hoogste rentewaarde
• a: de minimaal mogelijke waarde
• b: de maximaal mogelijke waarde

Stel bijvoorbeeld dat het gewicht van de dolfijnen gelijkmatig verdeeld is tussen de 100 en 150 pond.

Als we willekeurig een dolfijn selecteren, kunnen we de bovenstaande formule gebruiken om de waarschijnlijkheid te bepalen dat de gekozen dolfijn tussen de 120 en 130 pond weegt:

• P(120 < X < 130) = (130 – 120) / (150 – 100)
• P(120 < X < 130) = 10/50
• P(120 <X<130) = 0,2

De kans dat de gekozen dolfijn tussen de 120 en 130 pond weegt is 0,2 .

Visualiseer uniforme distributie

Als we een dichtheidsplot maken om de uniforme verdeling te visualiseren, zou het er als volgt uitzien:

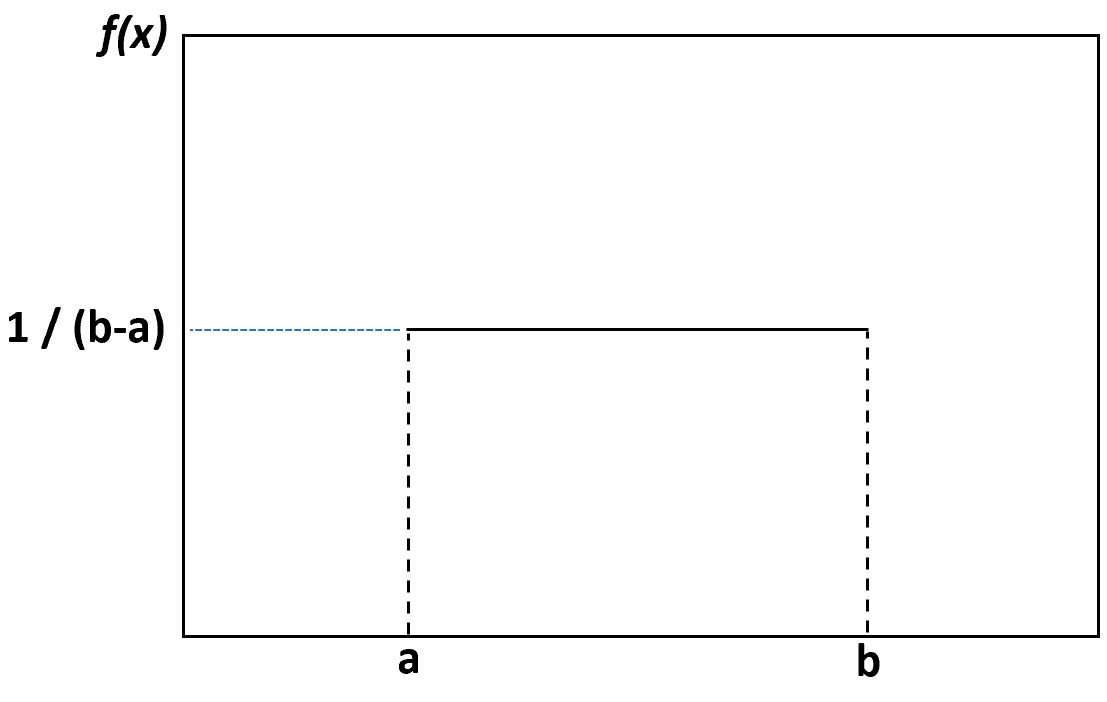
Elke waarde tussen de ondergrens a en de bovengrens b heeft dezelfde waarschijnlijkheid van voorkomen en elke waarde buiten deze grenzen heeft een waarschijnlijkheid van nul.

In ons vorige voorbeeld zeiden we bijvoorbeeld dat het gewicht van dolfijnen gelijkmatig verdeeld is tussen de 100 en 150 pond. U kunt deze verdeling als volgt visualiseren:

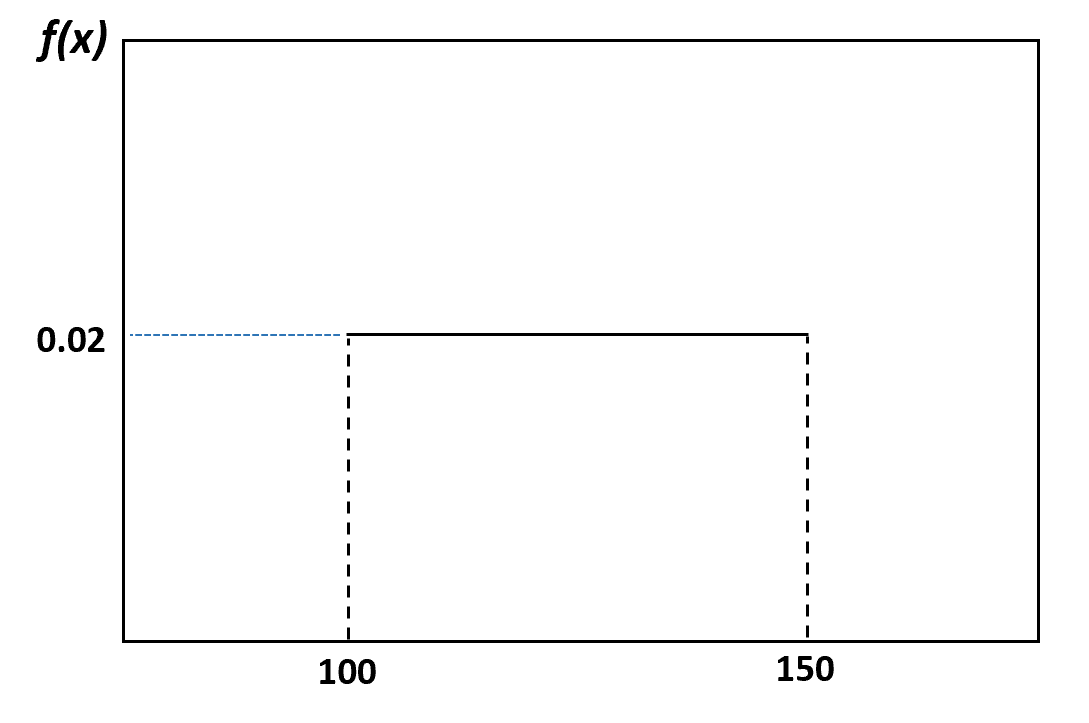
En de waarschijnlijkheid dat een willekeurig geselecteerde dolfijn tussen de 120 en 130 pond weegt, kan als volgt worden gevisualiseerd:

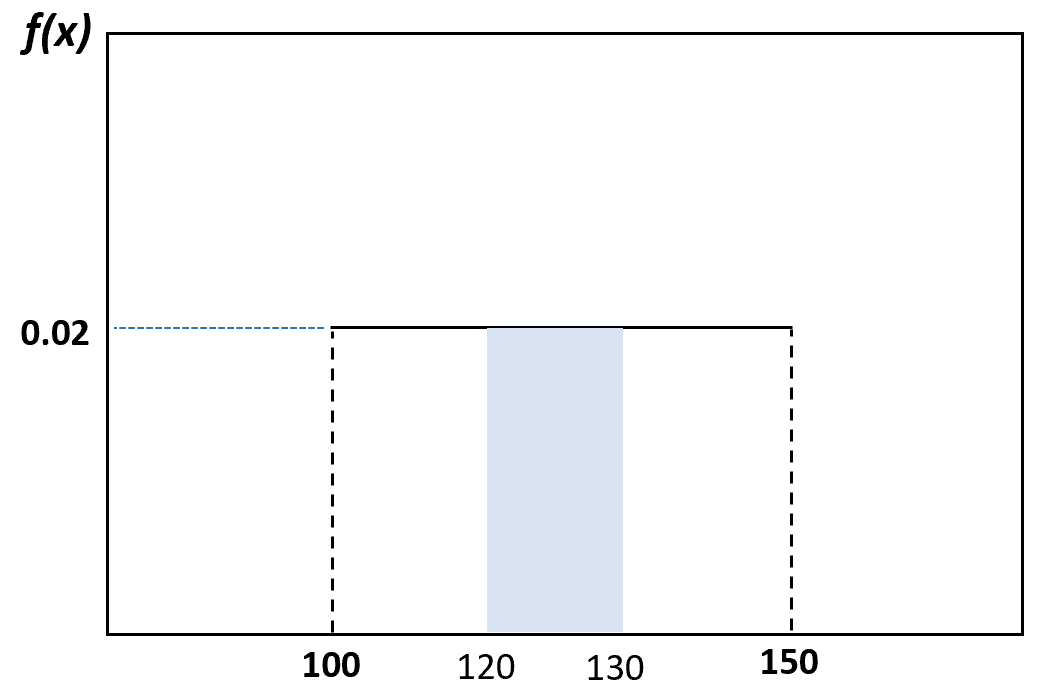
Eigenschappen van uniforme distributie

De uniforme verdeling heeft de volgende eigenschappen:

• Gemiddeld: (a + b) / 2
• Mediaan: (a + b) / 2
• Standaardafwijking: √ (b – a) ² / 12
• Verschil: (b – a) ² / 12

Stel bijvoorbeeld dat het gewicht van de dolfijnen gelijkmatig verdeeld is tussen de 100 en 150 pond.

Voor deze verdeling kunnen we de volgende eigenschappen berekenen:

• Gemiddeld gewicht: (a + b) / 2 = (150 + 100) / 2 = 125
• Mediaan gewicht: (a + b) / 2 = (150 + 100) / 2 = 125
• Standaardafwijking van gewicht: √ (150 – 100) ² / 12 = 14,43
• Gewichtsvariatie: (150 – 100) ² / 12 = 208,33

Problemen met uniforme distributiepraktijken

Gebruik de volgende oefenproblemen om uw kennis van de uniforme verdeling te testen.

Vraag 1: Elke 20 minuten komt er een bus aan bij een bushalte. Als u bij de bushalte aankomt, hoe groot is dan de kans dat de bus binnen 8 minuten of minder arriveert?

Oplossing 1: De minimale wachttijd is 0 minuten en de maximale wachttijd is 20 minuten. De onderste rentewaarde is 0 minuten en de bovenste rentewaarde is 8 minuten.

We zouden de waarschijnlijkheid dus als volgt berekenen:

P(0 < X < 8) = (8-0) / (20-0) = 8/20 = 0,4 .

Vraag 2: De duur van een NBA-wedstrijd is gelijkmatig verdeeld tussen 120 en 170 minuten. Wat is de kans dat een willekeurig gekozen NBA-wedstrijd langer dan 155 minuten duurt?

Oplossing 2: De minimale duur is 120 minuten en de maximale duur is 170 minuten. De onderste rentewaarde is 155 minuten en de bovenste rentewaarde is 170 minuten.

We zouden de waarschijnlijkheid dus als volgt berekenen:

P(155 < X < 170) = (170-155) / (170-120) = 15/50 = 0,3 .

Vraag 3: Het gewicht van een bepaalde kikkersoort is gelijkmatig verdeeld tussen de 15 en 25 gram. Als je willekeurig een kikker selecteert, hoe groot is dan de kans dat deze tussen de 17 en 19 gram weegt?

Oplossing 3: Het minimale gewicht is 15 gram en het maximale gewicht is 25 gram. De onderste rentewaarde is 17 gram en de bovenste rentewaarde is 19 gram.

We zouden de waarschijnlijkheid dus als volgt berekenen:

P(17 < X < 19) = (19-17) / (25-15) = 2/10 = 0,2 .

Opmerking: we kunnen de Uniforme Verdelingscalculator gebruiken om onze antwoorden op elk van deze problemen te controleren.