Validatieset en testset: wat is het verschil?

Wanneer we een machine learning-algoritme aan een dataset aanpassen, verdelen we de dataset doorgaans in drie delen:

1. Trainingsset : wordt gebruikt om het model te trainen.

2. Validatieset : gebruikt om modelparameters te optimaliseren.

3. Testset : gebruikt om een onbevooroordeelde schatting te verkrijgen van de uiteindelijke modelprestaties.

Het volgende diagram biedt een visuele uitleg van deze drie verschillende soorten gegevenssets:

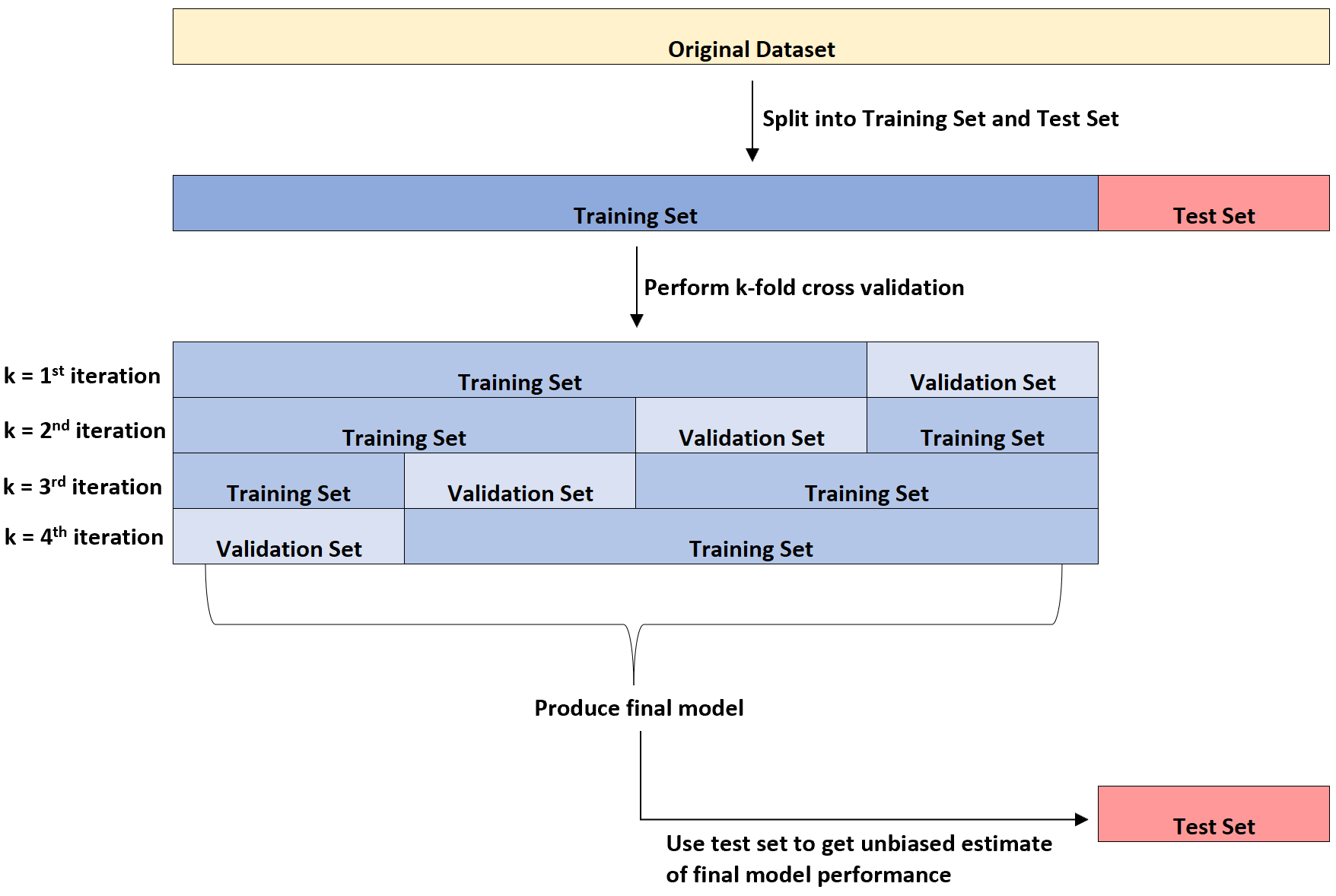
Een punt van verwarring bij studenten is het verschil tussen de validatieset en de testset.

Simpel gezegd wordt de validatieset gebruikt om de modelparameters te optimaliseren, terwijl de testset wordt gebruikt om een onbevooroordeelde schatting van het uiteindelijke model te geven.

Er kan worden aangetoond dat het foutenpercentage zoals gemeten door k-voudige kruisvalidatie de neiging heeft het werkelijke foutenpercentage te onderschatten zodra het model wordt toegepast op een onzichtbare dataset.

Daarom passen we het uiteindelijke model aan de testset aan om een onbevooroordeelde schatting te krijgen van wat het werkelijke foutenpercentage in de echte wereld zal zijn.

Het volgende voorbeeld illustreert het verschil tussen een validatieset en een testset in de praktijk.

Voorbeeld: het verschil begrijpen tussen validatieset en testset

Laten we zeggen dat een vastgoedinvesteerder (1) het aantal slaapkamers, (2) het totale aantal vierkante meter en (3) het aantal badkamers wil gebruiken om de verkoopprijs van een bepaald huis te voorspellen.

Laten we zeggen dat hij een dataset heeft met deze informatie over 10.000 huizen. Ten eerste zal het de dataset opsplitsen in een trainingsset van 8.000 huizen en een testset van 2.000 huizen:

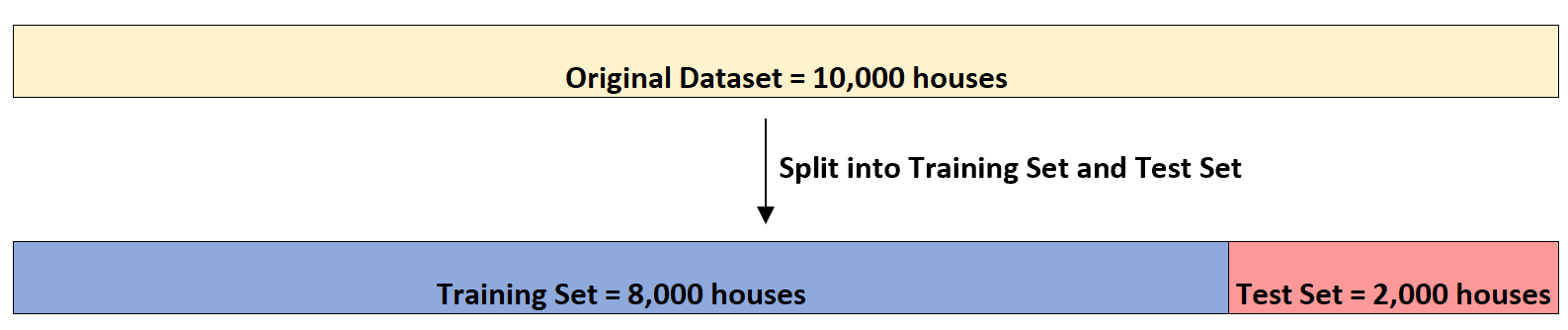
Vervolgens past het vier keer een meervoudig lineair regressiemodel aan de dataset toe. Er zullen telkens 6.000 huizen voor de trainingsset en 2.000 huizen voor de validatieset worden gebruikt.

Dit wordt k-voudige kruisvalidatie genoemd.

De trainingsset wordt gebruikt om het model te trainen en de validatieset wordt gebruikt om de prestaties van het model te evalueren. Voor de validatieset wordt telkens een andere groep van 2.000 huizen gebruikt.

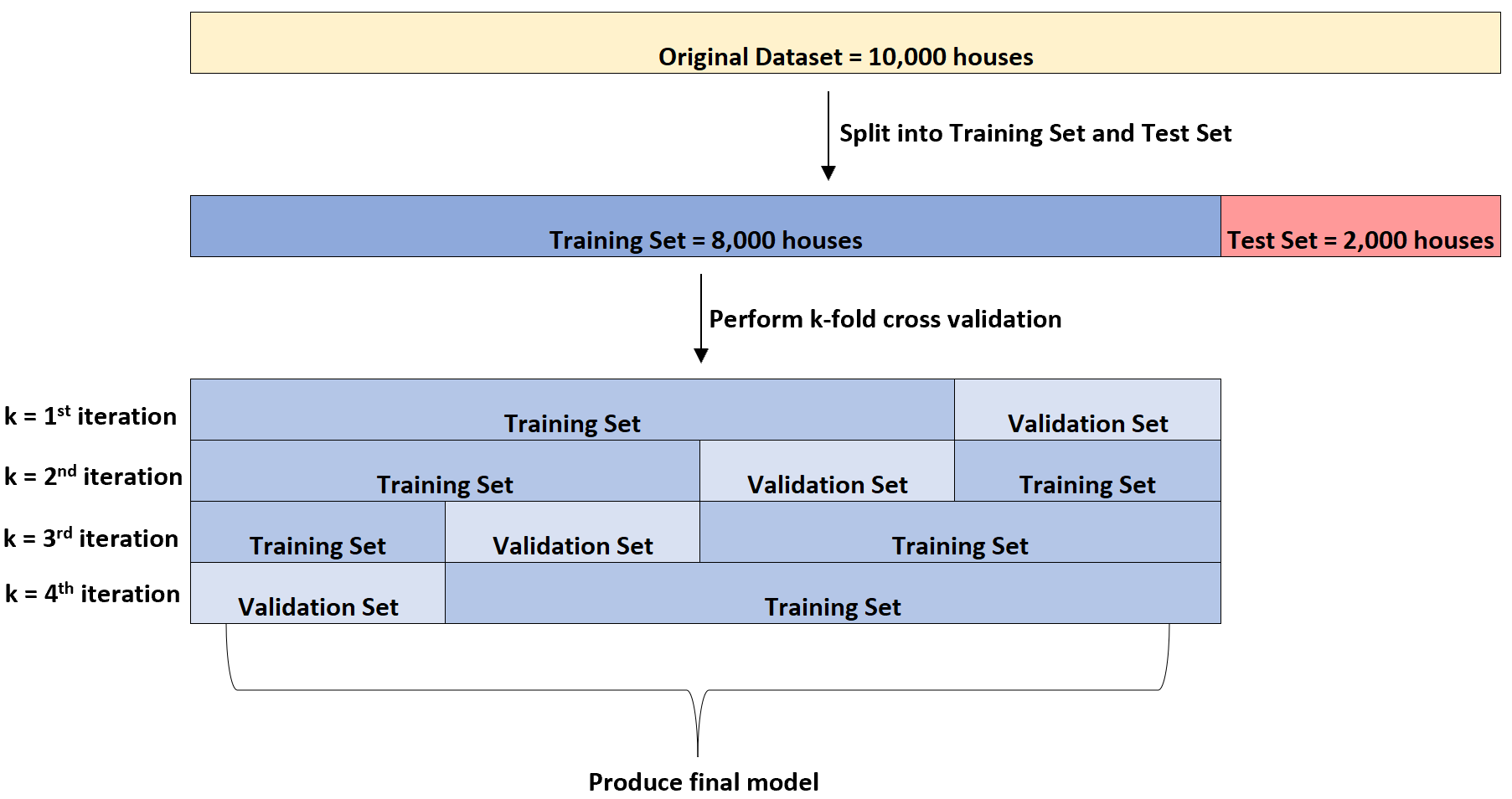
Het kan deze k-voudige kruisvalidatie uitvoeren op verschillende typen regressiemodellen om het model met de laagste fout te identificeren (dwz het model te identificeren dat het beste bij de dataset past).

Pas als het beste model is geïdentificeerd, zal het de testset met 2.000 woningen die het in het begin presenteerde, gebruiken om een onbevooroordeelde schatting te krijgen van de uiteindelijke prestaties van het model.

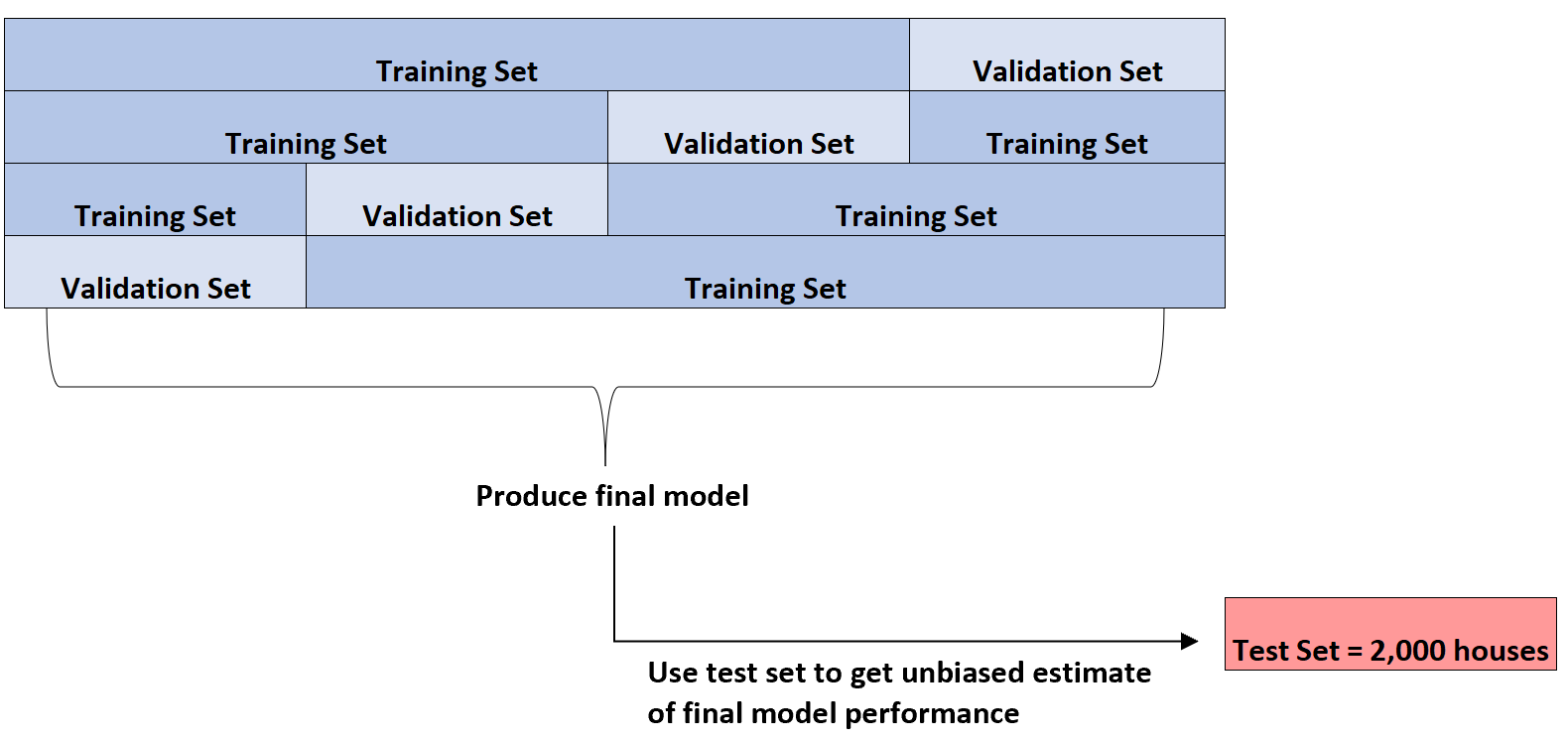
Het zou bijvoorbeeld een specifiek type regressiemodel kunnen identificeren waarvan de gemiddelde absolute fout 8.345 is. Dat wil zeggen dat het gemiddelde absolute verschil tussen de voorspelde huizenprijs en de werkelijke huizenprijs $8.345 bedraagt.

Vervolgens kan hij dit exacte regressiemodel inpassen in de testset van 2.000 huizen die nog niet zijn gebruikt en vaststellen dat de gemiddelde absolute fout van het model 8,847 bedraagt.

De onbevooroordeelde schatting van de werkelijke gemiddelde absolute fout van het model bedraagt dus $8.847.

Aanvullende bronnen

Een eenvoudige handleiding voor kruisvalidatie met K-vouwen
Hoe K-Fold kruisvalidatie uit te voeren in Python
Hoe K-Fold kruisvalidatie uit te voeren in R