Variantie

Von Dr.benjamin anderson August 5, 2023 Statistieken Keine Kommentare

In dit artikel leggen we uit wat variantie, ook wel variantie genoemd, is en hoe deze wordt berekend. U vindt er de variantieformule, een concreet voorbeeld van variantieberekening en bovendien kunt u de variantie van elke dataset berekenen met een online rekenmachine.

We laten u ook zien hoe u de variantie van gegroepeerde gegevens kunt vinden, omdat dit op een andere manier gebeurt. Ten slotte leren we u het verschil tussen populatievariantie en steekproefvariantie, het verschil tussen variantie en standaarddeviatie en de eigenschappen van deze statistische maatstaf.

Wat is variantie?

In de statistiek is variantie een maatstaf voor de spreiding die de variabiliteit van een willekeurige variabele aangeeft. De variantie is gelijk aan de som van de kwadraten van de residuen gedeeld door het totale aantal waarnemingen.

Houd er rekening mee dat het residu wordt opgevat als het verschil tussen de waarde van een statistisch gegevenspunt en het gemiddelde van de gegevensset.

In de waarschijnlijkheidstheorie is het symbool voor variantie de Griekse letter sigma kwadraat (σ ² ). Hoewel het meestal ook wordt weergegeven als Var(X) , waarbij X de willekeurige variabele is op basis waarvan de variantie wordt berekend.

Over het algemeen is het interpreteren van de variantiewaarde van een willekeurige variabele eenvoudig. Hoe groter de variantiewaarde, hoe meer verspreid de gegevens. En vice versa: hoe kleiner de variantiewaarde, hoe minder spreiding er zal zijn in de gegevensreeksen. Bij het interpreteren van de variantie moet men echter voorzichtig zijn met uitschieters , aangezien deze de variantiewaarde kunnen vertekenen.

variantie, andere maatstaven die naast spreiding worden beschouwd, zijn bereik, standaardafwijking, gemiddelde afwijking en variatiecoëfficiënt.

Hoe de kloof te berekenen

Om de variantie te berekenen, moeten de volgende stappen worden uitgevoerd:

Zoek het rekenkundig gemiddelde van de dataset.
Bereken de residuen, gedefinieerd als het verschil tussen de waarden en het gemiddelde van de dataset.
Maak elke rest vierkant.
Voeg alle resultaten toe die in de vorige stap zijn berekend.
Deel door het totale aantal gegevens. Het verkregen resultaat is de variantie van de gegevensreeks.

Concluderend is de formule voor het berekenen van de variantie van een dataset:

Goud:

$X$

is de willekeurige variabele waarvoor u de variantie wilt berekenen.
$x_i$

is de gegevenswaarde

$i$

.
$n$

is het totale aantal waarnemingen.
$\overline{X}$

is het gemiddelde van de willekeurige variabele

$X$

.

👉 U kunt de onderstaande rekenmachine gebruiken om de variantie van elke dataset te berekenen.

Om de variantie uit een gegevensreeks te extraheren, is het daarom essentieel dat u weet hoe het rekenkundig gemiddelde wordt berekend. Als u niet meer weet hoe u dit moet doen, kunt u dit bekijken in het hierboven gelinkte artikel.

Voorbeeld van afwijking

Nu we de definitie van variantie kennen, gaan we stap voor stap een oefening oplossen, zodat je kunt zien hoe de variantie van een gegevensreeks wordt verkregen.

Van een multinational is het economische resultaat bekend dat het de afgelopen vijf jaar heeft behaald; het merendeel behaalde winst, maar een jaar lang presenteerde het aanzienlijke verliezen: 11,5, 2, -9, 7 miljoen euro. Bereken de variantie van deze dataset.

Zoals we in de bovenstaande uitleg hebben gezien, is het eerste dat we moeten doen om de variantie van een gegevensreeks te vinden, het berekenen van het rekenkundig gemiddelde ervan:

$\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2$

En zodra we de gemiddelde waarde van de gegevens kennen, kunnen we de variantieformule gebruiken:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

We vervangen de gegevens uit de oefenverklaring in de formule:

$Var(X)=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5}$

Ten slotte hoeft u alleen nog maar de bewerkingen op te lossen om de variantie te berekenen:

$\begin{aligned}Var(X)&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5}\\[2ex]&= \cfrac{228,8}{5} \\[2ex]&=45,76 \ \text{millones de euros}^2\end{aligned}$

Merk op dat de variantie-eenheden dezelfde eenheden zijn van de statistische gegevens, maar dan in het kwadraat. Om deze reden bedraagt de variantie van deze gegevensgroep 45,76 miljoen euro ² .

Gatcalculator

Voer een statistische gegevensset in de volgende rekenmachine in om de variantie ervan te berekenen. Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.

Variantie voor gegroepeerde gegevens

Om de variantie van gegevens gegroepeerd in intervallen te berekenen , moeten de volgende stappen worden gevolgd:

Zoek het gemiddelde van de gegroepeerde gegevens.
Bereken de residuen van de gegroepeerde gegevens.
Maak elke rest vierkant.
Vermenigvuldig elk vorig resultaat met de frequentie van het interval.
Voeg de som toe van alle waarden verkregen in de vorige stap.
Deel door het totale aantal waarnemingen. Het resulterende getal is de variantie van de gegroepeerde gegevens.

Met andere woorden, de formule voor het berekenen van de variantie van gegevens gegroepeerd in intervallen is als volgt:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}$

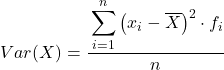
Hoewel normaal gesproken de bovenstaande formule wordt gebruikt, kan de onderstaande algebraïsche uitdrukking ook worden gebruikt omdat deze equivalent is:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{n}-\overline{X}^2$

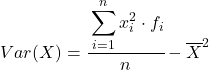
Als voorbeeld vinden we de variantie van de volgende gegroepeerde gegevensreeksen:

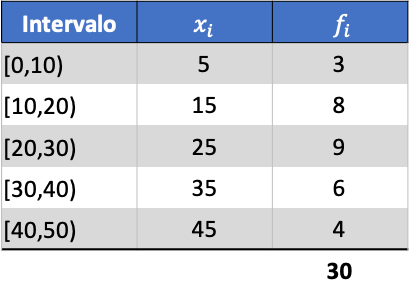
Eerst moeten we het gemiddelde van de gegroepeerde gegevens bepalen. Hiervoor voegen we in de frequentietabel een kolom toe met het product van het klassemerk en de frequentie:

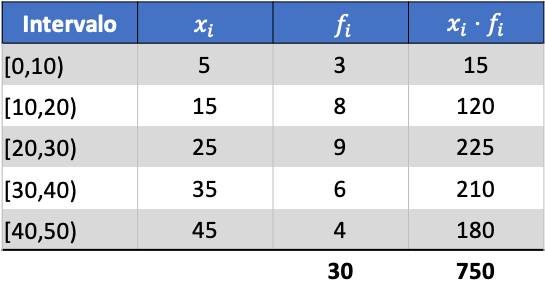
We berekenen nu het gemiddelde van de gegroepeerde gegevens door de som van de toegevoegde kolom te delen door het totale aantal gegevens:

$\overline{X}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{n}=\cfrac{750}{30}=25$

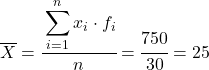
En uit het gemiddelde van de berekende gegevens kunnen we de volgende drie kolommen toevoegen:

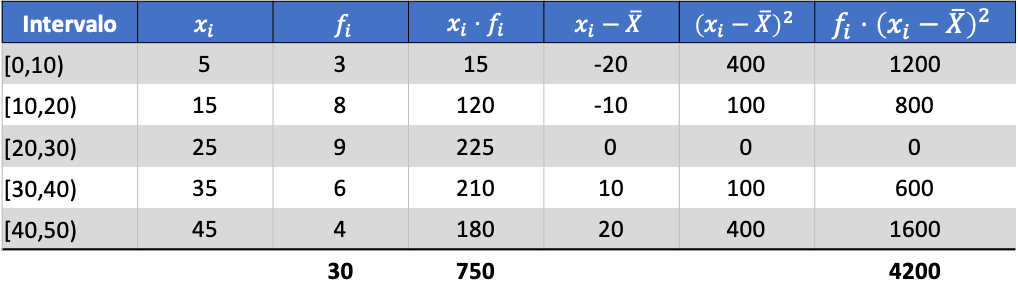
De variantie van de gepoolde dataset is dus de som van de laatste kolom gedeeld door het totale aantal waargenomen gegevens:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}=\cfrac{4200}{30}=140$

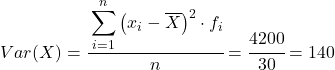
Variantie en standaarddeviatie

Variantie en standaarddeviatie (of standaarddeviatie) zijn twee spreidingsmaatstaven en geven daarom beide de mate van spreiding van de dataset aan. Het verschil tussen variantie en standaarddeviatie is echter dat de variantie over het algemeen grotere waarden heeft, omdat deze het kwadraat is van de standaarddeviatie.

De standaarddeviatie wordt doorgaans weergegeven door de Griekse letter sigma (σ), en om deze reden wordt de variantie weergegeven door de letter sigma kwadraat (σ ² ), aangezien dit de wiskundige relatie is die bestaat tussen deze twee spreidingsmetrieken.

$Var(X)=\sigma^2$

Dus zodra u de variantiewaarde van een set gegevens hebt berekend, kunt u eenvoudig de standaarddeviatiewaarde van diezelfde set vinden door eenvoudigweg de vierkantswortel van de variantie te nemen.

$\sigma=\sqrt{\sigma^2}$

Populatievariantie en steekproefvariantie

Logischerwijs verwijst populatievariantie naar de berekening van de variantie van een statistische populatie, en in plaats daarvan wordt steekproefvariantie toegepast op de berekening van de variantie van een steekproef. Dit zijn echter twee verschillende concepten, aangezien de formule voor de populatievariantie verschilt van de formule voor de steekproefvariantie.

Normaal gesproken moeten we bij variantie-oefeningen, als ze ons niets anders vertellen, om de variantie van de verstrekte dataset te vinden, de formule voor populatievariantie gebruiken, die we aan het begin van het artikel hebben uitgelegd:

$\sigma^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

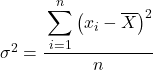
Maar misschien wordt u bij sommige problemen gevraagd om statistische gegevens als een steekproef te behandelen, in welk geval we de formule voor de steekproefvariantie moeten gebruiken:

$s^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}$

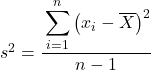
Merk op dat om aan te geven dat er een populatievariantie wordt berekend, deze wordt aangegeven met de Griekse letter σ, maar wanneer een steekproefvariantie wordt berekend, wordt de letter s gebruikt.

Zoals u kunt zien, is het enige verschil tussen de twee formules dat we de variantie van een steekproef moeten delen door het totale aantal waarnemingen minus 1. Als er in totaal bijvoorbeeld 30 gegevensitems zijn, delen we deze door 29. Maar de berekening van de teller gebeurt op precies dezelfde manier.

Variantie-eigenschappen

De variantie heeft de volgende eigenschappen:

De variantie van elke willekeurige variabele zal altijd groter dan of gelijk aan nul zijn. Als de variantie nul is, betekent dit dat alle statistische gegevens hetzelfde zijn.

$Var(x)\ge 0$

Het is duidelijk dat de variantie van een enkele waarde nul is.

$Var(a)=0\qquad a\in \mathbb{R}$

De variantie van het product van een scalair door een variabele is gelijk aan dat scalaire kwadraat maal de variantie van de variabele.

$Var(aX)=a^2\cdot Var(X)\qquad a\in \mathbb{R}$

De variantie van de som van twee afhankelijke variabelen is gelijk aan de som van de variantie van elke variabele afzonderlijk plus tweemaal de covariantie tussen de twee variabelen.

$Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)$

Als de twee variabelen dus onafhankelijk zijn, volstaat het om de varianties van hun som op te tellen om de variantie van hun som te bepalen:

$Var(X+Y)=Var(X)+Var(Y)$

De afwijking kan ook worden gedefinieerd met de wiskundige verwachting met behulp van de volgende formule:

$Var(X)=E\bigl[(X-\overline{X})^2\bigr]$

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder