Hoe u de variatiecoëfficiënt op een ti-84-rekenmachine kunt vinden

Een variatiecoëfficiënt , vaak afgekort tot CV , is een manier om de spreiding van waarden in een dataset ten opzichte van het gemiddelde te meten. Het wordt als volgt berekend:

CV = σ / μ

Goud:

• σ: de standaardafwijking van de dataset
• μ: het gemiddelde van de dataset

Simpel gezegd is de variatiecoëfficiënt de verhouding tussen de standaarddeviatie en het gemiddelde.

Het wordt vaak gebruikt om de variatie tussen twee verschillende datasets te vergelijken. In de financiële sector wordt het bijvoorbeeld gebruikt om het gemiddelde verwachte rendement van een investering te vergelijken met de verwachte standaardafwijking van de investering.

Stel dat een belegger overweegt te beleggen in de volgende twee beleggingsfondsen:

Beleggingsfonds A: gemiddelde = 9%, standaardafwijking = 12,4%

UCITS B: gemiddelde = 5%, standaardafwijking = 8,2%

De belegger kan voor elk fonds de variatiecoëfficiënt berekenen:

• CV voor beleggingsfonds A = 12,4% / 9% = 1,38
• CV voor beleggingsfonds B = 8,2% / 5% = 1,64

Omdat beleggingsfonds A een lagere variatiecoëfficiënt heeft, biedt het een beter gemiddeld rendement in vergelijking met de standaardafwijking.

Het volgende stapsgewijze voorbeeld laat zien hoe u de variatiecoëfficiënt voor de volgende gegevensset op een TI-84-rekenmachine kunt berekenen:

Gegevensset: 3, 8, 8, 13, 16, 11

Stap 1: Voer de gegevens in

Eerst zullen we de gegevenswaarden invoeren.

Druk op Stat en vervolgens op BEWERKEN . Voer vervolgens de datasetwaarden in kolom L1 in:

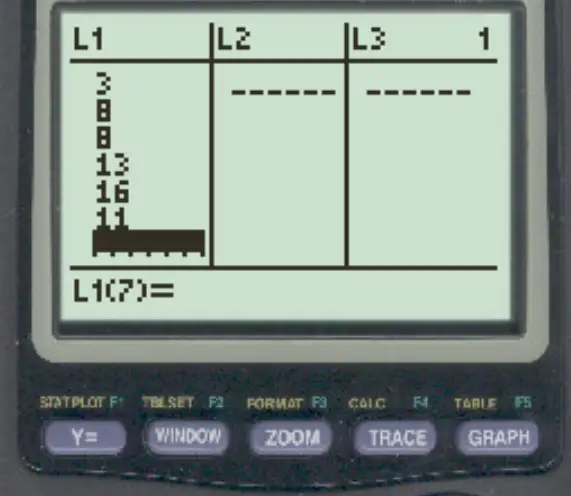
Stap 2: Zoek de variatiecoëfficiënt

Tik vervolgens op Stat , scroll naar rechts en tik op CALC .

Tik vervolgens op 1-Var-statistieken .

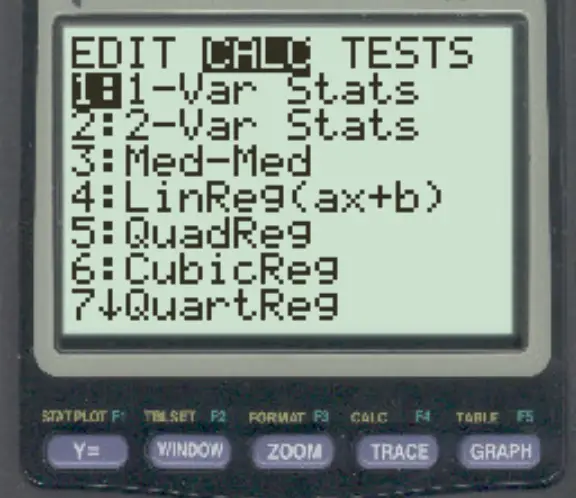
In het nieuwe scherm dat verschijnt, drukt u op Enter .

Zodra u op Enter drukt, verschijnt er een lijst met samenvattende statistieken:

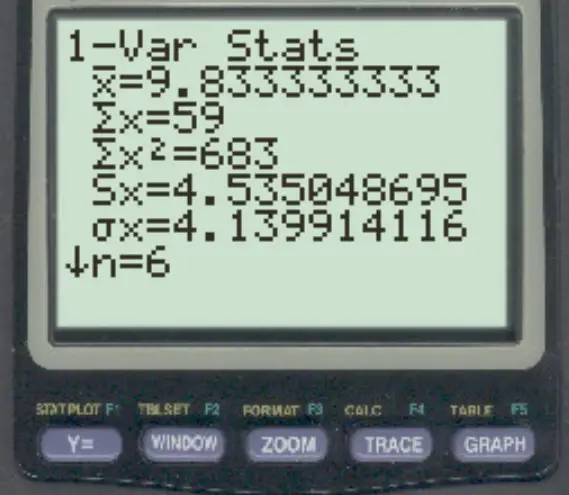
Vanuit dit scherm kunnen we de waarden van het steekproefgemiddelde en de standaarddeviatie bekijken:

• Gemiddeld ( x ): 9,8333
• Standaardafwijking van het monster (Sx): 4,535

We kunnen de variatiecoëfficiënt dan als volgt berekenen:

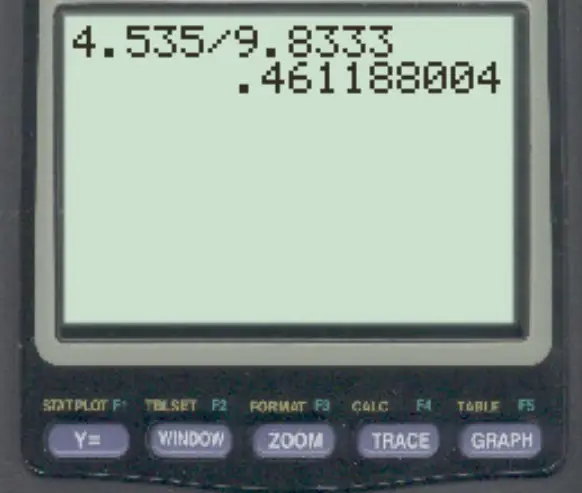
De variatiecoëfficiënt voor deze dataset blijkt 0,4611 te zijn. In procenten komt dit neer op 46,11% .

Aanvullende bronnen

Hoe u een vijfcijferige samenvatting kunt vinden op een TI-84-rekenmachine
Hoe u het interkwartielbereik kunt vinden op een TI-84-rekenmachine