Snedecor f-distributie
In dit artikel wordt uitgelegd wat de Snedecor F-distributie is en waarvoor deze wordt gebruikt. Bovendien kunt u de Snedecor F-verdelingsgrafiek zien en wat de statistische eigenschappen ervan zijn.
Wat is de Snedecor F-verdeling?
De Snedecor F-verdeling , ook wel de Fisher-Snedecor F-verdeling of eenvoudigweg F-verdeling genoemd, is een continue kansverdeling die wordt gebruikt bij statistische gevolgtrekkingen, vooral bij variantieanalyse.
Een van de eigenschappen van de Snedecor F-verdeling is dat deze wordt gedefinieerd door de waarde van twee reële parameters, m en n , die hun vrijheidsgraden aangeven. Het symbool voor de Snedecor-verdeling F is dus Fm ,n , waarbij m en n de parameters zijn die de verdeling definiëren.

![Rendered by QuickLaTeX.com \left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d407869e61ca4357ffbcb40df3bd83ab_l3.png)
De Fisher-Snedecor F-verdeling dankt zijn naam aan de Engelse statisticus Ronald Fisher en de Amerikaanse statisticus George Snedecor.
In de statistieken heeft de Fisher-Snedecor F-verdeling verschillende toepassingen. De Fisher-Snedecor F-verdeling wordt bijvoorbeeld gebruikt om verschillende lineaire regressiemodellen te vergelijken, en deze waarschijnlijkheidsverdeling wordt gebruikt bij variantieanalyse (ANOVA).
Snedecor F distributieschema
Nadat we de definitie van de Snedecor F-verdeling hebben gezien, worden hieronder de grafiek van de dichtheidsfunctie en de grafiek van de cumulatieve waarschijnlijkheid weergegeven.
In de onderstaande grafiek ziet u verschillende voorbeelden van Snedecor F-verdelingen met verschillende vrijheidsgraden.
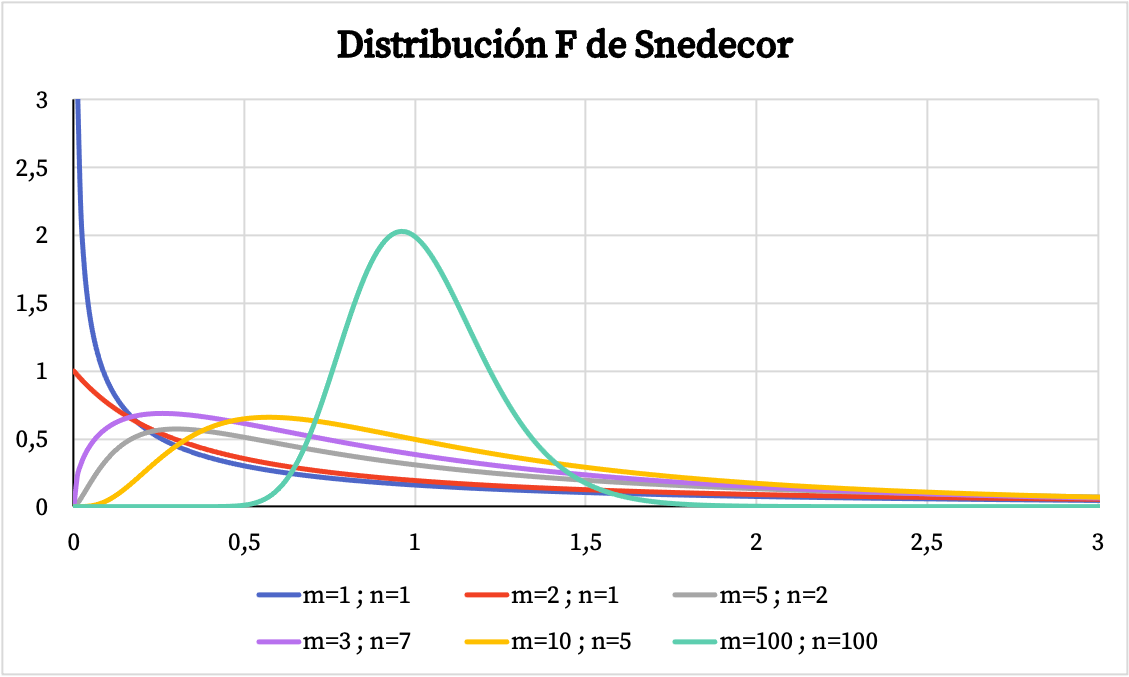
Aan de andere kant kunt u in de onderstaande grafiek zien hoe de grafiek van de cumulatieve waarschijnlijkheidsfunctie van de Snedecor F-verdeling varieert afhankelijk van de karakteristieke waarden.
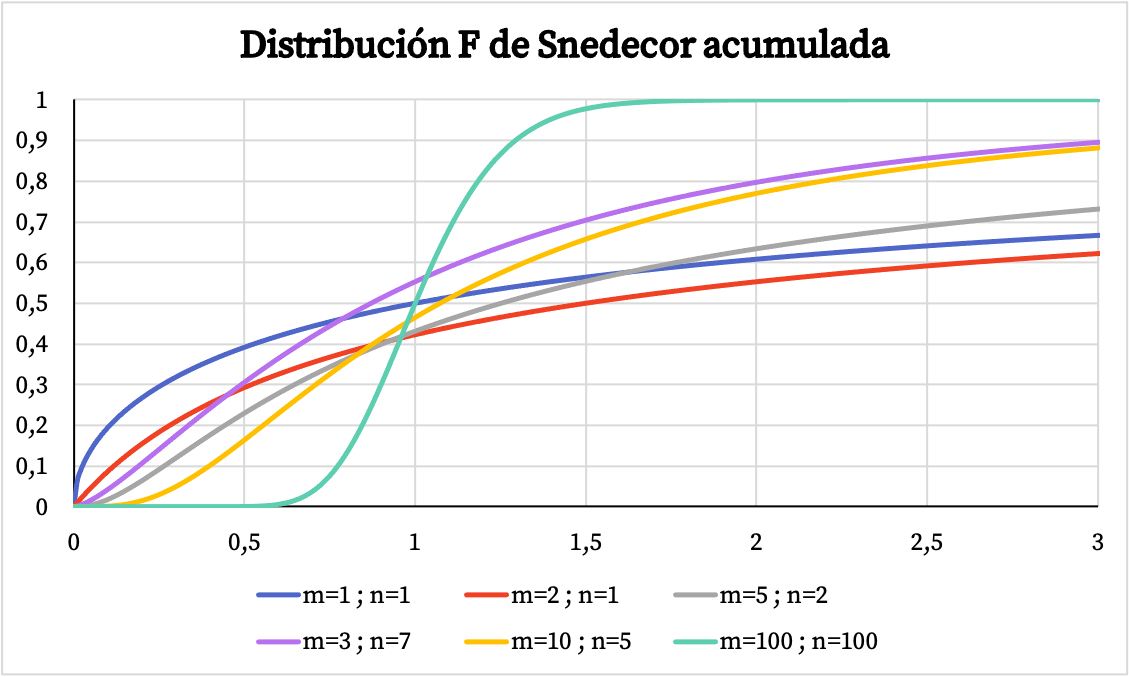
Kenmerken van de Snedecor F-verdeling
Tenslotte worden in deze sectie de belangrijkste kenmerken van de Snedecor F-distributie gepresenteerd.
- De vrijheidsgraden van de Snedecor F-verdeling, m en n , zijn twee parameters die de vorm van de verdeling definiëren. Deze karakteristieke waarden van de Snedecor F-verdeling zijn positieve gehele getallen.
![\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}“ title=“Rendered by QuickLaTeX.com“ height=“54″ width=“68″ style=“vertical-align: 0px;“></p>
</p>
<ul>
<li> Het domein van de Snedecor F-verdeling bestaat uit alle reële getallen groter dan of gelijk aan nul.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-043df156b055e7088fa83fe733825632_l3.png)
![]()
- Voor waarden van n groter dan 2 is het gemiddelde van de Snedecor F-verdeling gelijk aan n bij het aftrekken van n min 2.
![\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} “ title=“Rendered by QuickLaTeX.com“ height=“75″ width=“225″ style=“vertical-align: 0px;“></p>
</p>
<ul>
<li> Wanneer de parameter <em>n</em> groter is dan 2, kan de variantie van de Snedecor-verdeling F worden berekend door de volgende formule toe te passen:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5861b8fbc6e7aef8cac0eb21cad00c9f_l3.png)
![\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} “ title=“Rendered by QuickLaTeX.com“ height=“80″ width=“366″ style=“vertical-align: 0px;“></p>
</p>
<ul>
<li> Als de parameter <em>m</em> groter is dan 2, kan de modus van de Snedecor-verdeling F worden berekend met de volgende uitdrukking:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-9a284413da889eec7ac2e9a95e255169_l3.png)
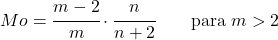
![Rendered by QuickLaTeX.com \displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-06871a7baaf462b75f545a02eac7dd11_l3.png)
- Als een variabele een Snedecor F-verdeling volgt met vrijheidsgraden m en n , dan volgt de inverse van genoemde variabele een Snedecor F-verdeling met dezelfde vrijheidsgraden, maar verandert de volgorde van zijn waarden.
![]()
- De Student-verdeling heeft de volgende relatie met de Snedecor F-verdeling:
![]()