Bemonsteringsverdeling van proporties
In dit artikel wordt uitgelegd wat de steekproefverdeling van proporties in statistieken is. Op dezelfde manier vindt u de proportie-steekproefverdelingsformule en bovendien een stap-voor-stap opgeloste oefening.
Wat is de steekproefverdeling van het aandeel?
De steekproefverdeling van proporties (of steekproefverdeling van proporties ) is de verdeling die voortvloeit uit het berekenen van het aandeel van elke mogelijke steekproef uit een populatie. Dat wil zeggen dat de steekproefverhoudingen van alle mogelijke steekproeven uit een populatie de steekproevenverdeling van die verhouding vormen.
Met andere woorden: de steekproefverdeling wordt verkregen door alle steekproeven te bestuderen die uit een populatie kunnen worden geselecteerd en door de steekproefverhouding van elke steekproef af te leiden. De reeks berekende steekproefverhoudingen vormt dus de steekproefverdeling van het aandeel.
Als u zich afvraagt waar de steekproefverdeling van het aandeel voor dient: in de statistiek wordt deze gebruikt om de waarschijnlijkheid te berekenen dat u de waarde van het populatieaandeel benadert bij het analyseren van een enkele steekproef.
Proportionele bemonsteringsverdelingsformule
Wanneer we een deel van een steekproef bestuderen, analyseren we in feite succesgevallen. Daarom volgt de willekeurige variabele in het onderzoek een binomiale waarschijnlijkheidsverdeling .
Volgens de centrale limietstelling kunnen we voor grote maten (n>30) een binomiale verdeling dichter bij een normale verdeling brengen. Daarom benadert de steekproefverdeling van het aandeel een normale verdeling met de volgende parameters:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f3408076893f390bb65baecfe38e6eff_l3.png)
Goud
![]()
is de kans op succes en
![]()
is de kans op falen
![]()
.
Opmerking: een binominale verdeling kan alleen worden benaderd als een normale verdeling als:

![]()
En
![]()
.
Omdat de steekproefverdeling van het aandeel kan worden benaderd tot een normale verdeling, is de formule voor het berekenen van elke waarschijnlijkheid die verband houdt met het aandeel van een steekproef daarom:

Goud:
-

is de steekproefaandeel.
-

is het aandeel van de bevolking.
-

is de kans op falen van de populatie,

.
-

is de steekproefomvang.
-

is een variabele gedefinieerd door de standaard normale verdeling N(0,1).
Concreet voorbeeld van verdeling van proportiemonsters
Zodra we de definitie van Proportion Sampling Distribution hebben gezien en wat de bijbehorende formules zijn, wordt hieronder een stapsgewijs opgelost voorbeeld gegeven om het concept volledig te begrijpen.
- Een industrieel bedrijf koopt batches onderdelen van een fabriek die beweert de onderdelen te produceren met slechts 3% defecte onderdelen. Om dit te controleren besluit het bedrijf een bestelling van 500 onderdelen te analyseren. Wat is de kans dat er meer dan 5% defecte onderdelen in het monster worden aangetroffen?
In dit geval is het deel van de populatie dat we willen bestuderen 0,03, dus de parameter q is equivalent aan 0,97.
![Rendered by QuickLaTeX.com \begin{array}{c}p=0,03\\[2ex]q=1-p=0,97\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f4354c268853ec7b592bcacd23f3b214_l3.png)
Om dus de waarschijnlijkheid te vinden die ze ons vragen, moeten we de overeenkomstige statistiek berekenen door de formule toe te passen die we in de vorige sectie hebben gezien:
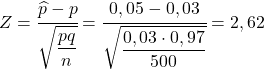
De kans op het verkrijgen van meer dan 5% defecte onderdelen is dus gelijk aan de volgende kans:
![P\left[\widehat{p}>0,05\right]=P[Z>2,62]=1-P[Z\leq 2,62]“ title=“Rendered by QuickLaTeX.com“ height=“19″ width=“360″ style=“vertical-align: -5px;“></p>
</p>
<p> Ten slotte zoeken we naar de waarschijnlijkheid van P[Z≤2,62] in de <a href=](https://statorials.org/wp-content/ql-cache/quicklatex.com-a5e5cff61f2cc97762df561b3e35a7ba_l3.png) Z-verdelingstabel en berekenen we de waarschijnlijkheid die het probleem ons vraagt:
Z-verdelingstabel en berekenen we de waarschijnlijkheid die het probleem ons vraagt:
![\begin{array}{l}P\left[\widehat{p}>0,05\right]=\\[2ex]=P[Z>2,62]=\\[2ex]=1-P[Z\leq 2,62]=\\[2ex]=1-0,9956=\\[2ex]=0,0044\end{array}“ title=“Rendered by QuickLaTeX.com“ height=“167″ width=“162″ style=“vertical-align: 0px;“></p>
</p>
<p> Concluderend is de waarschijnlijkheid dat er meer dan 5% defecte onderdelen in het geanalyseerde monster worden aangetroffen 0,44%.</p>
</div><!-- End Content -->
<!-- Start Author Box -->
<div class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-812f9b97c53e15da88b0cb7149f254c6_l3.png)
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder