Student's t-verdeling
In dit artikel wordt uitgelegd wat de Student t-verdeling is en waarvoor deze wordt gebruikt. Bovendien wordt de grafiek van Student’s t-verdeling getoond en wat de kenmerken zijn van dit type kansverdeling.
Wat is de studentenverdeling?
De Student’s t-verdeling is een kansverdeling die veel wordt gebruikt in de statistiek. Concreet wordt de Student’s t-verdeling gebruikt in de Student’s t-test om het verschil tussen de gemiddelden van twee steekproeven te bepalen en om betrouwbaarheidsintervallen vast te stellen.
De Student’s t-verdeling werd in 1908 ontwikkeld door statisticus William Sealy Gosset onder het pseudoniem „Student“.
De Student’s t-verdeling wordt gedefinieerd door het aantal vrijheidsgraden, verkregen door één eenheid af te trekken van het totale aantal waarnemingen. Daarom is de formule voor het bepalen van de vrijheidsgraden van een Student’s t-verdeling v=n-1 .
![\begin{array}{c}\nu=n-1\\[2ex]X\sim t_\nu\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-1c805dc2d6ca050feb70dad99de53402_l3.png "Rendered by QuickLaTeX.com")
Student’s t-verdelingsgrafiek
Nu we de definitie van Student’s t-verdeling kennen, gaan we kijken wat de grafiek ervan is. Hieronder kunt u dus grafisch verschillende voorbeelden zien van Student’s t-verdelingen met verschillende vrijheidsgraden.
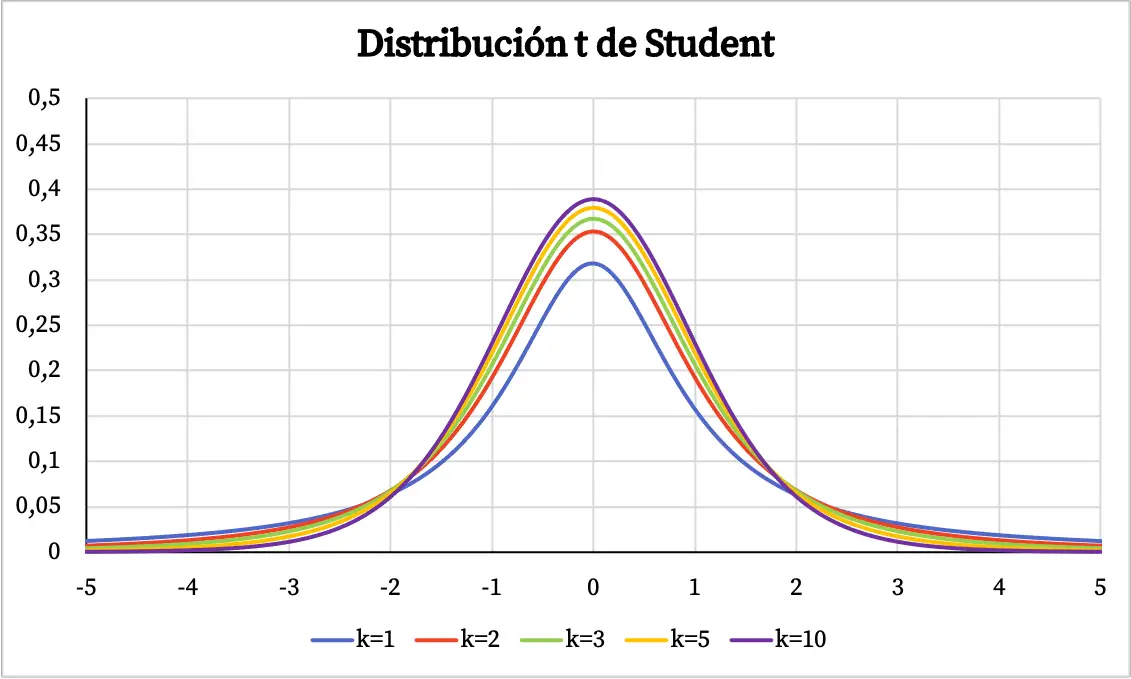
Uit de grafiek van de Student’s t-verdeling kunnen de volgende eigenschappen worden afgeleid:
- De Student t-verdeling is symmetrisch gecentreerd op 0 en heeft een belvorm.
- De Student’s t-verdeling is meer verspreid dan de normale verdeling, dat wil zeggen dat de curve van de Student’s t-verdeling breder is.
- Hoe meer vrijheidsgraden de Student’s t-verdeling heeft, hoe lager de spreiding ervan.
In de bovenstaande grafiek is de dichtheidsfunctie van de Student’s t-verdeling uitgezet tegen de vrijheidsgraden. Hieronder kunt u echter zien hoe de cumulatieve waarschijnlijkheidsfunctie van de Student’s t-verdeling varieert:
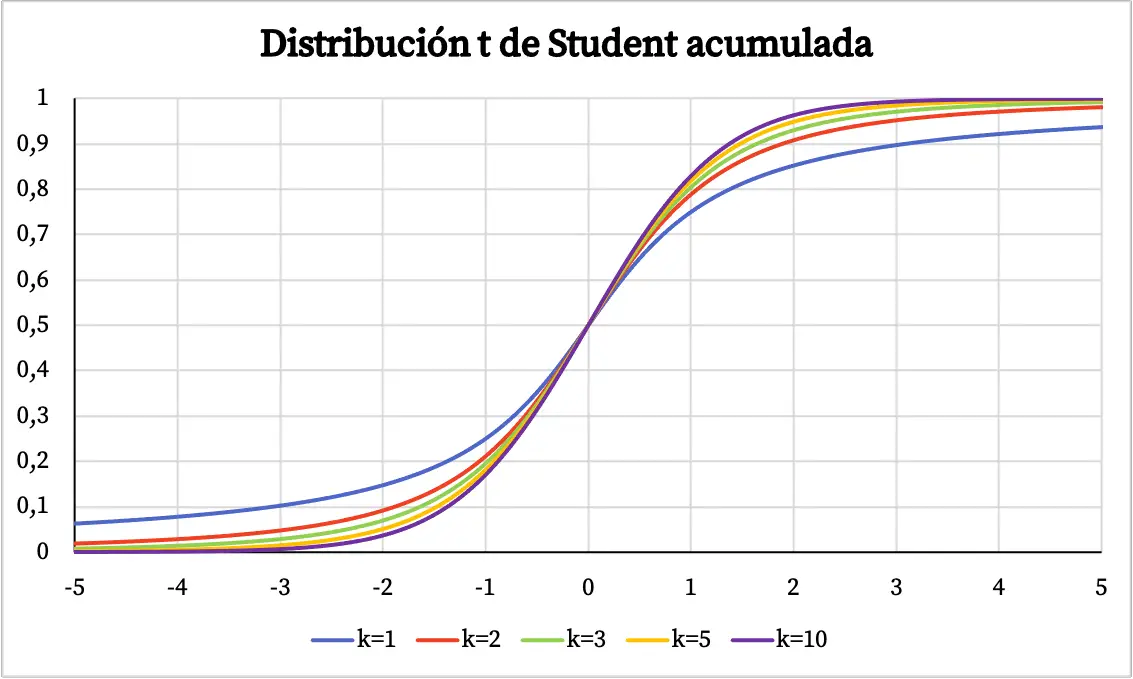
Kenmerken van de Student’s t-verdeling
De belangrijkste kenmerken van de Student’s t-verdeling worden hieronder weergegeven.
- Het domein van de Student t-verdeling bestaat uit reële getallen.
- Voor Student’s t-verdelingen met meer dan één vrijheidsgraad is het gemiddelde van de verdeling gelijk aan 0.
![\begin{array}{c}X\sim t_\nu\\[2ex] E[X]=0 \qquad \text{para }\nu>1\end{array} “ title=“Rendered by QuickLaTeX.com“ height=“55″ width=“190″ style=“vertical-align: 0px;“></p>
</p>
<ul>
<li> De variantie van een Student’s t-verdeling kan worden berekend met behulp van de volgende uitdrukking:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-d4fed5eadcaa1162752aeedb7f8a0906_l3.png)
![\begin{array}{c}X\sim t_\nu\\[2ex] Var(X)=\cfrac{\nu}{\nu-2} \qquad \text{para }\nu>2\end{array} “ title=“Rendered by QuickLaTeX.com“ height=“75″ width=“245″ style=“vertical-align: 0px;“></p>
</p>
<ul>
<li> De mediaan en modus van de Student’s t-verdeling zijn, ongeacht het aantal vrijheidsgraden, altijd 0.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-bfdcbc8a5f071a61e091b0ef6f686a16_l3.png)
![\begin{array}{c}Me=0\\[2ex]Mo=0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8d90790fce0c987648c0b30216c82214_l3.png "Rendered by QuickLaTeX.com")
- De dichtheidsfunctie van de Student t-verdeling wordt gedefinieerd door de volgende formule:
![\displaystyle P[X=x]=\frac{\Gamma((\nu+1)/2)} {\sqrt{\nu\pi}\,\Gamma(\nu/2)} (1+x^2/\nu)^{-(\nu+1)/2}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8c0f1e97a8e407e8b9e2b00ba93aee0e_l3.png "Rendered by QuickLaTeX.com")
- De cumulatieve kansverdelingsfunctie van de Student’s t-verdeling wordt gedefinieerd door de volgende formule:
![\displaystyle P[X\leq x]=\frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2};-\frac{x^2}{\nu} \right)}{\sqrt{\pi\nu}\,\Gamma \left(\frac{\nu}{2}\right)}](https://statorials.org/wp-content/ql-cache/quicklatex.com-da1e3bdf2d87c3a7dcc89c236958dcec_l3.png "Rendered by QuickLaTeX.com")
- Voor Student’s t-verdelingen met vrijheidsgraden groter dan 3 is de asymmetriecoëfficiënt nul omdat het een symmetrische verdeling is.
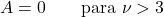
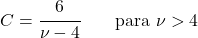Toepassingen van de Student’s t-verdeling
De Student’s t-verdeling is een kansverdeling die veel wordt gebruikt in de statistiek. Er bestaat zelfs de Student’s t-test, die wordt gebruikt om hypothesen en betrouwbaarheidsintervallen te testen.
De Student’s t-verdeling stelt ons dus in staat het verschil tussen de gemiddelden van twee steekproeven te analyseren, preciezer gezegd: het wordt gebruikt om te bepalen of twee steekproeven significant verschillende gemiddelden hebben. Op dezelfde manier wordt de Student’s t-test gebruikt om erachter te komen of de lijn verkregen uit een lineaire regressieanalyse een helling heeft of niet.
Kortom, toepassingen van de Student’s t-verdeling zijn afhankelijk van de analyse van datasets die theoretisch een normale verdeling volgen, maar het totale aantal waarnemingen is te klein om dit type verdeling te gebruiken.
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder