Vergelijking van z-scores van verschillende distributies

Een z-score vertelt u hoeveel standaarddeviaties een individuele gegevenswaarde van het gemiddelde afwijkt. Het wordt als volgt berekend:

z-score = (x – μ) / σ

Goud:

• x: individuele gegevenswaarde
• μ: populatiegemiddelde
• σ: standaarddeviatie van de populatie

Een z-score voor een individuele waarde kan als volgt worden geïnterpreteerd:

• Positieve z-score: de individuele waarde ligt boven het gemiddelde.
• Negatieve z-score: de individuele waarde is lager dan het gemiddelde.
• Een z-score van 0: de individuele waarde is gelijk aan het gemiddelde.

Z-scores zijn vooral handig als we de relatieve positie van twee gegevenspunten uit twee verschillende distributies willen vergelijken. Om dit te illustreren, bekijken we het volgende voorbeeld.

Voorbeeld: Z-scores vergelijken

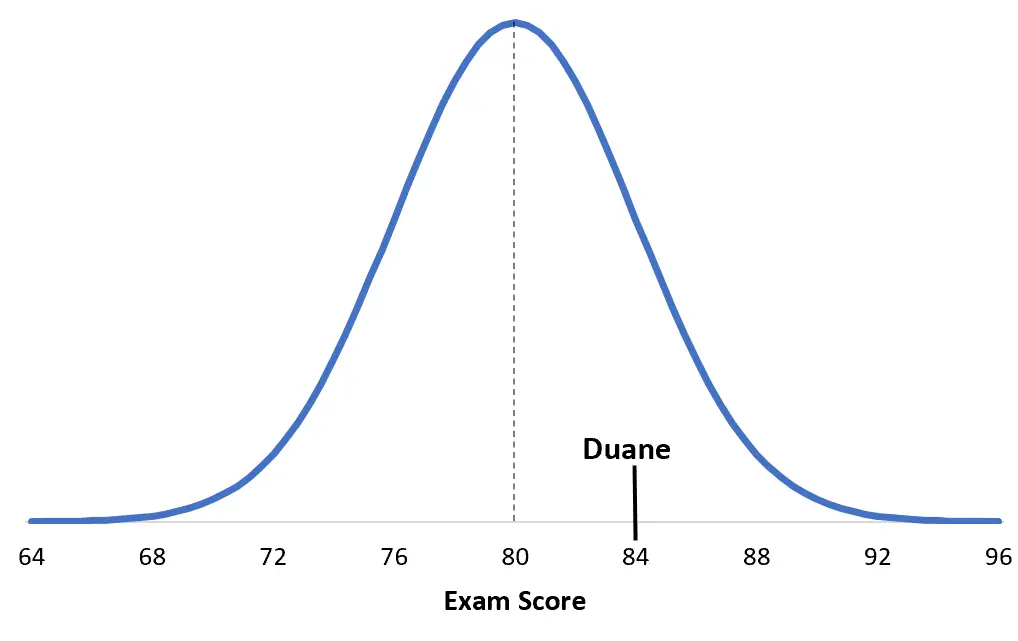
Scores op een bepaald universiteitsexamen zijn normaal verdeeld met gemiddelde μ = 80 en standaarddeviatie σ = 4. Duane scoort op dit examen een 84.

Scores op een ander universiteitsexamen worden normaal verdeeld met gemiddelde μ = 85 en standaarddeviatie σ = 8. Debbie krijgt een 90 voor dat examen.

Wie behaalde, vergeleken met hun eigen verdeling van examenscores, de beste resultaten op hun examen?

Om deze vraag te beantwoorden, kunnen we de z-score van de examenscore van elke persoon berekenen:

Duane’s z-score = (x – μ) / σ = (84 – 80) / 4 = 4 / 4 = 1

Debbie’s z-score = (x – μ) / σ = (90 – 85) / 8 = 5/8 = 0,625

Debbie Hoewel hij hoger scoorde, is de score van Duane feitelijk hoger vergeleken met de verdeling van zijn specifieke examen.

Om dit te begrijpen, helpt het om de situatie te visualiseren. Hier is de score van Duane vergeleken met zijn specifieke examenuitsplitsing:

En hier is Debbie’s score van haar examenuitsplitsing:

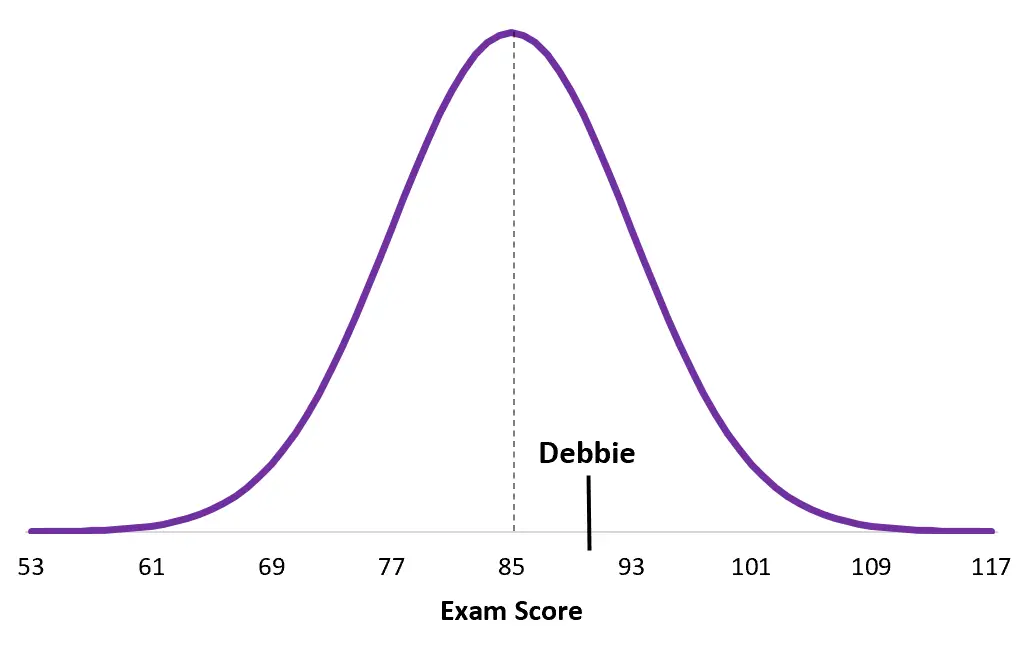
Merk op hoeveel dichter Debbie’s score bij haar populatiegemiddelde ligt dan die van Duane. Hoewel ze in totaal een hogere score heeft, is haar z-score lager, simpelweg omdat de gemiddelde score op haar specifieke examen hoger is.

Dit voorbeeld illustreert waarom z-scores zo nuttig zijn voor het vergelijken van datawaarden uit verschillende distributies: z-scores houden rekening met de gemiddelde en standaardafwijkingen van distributies, waardoor we datawaarden uit verschillende distributies kunnen vergelijken en zien welke hoger dan hun eigen uitkeringen.

Aanvullende bronnen

Z-score rekenmachine
Vergelijk Z-scorecalculator