Hoe de verwachte waarde van x^2 te berekenen

Voor een willekeurige variabele , aangeduid met X, kunt u de volgende formule gebruiken om de verwachte waarde van X ² te berekenen:

E(X ² ) = Σx ² * p(x)

Goud:

• Σ : Een symbool dat “som” betekent
• x : De waarde van de willekeurige variabele
• p(x) : De kans dat de willekeurige variabele een bepaalde waarde aanneemt

Het volgende voorbeeld laat zien hoe u deze formule in de praktijk kunt gebruiken.

Voorbeeld: Berekening van de verwachte waarde van X ²

Stel dat we de volgende kansverdelingstabel hebben die de waarschijnlijkheid beschrijft dat een willekeurige variabele,

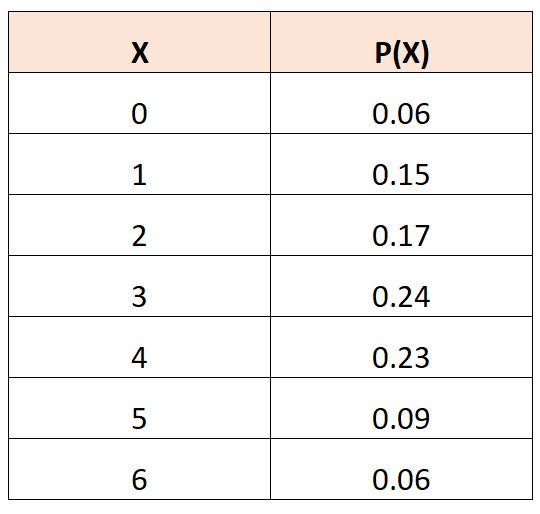
Om de verwachte waarde van X ² te berekenen, kunnen we de volgende formule gebruiken:

E(X ² ) = Σx ² * p(x)

E(X ² ) = (0) ² *.06 + (1) ² *.15 + (2) ² *.17 + (3) ² *.24 + (4) ² *.23 + (5) ² *.09 + (6) ² *.06

E( ^X2 ) = 0 + 0,15 + 0,68 + 2,16 + 3,68 + 2,25+ 2,16

E( ^X2 ) = 11,08

De verwachte waarde van ^X2 is 11,08 .

Merk op dat deze willekeurige variabele een discrete willekeurige variabele is, wat betekent dat deze slechts een eindig aantal waarden kan aannemen.

Als X een continue willekeurige variabele is, moeten we de volgende formule gebruiken om de verwachte waarde van X ² te berekenen:

E(X ² ) = ∫ x ² f(x)dx

Goud:

• ∫: Een symbool dat “integratie” betekent
• f(x) : De pdf gaat verder voor de willekeurige variabele

Bij het berekenen van de verwachte waarde van ^X2 voor een continue willekeurige variabele gebruiken we doorgaans statistische software omdat deze berekening moeilijker handmatig uit te voeren kan zijn.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in de statistiek kunt uitvoeren:

Hoe het gemiddelde van een kansverdeling te vinden
Hoe de standaarddeviatie van een kansverdeling te vinden
Hoe de variantie van een kansverdeling te vinden