Hoe de verwachte waarde van x^3 te berekenen

Voor een willekeurige variabele , aangeduid met X, kunt u de volgende formule gebruiken om de verwachte waarde van X ³ te berekenen:

E(X ³ ) = Σx ³ * p(x)

Goud:

• Σ : Een symbool dat “som” betekent
• x : De waarde van de willekeurige variabele
• p(x) : De kans dat de willekeurige variabele een bepaalde waarde aanneemt

Het volgende voorbeeld laat zien hoe u deze formule in de praktijk kunt gebruiken.

Voorbeeld: Berekening van de verwachte waarde van X ³

Stel dat we de volgende kansverdelingstabel hebben die de waarschijnlijkheid beschrijft dat een willekeurige variabele,

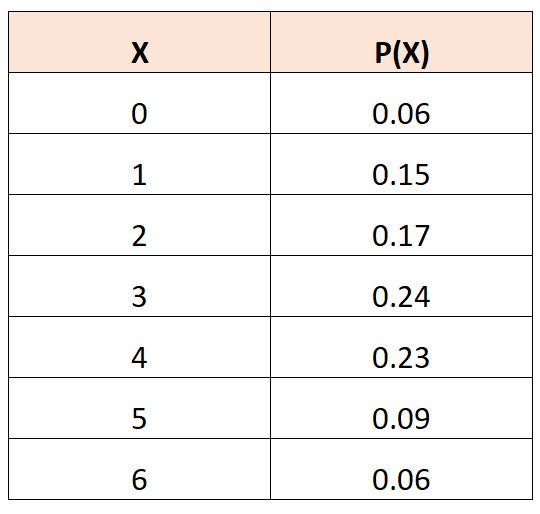
Om de verwachte waarde van X ³ te berekenen, kunnen we de volgende formule gebruiken:

E(X ³ ) = Σx ³ * p(x)

E(X ³ ) = (0) ³ *.06 + (1) ³ *.15 + (2) ³ *.17 + (3) ³ *.24 + (4) ³ *.23 + (5) ³ *.09 + (6) ³ *.06

E( ^X3 ) = 0 + 0,15 + 0,1,36 + 6,48 + 14,72 + 11,25 + 12,96

E( ^X3 ) = 45,596

De verwachte waarde van X ³ is 45.596 .

Merk op dat deze willekeurige variabele een discrete willekeurige variabele is, wat betekent dat deze slechts een eindig aantal waarden kan aannemen.

Als X een continue willekeurige variabele is, moeten we de volgende formule gebruiken om de verwachte waarde van X ³ te berekenen:

E(X ³ ) = ∫ x ³ f(x)dx

Goud:

• ∫: Een symbool dat “integratie” betekent
• f(x) : De pdf gaat verder voor de willekeurige variabele

Bij het berekenen van de verwachte waarde ^van

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in de statistiek kunt uitvoeren:

Hoe het gemiddelde van een kansverdeling te vinden
Hoe de standaarddeviatie van een kansverdeling te vinden
Hoe de variantie van een kansverdeling te vinden