Hoe u snel een regressievergelijking kunt vinden in excel

U kunt de functie LIJNSCH gebruiken om snel een regressievergelijking in Excel te vinden.

Deze functie gebruikt de volgende basissyntaxis:

 LINEST(known_y's, known_x's)

Goud:

• bekende_y’s : een kolom met waarden voor de responsvariabele
• bekende_x’s : een of meer kolommen met waarden voor de voorspellende variabelen

De volgende voorbeelden laten zien hoe u deze functie kunt gebruiken om een regressievergelijking te vinden voor een eenvoudig lineair regressiemodel en een meervoudig lineair regressiemodel .

Voorbeeld 1: Zoek de vergelijking voor een eenvoudige lineaire regressie

Stel dat we de volgende gegevensset hebben die een voorspellende variabele (x) en een responsvariabele (y) bevat:

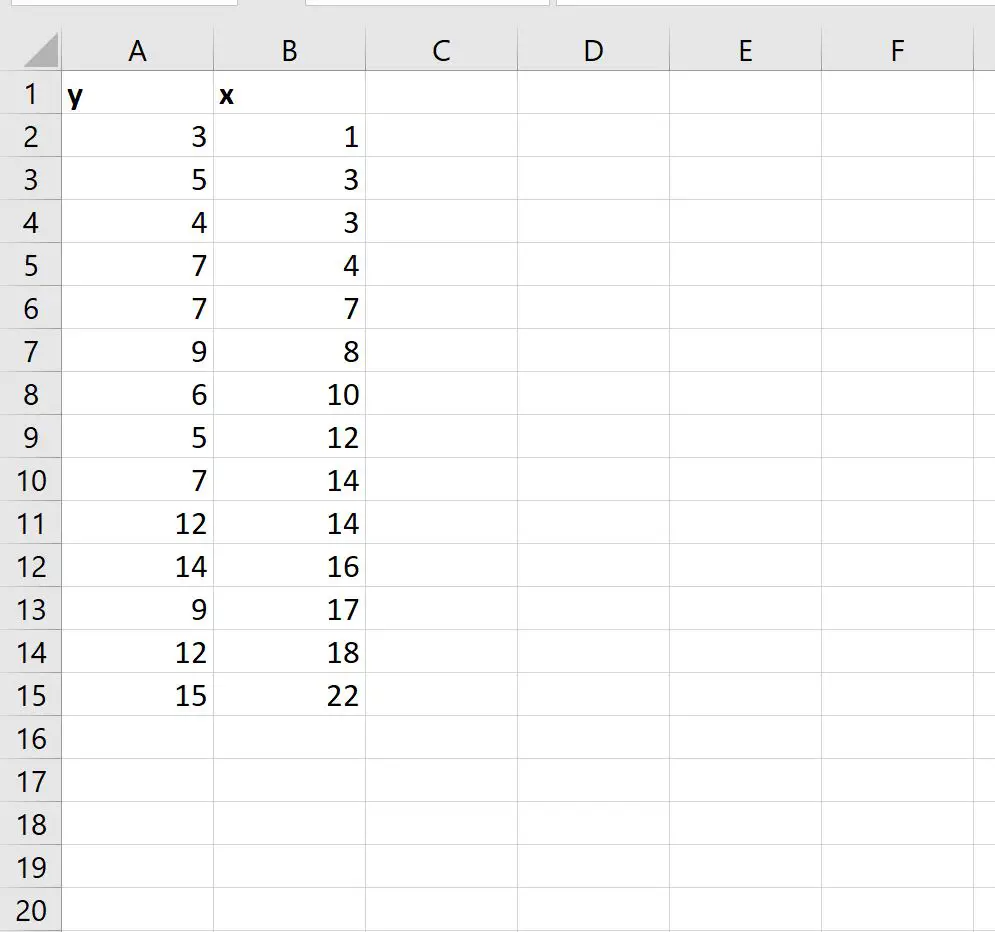
We kunnen de volgende formule in cel D1 typen om de eenvoudige lineaire regressievergelijking voor deze gegevensset te berekenen:

 =LINEST( A2:A15 , B2:B15 )

Zodra we op ENTER drukken, worden de coëfficiënten van het eenvoudige lineaire regressiemodel weergegeven:

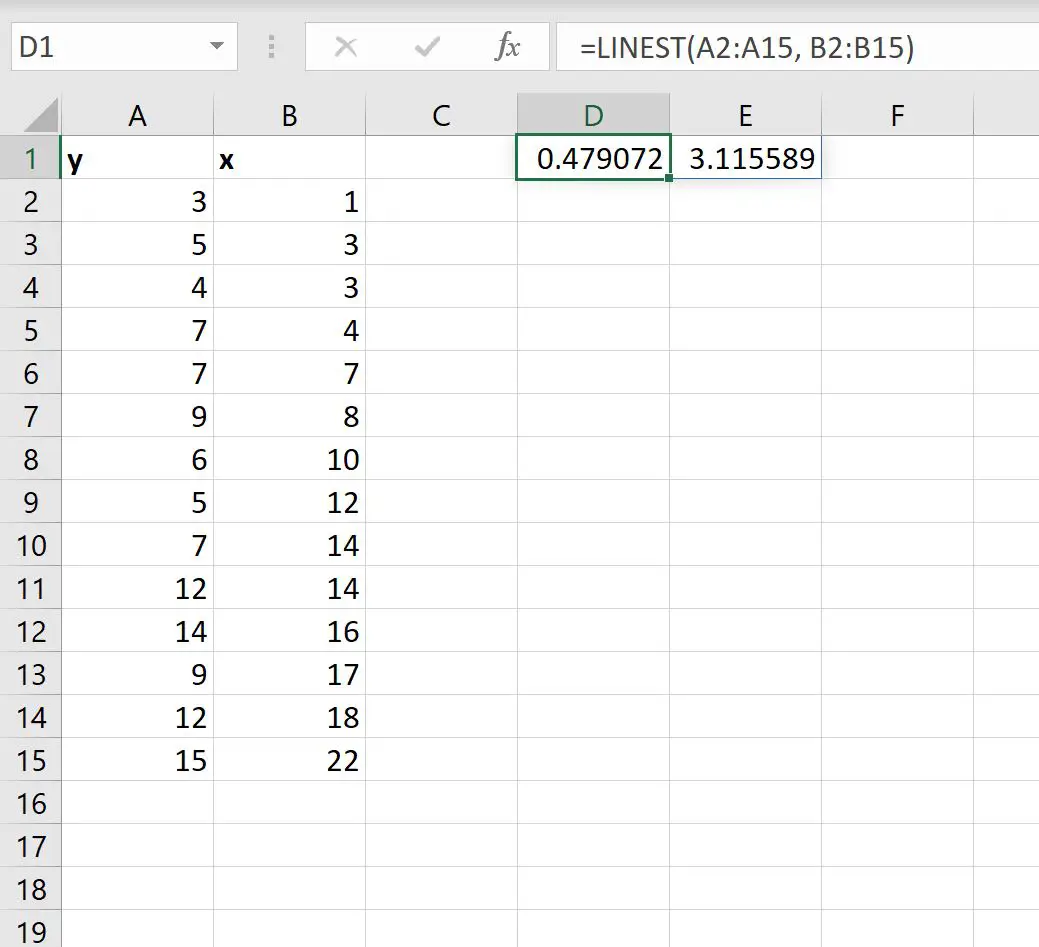
Zo interpreteert u het resultaat:

• De coëfficiënt van het snijpunt is 3,115589
• De hellingscoëfficiënt is 0,479072

Met behulp van deze waarden kunnen we de vergelijking voor dit eenvoudige regressiemodel schrijven:

y = 3,115589 + 0,478072(x)

Opmerking : om p-waarden te vinden voor coëfficiënten, de r-kwadraatwaarde van het model en andere metingen, moet u de regressiefunctie in de Data Analysis ToolPak gebruiken. In deze tutorial wordt uitgelegd hoe u dit moet doen.

Voorbeeld 2: De vergelijking vinden voor meervoudige lineaire regressie

Stel dat we de volgende gegevensset hebben die twee voorspellende variabelen (x1 en x2) en één responsvariabele (y) bevat:

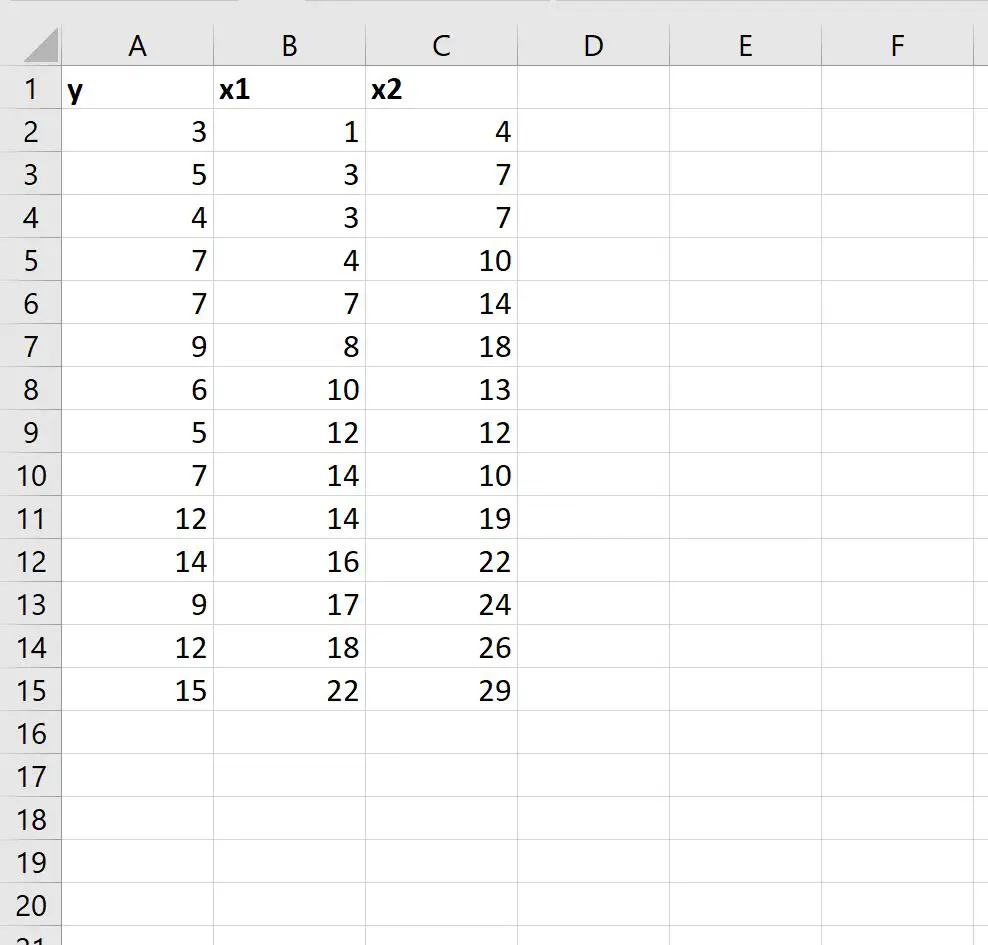
We kunnen de volgende formule in cel E1 typen om de meervoudige lineaire regressievergelijking voor deze gegevensset te berekenen:

 =LINEST( A2:A15 , B2:C15 )

Zodra we op ENTER drukken, worden de coëfficiënten van het meervoudige lineaire regressiemodel weergegeven:

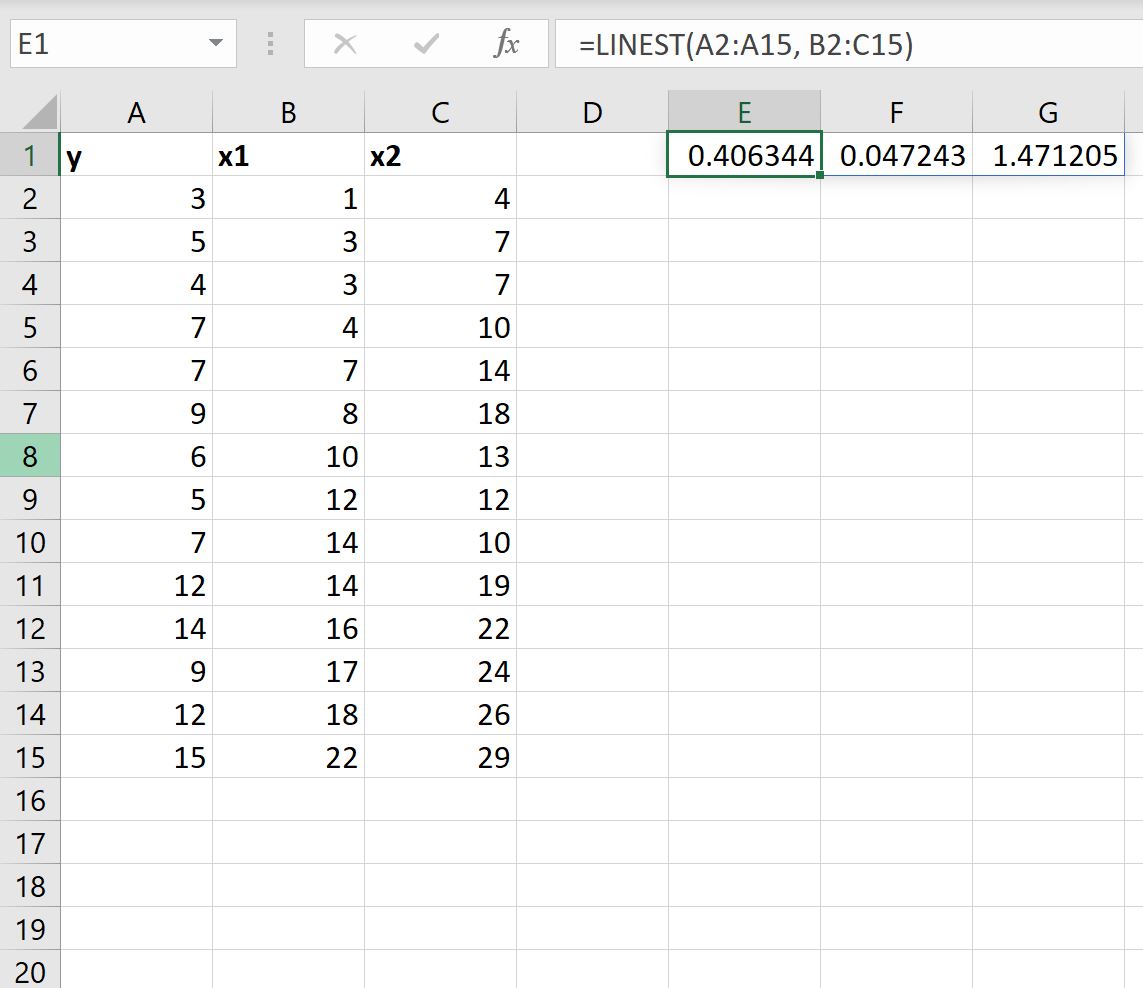
Zo interpreteert u het resultaat:

• De coëfficiënt van het snijpunt is 1,471205
• De coëfficiënt voor x1 is 0,047243
• De coëfficiënt voor x2 is 0,406344

Met behulp van deze waarden kunnen we de vergelijking voor dit meervoudige regressiemodel schrijven:

y = 1,471205 + 0,047243(x1) + 0,406344(x2)

Opmerking : om p-waarden voor coëfficiënten, de r-kwadraatwaarde van het model en andere metingen voor een meervoudig lineair regressiemodel in Excel te vinden, moet u de regressiefunctie in de Data Analysis ToolPak gebruiken. In deze tutorial wordt uitgelegd hoe u dit moet doen.

Aanvullende bronnen

De volgende zelfstudies bieden aanvullende informatie over regressie in Excel:

Hoe regressie-uitvoer in Excel te interpreteren
Hoe u een regressielijn toevoegt aan een spreidingsdiagram in Excel
Hoe polynomiale regressie uit te voeren in Excel