Poissonverdeling of normale verdeling: wat is het verschil?

De Poissonverdeling en de normale verdeling zijn twee van de meest gebruikte kansverdelingen in de statistiek.

Deze tutorial biedt een korte uitleg van elke distributie, evenals twee belangrijke verschillen tussen de distributies.

Een overzicht: de Poissonverdeling

De Poisson-verdeling beschrijft de waarschijnlijkheid van het behalen van k successen gedurende een bepaald tijdsinterval.

Als een willekeurige variabele X een Poisson-verdeling volgt, kan de kans dat X = k succes wordt gevonden met de volgende formule:

P(X=k) = λ ^k * e ^{– λ} / k!

Goud:

• λ: gemiddeld aantal successen dat optreedt tijdens een specifiek interval
• k: aantal successen
• e: een constante gelijk aan ongeveer 2,71828

Stel bijvoorbeeld dat in een bepaald ziekenhuis gemiddeld twee geboorten per uur plaatsvinden. We kunnen de bovenstaande formule gebruiken om de kans te bepalen op 3 geboorten in een bepaald uur:

P(X=3) = 2 ³ * e ^{– 2} / 3! = 0,1805

De kans op drie geboorten in een bepaald uur is 0,1805 .

Een overzicht: de normale verdeling

De normale verdeling beschrijft de waarschijnlijkheid dat een willekeurige variabele in een bepaald interval een waarde aanneemt.

De kansdichtheidsfunctie van een normale verdeling kan worden geschreven als:

P(X=x) = (1/σ√ 2π )e ^{-1/2((x-μ)/σ) 2}

Goud:

• σ: Standaardafwijking van de verdeling
• μ: gemiddelde van de verdeling
• x: waarde van de willekeurige variabele

Stel bijvoorbeeld dat het gewicht van een bepaalde ottersoort normaal verdeeld is met μ = 40 pond en σ = 5 pond.

Als we willekeurig een otter uit deze populatie selecteren, kunnen we de volgende formule gebruiken om de waarschijnlijkheid te bepalen dat deze tussen de 38 en 42 pond weegt:

P ( ^{38 < /5) 2} = 0,3108

De kans dat de willekeurig geselecteerde otter tussen de 38 en 42 pond weegt, is 0,3108 .

Verschil #1: Discreet vs. Continue gegevens

Het eerste verschil tussen de Poisson-verdeling en de normale verdeling is het type gegevens dat door elke waarschijnlijkheidsverdeling wordt gemodelleerd.

Een Poisson-verdeling wordt gebruikt bij het werken met discrete gegevens die alleen gehele waarden gelijk aan of groter dan nul kunnen aannemen. Hier zijn enkele voorbeelden:

• Aantal ontvangen oproepen per uur in een callcenter
• Aantal klanten per dag in een restaurant
• Aantal auto-ongelukken per maand

In elk scenario kan de willekeurige variabele alleen de waarde 0, 1, 2, 3, enz. aannemen.

Bij het werken met continue gegevens wordt een normale verdeling gebruikt die elke waarde kan aannemen, van negatief oneindig tot positief oneindig. Hier zijn enkele voorbeelden:

• Gewicht van een bepaald dier
• Hoogte van een bepaalde plant
• Marathontijden dames
• Temperatuur in Celsius

In deze scenario’s kunnen willekeurige variabelen elke waarde aannemen, zoals -11,3, 21,343435, 85, enz.

Verschil #2: vorm van distributies

Het tweede verschil tussen de Poisson-verdeling en de normale verdeling zit in de vorm van de verdelingen.

Een normale verdeling heeft altijd een belvorm:

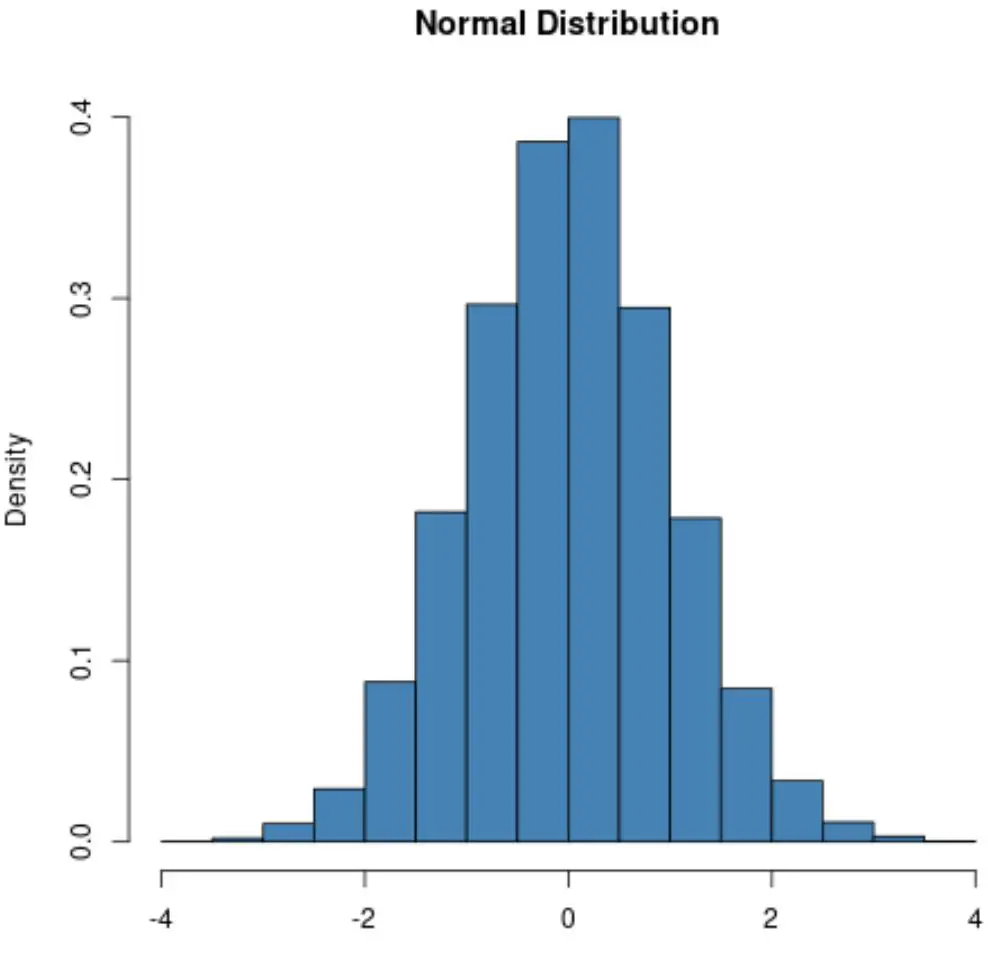
De vorm van de Poisson-verdeling varieert echter afhankelijk van de gemiddelde waarde van de verdeling.

Een Poisson-verdeling met een kleine waarde voor het gemiddelde, zoals μ = 3, zal bijvoorbeeld sterknaar rechts scheef zijn:

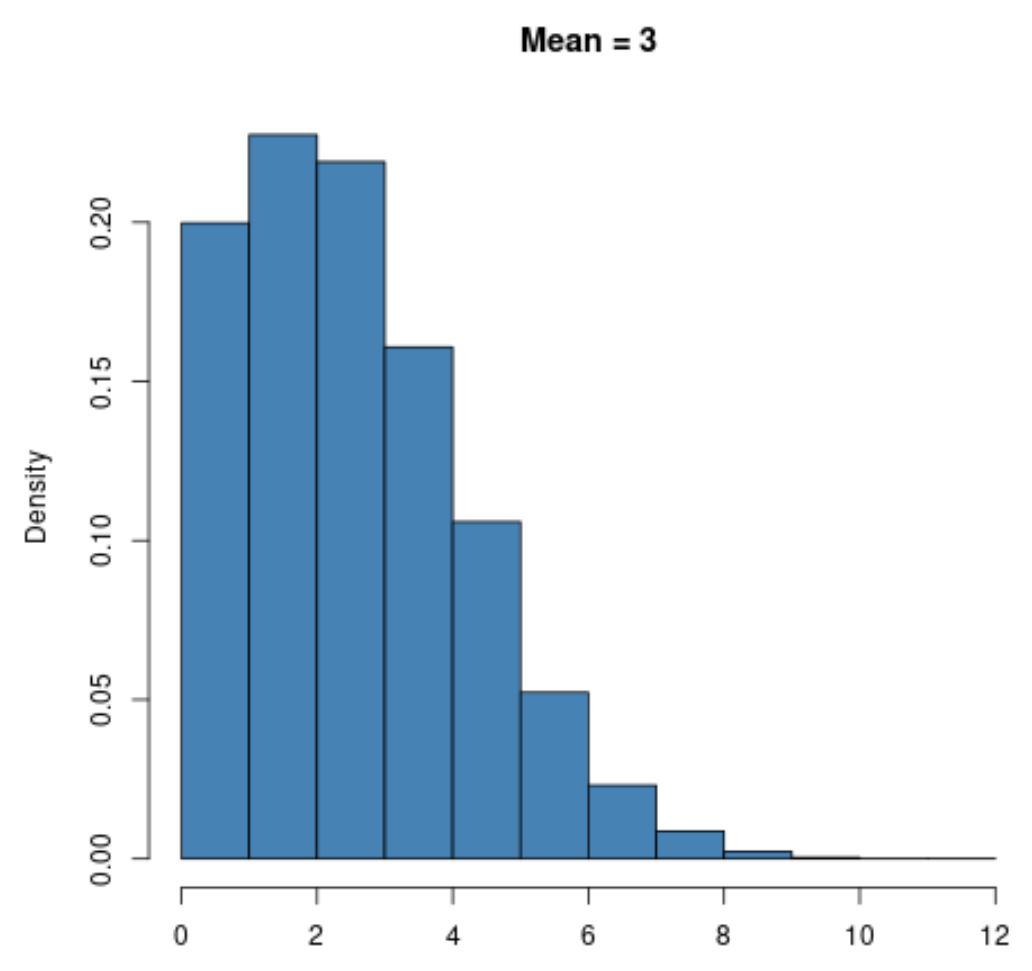
Een Poisson-verdeling met een grotere gemiddelde waarde zoals μ = 20 zal echter een klokvorm vertonen, net als de normale verdeling:

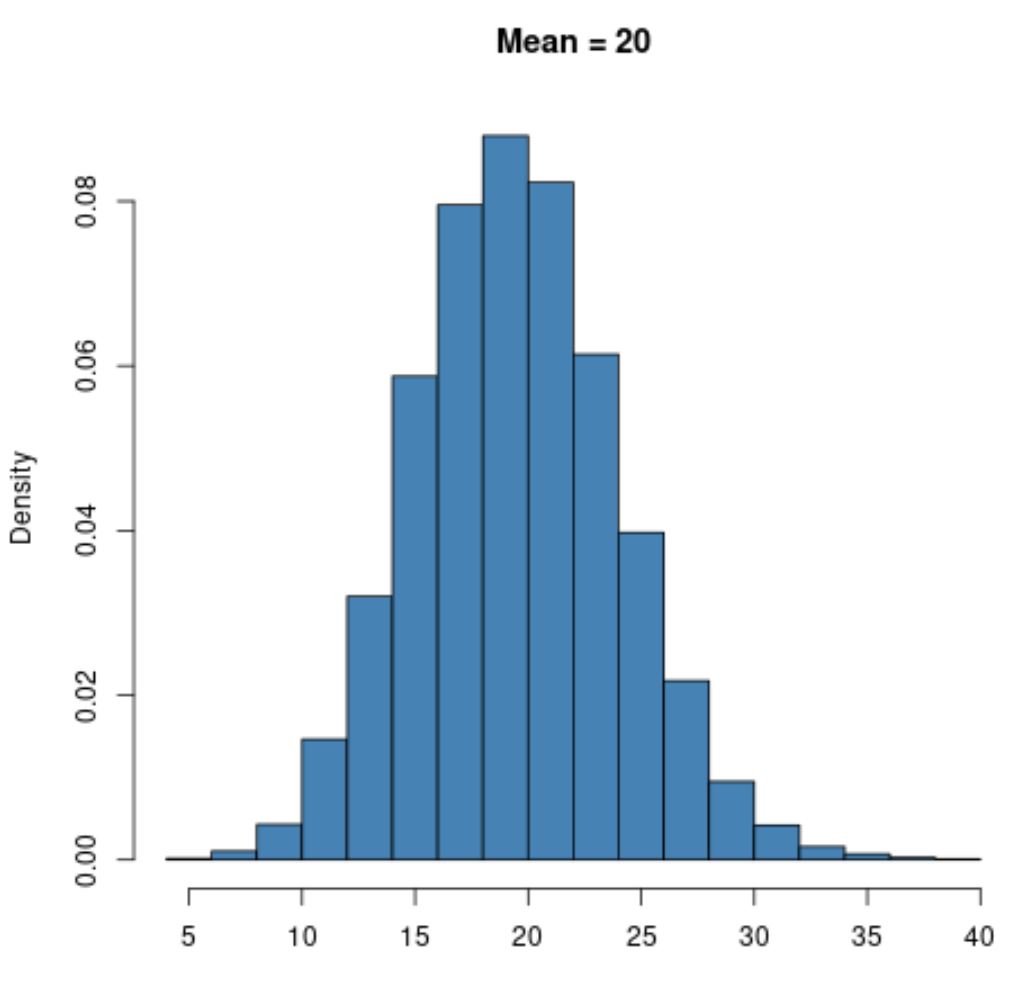
Merk op dat de ondergrens van een Poisson-verdeling altijd nul zal zijn, ongeacht de waarde van het gemiddelde, omdat een Poisson-verdeling alleen kan worden gebruikt met gehele waarden gelijk aan of groter dan nul.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over de Poisson-verdeling:

Een inleiding tot de Poisson-verdeling
De vier hypothesen van de Poisson-verdeling
5 concrete voorbeelden van de Poisson-verdeling

De volgende tutorials bieden aanvullende informatie over de normale verdeling:

Een inleiding tot de normale verdeling
6 concrete voorbeelden van de normale verdeling
Normale verdelingsgegevenssetgenerator