Hoe de poisson-distributie in python te gebruiken

De Poisson-verdeling beschrijft de waarschijnlijkheid van het behalen van k successen gedurende een bepaald tijdsinterval.

Als een willekeurige variabele X een Poisson-verdeling volgt, kan de kans dat X = k succes wordt gevonden met de volgende formule:

P(X=k) = λ ^k * e ^{– λ} / k!

Goud:

• λ: gemiddeld aantal successen dat optreedt tijdens een specifiek interval
• k: aantal successen
• e: een constante gelijk aan ongeveer 2,71828

In deze tutorial wordt uitgelegd hoe u de Poisson-distributie in Python gebruikt.

Hoe een Poisson-verdeling te genereren

U kunt de functie Poisson.rvs(mu, size) gebruiken om willekeurige waarden te genereren uit een Poisson-verdeling met een specifieke gemiddelde waarde en steekproefomvang:

 from scipy. stats import fish

#generate random values from Poisson distribution with mean=3 and sample size=10
fish. rvs (mu=3, size=10)

array([2, 2, 2, 0, 7, 2, 1, 2, 5, 5])

Hoe kansen te berekenen met behulp van een Poisson-verdeling

U kunt de functies Poisson.pmf(k, mu) en Poisson.cdf(k, mu) gebruiken om kansen te berekenen die verband houden met de Poisson-verdeling.

Voorbeeld 1: Waarschijnlijkheid gelijk aan een bepaalde waarde

Een winkel verkoopt gemiddeld 3 appels per dag. Hoe groot is de kans dat ze op een bepaalde dag vijf appels verkopen?

 from scipy. stats import fish

#calculate probability
fish. pmf (k=5, mu=3)

0.100819

De kans dat de winkel op een bepaalde dag 5 appels verkoopt, is 0,100819 .

Voorbeeld 2: Waarschijnlijkheid kleiner dan een bepaalde waarde

Een bepaalde winkel verkoopt gemiddeld zeven voetballen per dag. Wat is de kans dat deze winkel op een bepaalde dag vier of minder voetballen verkoopt?

 from scipy. stats import fish

#calculate probability
fish. cdf (k=4, mu=7)

0.172992

De kans dat de winkel op een bepaalde dag vier of minder voetballen verkoopt, is 0,172992 .

Voorbeeld 3: Waarschijnlijkheid groter dan een bepaalde waarde

Een bepaalde winkel verkoopt gemiddeld 15 blikjes tonijn per dag. Hoe groot is de kans dat deze winkel op een bepaalde dag meer dan twintig blikjes tonijn verkoopt?

 from scipy. stats import fish

#calculate probability
1-fish. cdf (k=20, mu=15)

0.082971

De kans dat de winkel op een bepaalde dag meer dan 20 blikjes tonijn verkoopt, is 0,082971 .

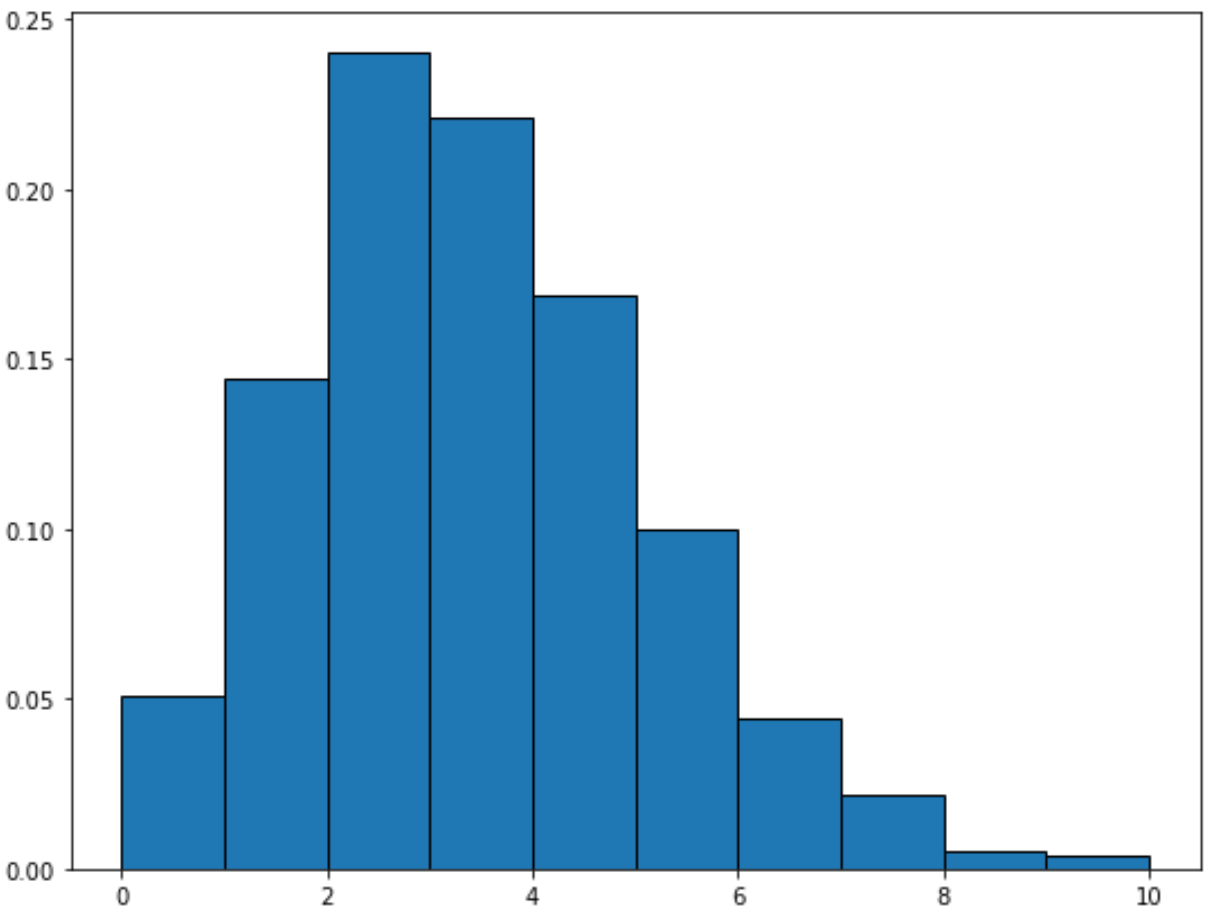
Hoe een Poisson-verdeling te plotten

U kunt de volgende syntaxis gebruiken om een Poisson-verdeling met een bepaald gemiddelde te plotten:

 from scipy. stats import fish
import matplotlib. pyplot as plt

#generate Poisson distribution with sample size 10000
x = fish. rvs (mu=3, size=10000)

#create plot of Poisson distribution
plt. hist (x, density= True , edgecolor=' black ')

Aanvullende bronnen

Een inleiding tot de Poisson-verdeling
5 concrete voorbeelden van de Poisson-verdeling
Online visverspreidingscalculator