Wat is een voedseltest? (uitleg & voorbeeld)

Een Chow-test is een statistische test ontwikkeld door econoom Gregory Chow die wordt gebruikt om te testen of de coëfficiënten van twee verschillende regressiemodellen op verschillende datasets gelijk zijn.

De Chow-test wordt doorgaans gebruikt op het gebied van de econometrie met tijdreeksgegevens om te bepalen of er op een bepaald moment een structurele breuk in de gegevens is.

Beschouw bijvoorbeeld het volgende spreidingsdiagram:

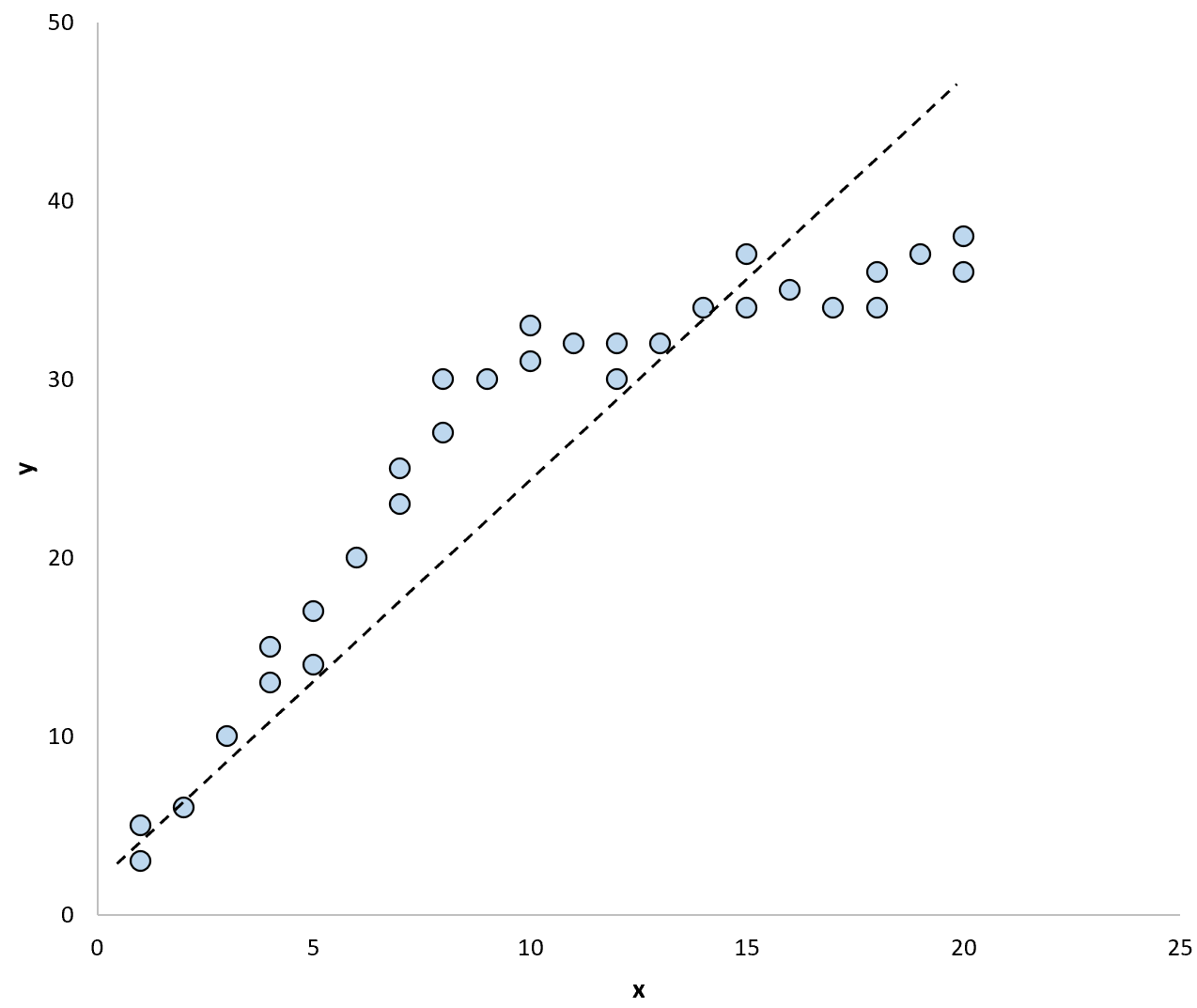
Als we een regressielijn zouden gebruiken om het model in de gegevens samen te vatten, zou het er als volgt uit kunnen zien:

En als we twee afzonderlijke regressielijnen zouden gebruiken om het model in de gegevens samen te vatten, zou het er als volgt uit kunnen zien:

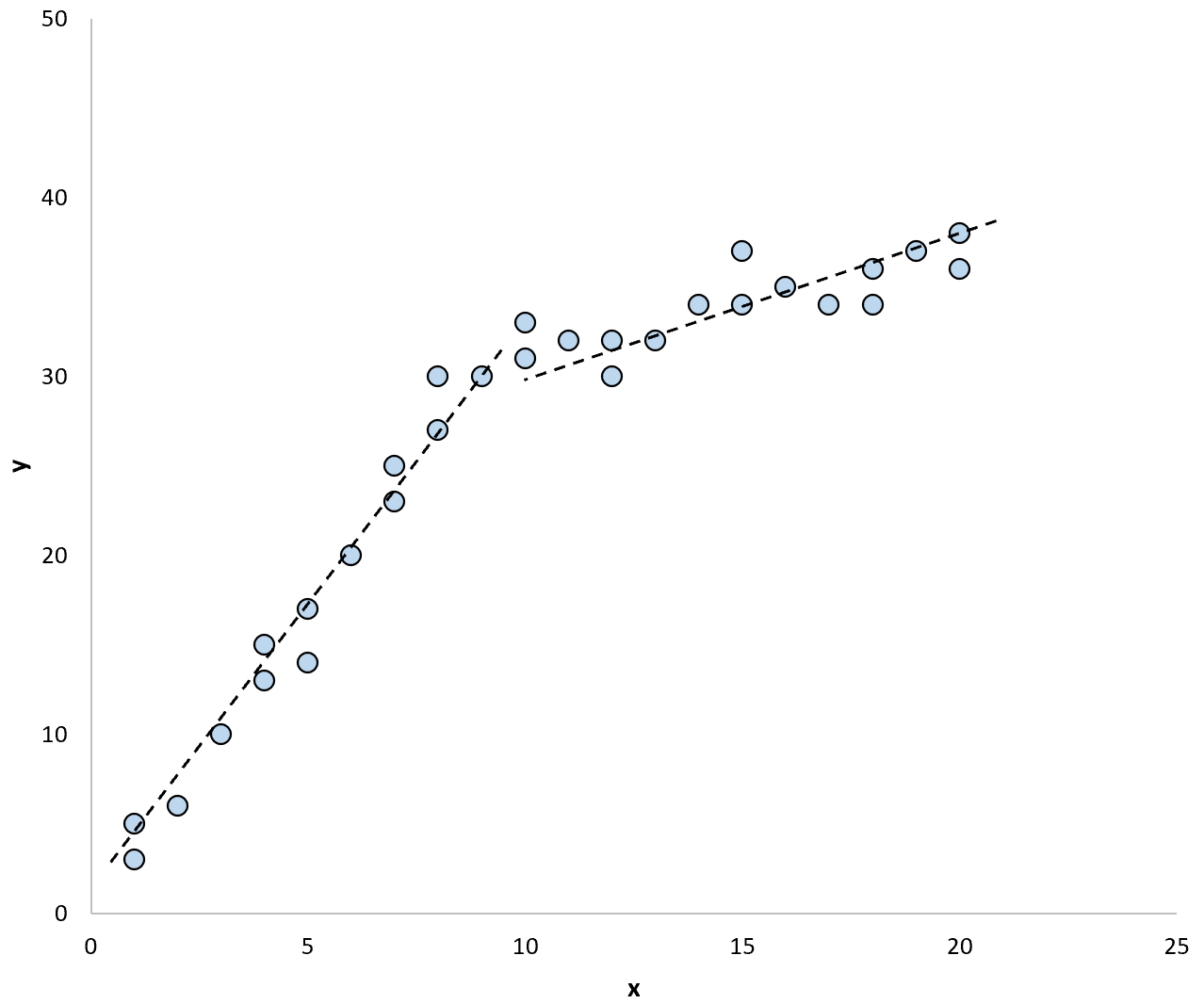
Met de Chow-test kunnen we testen of de regressiecoëfficiënten van elke regressielijn gelijk zijn of niet.

Als uit de test blijkt dat de coëfficiënten tussen de regressielijnen niet gelijk zijn, betekent dit dat er significant bewijs is van een structurele breuk in de gegevens. Met andere woorden: de gegevenstrend is vóór en na dit structurele breekpunt heel verschillend.

Wanneer moet u de Chow-test gebruiken?

De volgende voorbeelden illustreren situaties waarin u mogelijk een Chow-test wilt uitvoeren:

1. Bepaal of de aandelenkoersen vóór en na verkiezingen met verschillende snelheden bewegen.

2. Bepaal of de huizenprijzen voor en na een rentewijziging veranderen.

3. Bepaal of de gemiddelde winst van overheidsbedrijven verschilt voor en na de goedkeuring van een nieuwe belastingwet.

In elke situatie kunnen we een Chow-test gebruiken om te bepalen of er op een bepaald moment een structureel breekpunt in de gegevens zit.

Stappen om een Chow-test uit te voeren

We kunnen de volgende stappen gebruiken om een Chow-test uit te voeren.

Stap 1: Definieer de nul- en alternatieve hypothesen.

Stel dat we het volgende regressiemodel passen op onze gehele dataset:

• y _t = a + bx _1t + cx _t2 + ε

Stel vervolgens dat we onze gegevens in twee groepen verdelen op basis van een structureel breekpunt en de volgende regressiemodellen voor elke groep passen:

• y _t = a ₁ + b ₁ x _1t + c ₁ x _t2 + ε
• y _t = a ₂ + b ₂ x _1t + c ₂ x _t2 + ε

We zouden de volgende nul- en alternatieve hypothesen gebruiken voor de Chow-test:

• Nul (H ₀ ): a ₁ = a ₂ , b ₁ = b ₂ en c ₁ = c ₂
• Alternatief ( _HA ): Minstens één van de vergelijkingen in Null is niet gelijk.

Als we de nulhypothese verwerpen, hebben we voldoende bewijs om te zeggen dat er een structureel breekpunt in de gegevens zit en dat twee regressielijnen beter bij de gegevens passen dan één.

Als we er niet in slagen de nulhypothese te verwerpen, hebben we niet genoeg bewijs om te zeggen dat er een structureel breekpunt in de gegevens zit. In dit geval zeggen we dat de regressielijnen kunnen worden samengevoegd tot één enkele regressielijn die het patroon van de gegevens goed genoeg weergeeft.

Stap 2: Bereken de teststatistiek.

Als we de volgende termen definiëren:

• _ST : De som van de kwadraten van de residuen van de totale gegevens
• S ₁ , S ₂ : de som van de kwadraten van de residuen van elke groep
• N ₁ , N ₂ : Het aantal waarnemingen in elke groep
• k: het aantal parameters

We kunnen dan zeggen dat de Chow-teststatistiek is:

Chow-teststatistiek = [(S _T – (S ₁ +S ₂ ))/k] / [(S ₁ +S ₂ )/ (N ₁ +N ₂ -2k)]

Deze teststatistiek volgt de F-verdeling met k en en N ₁ +N ₂ -2k vrijheidsgraden.

Stap 3: Verwerp de nulhypothese of verwerp deze niet.

Als de p-waarde die aan deze teststatistiek is gekoppeld onder een bepaald significantieniveau ligt, kunnen we de nulhypothese verwerpen en concluderen dat er een structureel breekpunt in de gegevens zit.

Gelukkig is de meeste statistische software in staat een Chow-test uit te voeren, zodat u de test waarschijnlijk nooit handmatig hoeft uit te voeren.

Voorbeeld van het uitvoeren van een Chow-test

Raadpleeg deze tutorial voor een stapsgewijs voorbeeld van hoe u een Chow-test uitvoert voor een bepaalde dataset in R.

Chow-testnotities

Hier zijn enkele opmerkingen waarmee u rekening moet houden bij de Chow-test:

1. Bij de test wordt ervan uitgegaan dat de residuen van de regressiemodellen onafhankelijk en identiek verdeeld zijn vanuit een normale verdeling met onbekende variantie.

2. De Chow-test mag alleen worden gebruikt als de structurele breuk die u wilt testen zich op een bekend tijdstip voordoet. Met andere woorden: de test mag niet herhaaldelijk worden gebruikt om te bepalen of een bepaald moment als een structurele breuk kan worden beschouwd.